
- •Лекция 1 Введение
- •Структура курса
- •Учебники
- •Задачники
- •Раздел 1. Алгебра и геометрия.
- •Тема 1.1. Определители.
- •Лекция 2.
- •Тема 1.2. Матрицы.
- •1.2.1.Понятие матрицы.
- •1.2.2.Операции с матрицами.
- •Лекция 3
- •Тема 1.3. Обратная матрица.
- •1.3.1.Понятие обратной матрицы.
- •Если матрица а имеет обратную матрицу а-1, то она единственная.
- •1.3.2. Получение обратной матрицы с помощью присоединенной матрицы.
- •1.3.3. Получение обратной матрицы методом элементарных преобразований.
- •Тема 1.4. Система линейных алгебраических уравнений (слау)
- •1.4.1.Решение слау методом Крамера.
- •1.4.2. Решение слау методом Гаусса
- •1.4.3 Решение слау с помощью обратной матрицы
- •Тема 1.5. Однородные, неопределённые и несовместные системы линейных алгебраических уравнений (слау)
- •1.5.1. Решение однородных слау.
- •1.5.2.Решение неопределённых слау.
- •1.5.3. Определение несовместных слау.
- •Лекция 6
- •1.6. Векторная алгебра
- •1.4.1. Вектор. Линейные операции с векторами. Базис. Декартова система координат (дск).
- •1.6.2. Скалярное, векторное и смешанное произведение векторов.
- •1.4.3 Преобразование координат. Полярная система
- •Переход из пск в дск и из дск в пск
- •Лекция 7
- •1.7 Аналитическая геометрия
- •1.7.1 Аналитическая геометрия на плоскости. Уравнение прямой линии на плоскости.
- •1.7.2 Кривые второго порядка в декартовой системе координат.
- •1.7.3. Кривые второго порядка в полярной системе координат.
- •Лекция 8
- •1.8 Аналитическая геометрия в пространстве.
- •1.8.1 . Уравнение плоскости в пространстве.
- •4) Условия параллельности и перпендикулярности плоскостей.
- •1.8.2. Уравнение прямой линии в пространстве.
- •1.8.3. Поверхности 2-го порядка.
- •Раздел 2. Дифференциальное исчисление.
- •Тема 2.1. Введение в анализ.
- •2.1.1. Действительные числа. Абсолютная величина действительного числа. Постоянные и переменные величины.
- •3) Свойства абсолютной величины.
- •2.1.3. Предел функции. Основные теоремы о пределах.
- •4) Основные теоремы о пределах.
- •Тема 2.2. Предел и непрерывность функции.
- •2.2.1. Первый и второй замечательные приделы. Раскрытие неопределённостей типа .
- •2.2.2. Непрерывность функции.
- •2.2.3. Бесконечно малые функции и бесконечно большие функции.
- •Тема 2.3. Производные функции одной переменной.
- •Тема 2.4. Дифференциал.
- •Тема 2.5. Основные теоремы о дифференцируемых функциях.
- •Тема 2.6. Некоторые сведения из высшей алгебры.
- •2.6.2. Теоремы Гаусса и Безу.
- •2.6.3. Разложение алгебраических многочленов на множители.
- •Модуль 3. Интегральное исчисление.
- •Тема 3.1. Неопределенный интеграл.
- •3.1.1. Первообразная и неопределенный интеграл.
- •3.1.2. Свойства неопределенного интеграла и таблица интегралов.
- •3.1.3. Методы интегрирования
- •Тема 3.2. Интегрирование рациональных и тригонометрических функций.
- •3.2.1. Интегрирование рациональных дробей.
- •3.2.2. Интегрирование иррациональных функций.
- •3.2.3. Интегрирование тригонометрических функций.
- •Тема 3.3. Определенный интеграл.
- •3.3.1. Определенный интеграл. Теорема существования. Основные свойства определенного интеграла.
- •3.3.2. Формула Ньютона – Лейбница.
2.6.2. Теоремы Гаусса и Безу.
1) Теорема Гаусса.
Алгебраическое уравнение вида:
 ,
(2.6.10.)
,
(2.6.10.)
где
ai
– действительные или комплексные числа,
имеет, по крайней мере, один действительный
или комплексный корень
 .
.
Выражение вида:
 (2.6.11.)
(2.6.11.)
называется
однородным алгебраическим полиномом
п-ой
степени. Если при подстановке в него
вместо х значения
 он обращается в ноль, то
он обращается в ноль, то считается корнем данного полинома.
считается корнем данного полинома.
2) Теорема Безу.
Если
 -
корень полинома (2.6.11.), то этот полином
делится без остатка на выражение ( х -
-
корень полинома (2.6.11.), то этот полином
делится без остатка на выражение ( х - ).
).
2.6.3. Разложение алгебраических многочленов на множители.
Пример.
Разложить на элементарные множители полином вида
![]()
Решение
![]() .
На основании теоремы Гаусса у этого
уравнения имеется по крайней мере один
действительный корень, подбором
определяем его:
.
На основании теоремы Гаусса у этого
уравнения имеется по крайней мере один
действительный корень, подбором
определяем его:
![]()
(Проверка:
![]() )
)
Согласно
теореме Безу полином
![]() должен без остатка разделиться на
должен без остатка разделиться на :
:
![]()

![]()
![]()
![]()
![]()
![]()
![]()
Затем определяются остальные корни
![]()

Ответ:
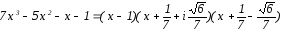
Лекция 15.
Модуль 3. Интегральное исчисление.
Тема 3.1. Неопределенный интеграл.
3.1.1. Первообразная и неопределенный интеграл.
3.1.2. Свойства неопределенного интеграла и таблица интегралов.
3.1.3. Методы интегрирования.
3.1.1. Первообразная и неопределенный интеграл.
1) Первообразная.
Функция F(x) называется первообразной от функции f(x) на отрезке [a,b], если во всех точках этого отрезка F`(x) = f (x) (3.1.1.)
Если F1(x) и F2(x)– две первообразные от функции f (x) на отрезке [a,b], то разность между ними равна постоянному числу, т.е.
F1(x) – F2(x) = c = const (3.1.2)
2) Неопределенный интеграл
Если F(x) первообразная для f (x), то F(x) + c называется неопределенным интегралом: ∫ f(x) dx = F( x) + c (3.1.3.)
3.1.2. Свойства неопределенного интеграла и таблица интегралов.
Свойства неопределенного интеграла
( ∫ f(x) dx)` = ( F(x) + c)` = f(x)
d ∫ f(x) dx = f(x) dx
∫ d F(x) = F(x) + c
∫ (f1(x) + f2(x)) dx = ∫ f1(x) dx + ∫ f2(x) dx
∫ a f(x) dx = a ∫ f(x) dx
∫ f(ax) dx =
 F(ax) + c
F(ax) + c∫ f (x+b) dx = F (x+b) + c
∫ f (ax+b) dx =
 F (ax+b) + c
F (ax+b) + c
2) Таблица интегралов
∫ dx = x+c, 2. ∫ c f(x) dx = c ∫ f(x) dx, 3. ∫ x dx =
 +
c, 4. ∫
+
c, 4. ∫ = ln \x\ +c,
= ln \x\ +c,
5.
∫ aх
dx = +c,
6. ∫ eх
dx = eх
+c,7. ∫ logа
x dx =
+c,
6. ∫ eх
dx = eх
+c,7. ∫ logа
x dx =
 ,
,
8. ∫ ln xdx= x(ln x – 1)+c, 9. ∫ sin xdx = -cos x +c, 10. ∫ cos xdx = sin x+c,
∫ tgx dx = - ln
 +c,
12. ∫ ctgx dx = ln
+c,
12. ∫ ctgx dx = ln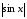 +
c
+
c
13.
∫ arc sin xdx = x arcsin x +
 + c
+ c
∫ arc cos xdx = x arc cos x +
 +
c
+
c∫ arc tg xdx = x arc tg x –
 ln (1+x²) + c,
ln (1+x²) + c,∫ arc ctg xdx = x arc ctg x –
 ln (1+x²) + c,
ln (1+x²) + c,∫ sh xdx = chx + c, 18. ∫ ch xdx = sh x + c,
19.
∫ dx
=
arc sin x + c = -arc cos x + c,
dx
=
arc sin x + c = -arc cos x + c,
20.
∫ dx
=
arc sin x + c = -arc cos x + c,
dx
=
arc sin x + c = -arc cos x + c,
21.
∫ dx = arc sin
dx = arc sin + c = - arc cos
+ c = - arc cos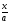 + c,
+ c,
22.
 ,
23.
,
23. ,
,
24.
 25.
25.
26.
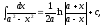 27.
27.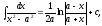
28.
 29.
29. 30.
30.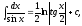
31.
 32.
∫ (u+v) dx = ∫ udx + ∫ vdx, 33.∫
udv
= uv
- ∫ vdu
32.
∫ (u+v) dx = ∫ udx + ∫ vdx, 33.∫
udv
= uv
- ∫ vdu
Пример
Пользуясь таблицей основных интегралов, найти неопределенный интеграл
∫(5х+1)2dx = ∫(25х2 +10х +1)dх = ∫ 25х2dx +∫ 10х dх +∫ 1dх =25 ∫ х2dx +10 ∫ х dx + ∫ dх =

