Тема 2.6. Некоторые сведения из высшей алгебры.

2.6.1. Комплексные числа и уравнения.

2.6.2. Теоремы Гаусса и Безу.

2.6.3. Разложение алгебраических многочленов на множители.

2.6.1. Комплексные числа и уравнения.

1. Понятие комплексного числа.

Комплексным числом называется выражение вида

z = a + ib,(2.6.1.)

в котором a, b– действительные числа, ai = (i² = -1)- мнимое число (мнимая единица).

2. Свойства комплексного числа.

(1) Если z₁= a₁+ib₁, z₂ =a₂+ib₂, то z₁= z₂ в том случае, когдаa₁ = a₂, b₁ = b₂

(2) z₁z₂ = (a₁ a₂) + i(b₁b₂).

(3) z = a + i(b)

(4) z₁ z₂ = (a₁ + ib₁)(a₂ + ib₂) = (a₁ a₂ – b₁ b₂) + i(a₁ b₂ + a₂ b₁), (a +ib)(a - ib) = a² + b²

5. 

3) Комплексные числа в тригонометрической форме.

z = a + ib = r (cos + i sin  )

1. z₁ + z₂ = (r₁ cos ₁ + r₂ cos  ₂) + i (r₁ sin ₁ + r₂ sin  ₂)

2) z₁ * z₂ = r₁ (cos ₁ +i sin ₁) * r₂ (cos ₂ + i sin ₂) =

=r₁ r₂ (cos ₁ cos ₂ + i cos ₁ sin ₂ + sin ₁ cos ₂ + i ² sin ₁ sin ₂) =

=r₁ r₂ [ (cos ₁ cos ₂ – sin ₁ sin ₂) + i (cos ₁ sin ₂ + sin ₁ cos ₂)] =

=r₁ r₂ [ cos (₁ + ₂)+ i sin (₁ + ₂)]

2. Формула Муавра.

z = r (cos + i sin )

zⁿ=[r(cos+isin)]ⁿ=rⁿ(cosn +i sinn) (2.6.2)

(2.6.3)

Типовой пример.

(cos + i sin)³ = cos3 + i sin3

(cos + i sin)³ = cos³ +i 3cos² sin + i ² 3cos sin² + i ³ sin³ = (cos³ – 3 cos sin²) +i (3 cos² sin – sin³) = cos 3 + i sin3.

cos3 = cos³ – 3cos sin²

Sin3 = 3 cos² sin – sin³

4) Комплексные числа в показательной форме. Формулы Эйлера.

сos + i sin = ℯ ^i (2.6.4.)

cos – i sin = ℯ ^-i (2.6.5.)

z= r (cos + i sin)=ℯ^+i , (2.6.6.)

где r=ℯ ^, cos + i sin = ℯ^i (2.6.7.)

z₁ z₂ = (2.6.8.)

z ⁿ = ℯ ^iⁿ ℯ ^nin (2.6.9.)

5) Алгебраические уравнения с комплексными числами.

Типовые примеры.

1. х⁴ + 1 = 0

Решение

x⁴ = -1 = cos (+ 2k) + i sin(+ 2k) = cos(2k + 1)+ i sin(2k + 1)

x^k = cos(2k + 1)+ i sin(2k + 1)

k=0 x₀ = cos + i sin=

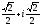
k=1 x₁=cos 3+ i sin 3= -

k=2 x₂=cos 5+ i sin 5= -

k=3 x₃=cos 7+ i sin 7=

2. x² – (2 + i)x + (-1 + 7i) = 0

Решение.

Пусть x = U + i V

(U + i V) ² – (2 + i) (U + I V) + (-1 + 7i) = 0

U² + i2UV +i2 V² – 2U - iU – i2V – i²U – 1 + 7i = 0

U² – V² – 2U + V– 1 = 0 (U -1)² - (V-0,5)² – 1,75 = 0

2 U V – U – 2 V +7 = 0 (U-1)2 (V-0,5) = -6

U – 1 =  ^^    ^  ^  ^  ^    

V – ½ = ,         , U = 1+, V = ½ +,

(^)_  .

(^)_    _  

(^)_  -    _  I

_        _      

_    _   i   

U = 1 +  U _1,2 = 1 2 U₁ = 3, U₂ = -1

U _3,4 = 1  1,5i, U₃ = 1+ 1,5i U₄ = 1 – 1,5,i

V = ½ +  V _{1, 2} = ½  1,5 V₁ = -1, V2 = 2

V_3,4 = ½  2i V₃ = 0,5 + 2i V₄ = 0,5 – 2i

х _i = U_i + V_i

x₁ = U₁ + iV₁ = 3 – i

x₂ = U₂ + iV₂ = -1 +2 i

x₃ = U₃ +iV₃ = 1 + 1,5i + i (0,5 +2i) = -1 + 2i

x₄ = U₄ +iV₄ = 1 – 1,5i + i (0,5 – 2i) = 3 – i

x₁ = x₄ = 3 – i

x₂ = x₃ = -1 + 2i

Проверка.

1) (3-i)² – (2+i)(3-i)–1+7i =0

9-6i+i²-6-3i+2i+i²-1-7i=9-6i-1-6-3i+2i-1-1+7i=(9-1-6-1-1)+(-6i-3i+2i+7i)=

=0+0i=0.

2) (-1+2i)²-(2+i)(-1+2i)-1+7i=0

1-4i+4i²+2-4i+i-2i²-1+7i=1-4i-4+2-4i+i+2-1-7i=(1-4+2+2-1)+(-4i-4i+i+7i)=

=0+0i=0.