
- •Лекция 1 Введение
- •Структура курса
- •Учебники
- •Задачники
- •Раздел 1. Алгебра и геометрия.
- •Тема 1.1. Определители.
- •Лекция 2.
- •Тема 1.2. Матрицы.
- •1.2.1.Понятие матрицы.
- •1.2.2.Операции с матрицами.
- •Лекция 3
- •Тема 1.3. Обратная матрица.
- •1.3.1.Понятие обратной матрицы.
- •Если матрица а имеет обратную матрицу а-1, то она единственная.
- •1.3.2. Получение обратной матрицы с помощью присоединенной матрицы.
- •1.3.3. Получение обратной матрицы методом элементарных преобразований.
- •Тема 1.4. Система линейных алгебраических уравнений (слау)
- •1.4.1.Решение слау методом Крамера.
- •1.4.2. Решение слау методом Гаусса
- •1.4.3 Решение слау с помощью обратной матрицы
- •Тема 1.5. Однородные, неопределённые и несовместные системы линейных алгебраических уравнений (слау)
- •1.5.1. Решение однородных слау.
- •1.5.2.Решение неопределённых слау.
- •1.5.3. Определение несовместных слау.
- •Лекция 6
- •1.6. Векторная алгебра
- •1.4.1. Вектор. Линейные операции с векторами. Базис. Декартова система координат (дск).
- •1.6.2. Скалярное, векторное и смешанное произведение векторов.
- •1.4.3 Преобразование координат. Полярная система
- •Переход из пск в дск и из дск в пск
- •Лекция 7
- •1.7 Аналитическая геометрия
- •1.7.1 Аналитическая геометрия на плоскости. Уравнение прямой линии на плоскости.
- •1.7.2 Кривые второго порядка в декартовой системе координат.
- •1.7.3. Кривые второго порядка в полярной системе координат.
- •Лекция 8
- •1.8 Аналитическая геометрия в пространстве.
- •1.8.1 . Уравнение плоскости в пространстве.
- •4) Условия параллельности и перпендикулярности плоскостей.
- •1.8.2. Уравнение прямой линии в пространстве.
- •1.8.3. Поверхности 2-го порядка.
- •Раздел 2. Дифференциальное исчисление.
- •Тема 2.1. Введение в анализ.
- •2.1.1. Действительные числа. Абсолютная величина действительного числа. Постоянные и переменные величины.
- •3) Свойства абсолютной величины.
- •2.1.3. Предел функции. Основные теоремы о пределах.
- •4) Основные теоремы о пределах.
- •Тема 2.2. Предел и непрерывность функции.
- •2.2.1. Первый и второй замечательные приделы. Раскрытие неопределённостей типа .
- •2.2.2. Непрерывность функции.
- •2.2.3. Бесконечно малые функции и бесконечно большие функции.
- •Тема 2.3. Производные функции одной переменной.
- •Тема 2.4. Дифференциал.
- •Тема 2.5. Основные теоремы о дифференцируемых функциях.
- •Тема 2.6. Некоторые сведения из высшей алгебры.
- •2.6.2. Теоремы Гаусса и Безу.
- •2.6.3. Разложение алгебраических многочленов на множители.
- •Модуль 3. Интегральное исчисление.
- •Тема 3.1. Неопределенный интеграл.
- •3.1.1. Первообразная и неопределенный интеграл.
- •3.1.2. Свойства неопределенного интеграла и таблица интегралов.
- •3.1.3. Методы интегрирования
- •Тема 3.2. Интегрирование рациональных и тригонометрических функций.
- •3.2.1. Интегрирование рациональных дробей.
- •3.2.2. Интегрирование иррациональных функций.
- •3.2.3. Интегрирование тригонометрических функций.
- •Тема 3.3. Определенный интеграл.
- •3.3.1. Определенный интеграл. Теорема существования. Основные свойства определенного интеграла.
- •3.3.2. Формула Ньютона – Лейбница.
Тема 2.4. Дифференциал.
Дифференциал и его геометрический смысл.
Приближенные вычисления с помощью дифференциала.
Производные и дифференциалы различных порядков.
Дифференциал и его геометрический смысл.
Понятие дифференциала.
 ,
,
 - главная часть приращения функции,
- главная часть приращения функции, - б.м.ф. большего порядка малости, чем
главная часть приращения функции.
- б.м.ф. большего порядка малости, чем
главная часть приращения функции.
Дифференциалом функции
у = у(х)называется главная часть
приращения функцииdy=
 x
(2.4.1.)
x
(2.4.1.)
Дифференциал аргумента равен приращению аргумента
dx
= x
(2.4.2.)
x
(2.4.2.)
Геометрический смысл дифференциала.
y
f(x)
K
y dy
M L
x x + x x
Из треугольника MKL: KL = dy = tgx = yx
Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
dy=
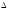 x=
x= (2.4.3.)
(2.4.3.)
Свойства дифференциала.
Если u = u(x) и v = v(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
d(u v) = (u v)dx = udx vdx = du dv
d(uv) = (uv)dx = (uv + vu)dx = vdu + udv
d(Cu) = Cdu
4)Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t),т.е у- сложная функция.
Тогда dy = f(x)g(t)dt = f(x)dx.
Видно, что форма записи дифференциала dyне зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х- независимая переменная, то
dx=x, но если х зависит отt, тохdx.
Таким образом форма записи dy=f(x)xне является инвариантной.
Пример.
Найти производную функции .
.
Решение.
Сначала
преобразуем данную функцию:

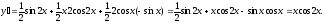
Пример.
Найти производную функции
 .
.
Решение.

Пример.
Найти производную функции

Решение.
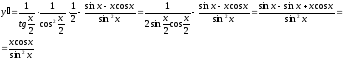
Пример.
Найти производную функции

Решение.
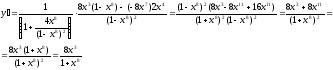
Пример.
Найти производную функции

Решение.
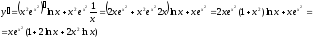
Приближенные вычисления с помощью дифференциалов.
 (2.4.4.)
(2.4.4.)
Пример

Решение
х = 16, х+ х
= 17,
х
= 17, х
= 1
х
= 1
 у(х +
у(х +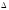 х)у(х) +
х)у(х) +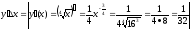 =
=
=
Производные и дифференциалы различных порядков.
Производные различных порядков.
Производной n-го порядка от функцииу = у(х)называется1-я производная от(n-1)-й производной от функцииу = у(х)
у(n) = (y(n-1))’ (2.4.5.)
Некоторые высшие производные.
1)) (СU) (n) = C U (n) (2.4.6.)
2)) (UV) (n) = U (n) V (n) (2.4.7.)
3)) Формула
Лейбница:
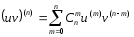 (2.4.8.)
(2.4.8.)
2) Производные различных порядков от функций заданных неявно.
Пример

Производные различных порядков от функций заданных параметрически.
 (2.4.9.)
(2.4.9.)
 (2.4.10.)
(2.4.10.)
Дифференциалы различных порядков.
Дифференциалом n-го порядка от функцииу = у(х)называется дифференциал1-го порядка от дифференциала(n -1)-го порядка от функцииу = у(х).
 (2.4.11.)
(2.4.11.)
 (2.4.12.)
(2.4.12.)
Лекция 13.

