2.1.3. Предел функции. Основные теоремы о пределах.
1)Предел функции в точке.
y(х)
= A
√
> 0
δ
= δ(
)
> 0 |х-х0|<δ|
y(х)–A|<
(2.1.7)
2) Односторонние пределы. Предел слева:
y(х)
= A
√
> 0
δ
= δ(
)>
0x<x0
|х-х0|<δ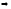
|
y(х)–A|<
(2.1.8)
Аналогично определяется
предел функции справа:
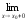y(х) = A. Предел слева и предел
справа – односторонние пределы.
3)Предел функции на бесконечности.
(2.1.9)
4) Основные теоремы о пределах.
1))
(y1
± y2)
=
y1
±
y2
(2.1.10)
2))
(y1
y2)
=
y1
y2
(2.1.11)
Постоянный множитель можно выносить за знак предела.
3))
(2.1.12)
4))
Если между соответствующими значениями
функций u
= u
(x),
v=
v
(x),
w
= w(x)
при x→x0
выполняются неравенства u
≤ v
≤ w
и при этом
u
= A
и
w
= A,
то и
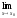v
= A.
(2.9.13)
5))
Если при x→x0
y
(x)
≥ 0,
то и
y(х)
= A
≥ 0
(2.1.14)
6))
Если U1
(x)
≥ U2
при x→x0,
то и
U1(x)
≥
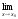U2(x)
(2.1.15)
Типовые примеры.
1.
Доказать, что
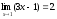
Решение.
Пусть
у=3х-1,
>0.
Для данного
>0
требуется найти такое
>0,
что для
<
<
.
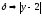Последнее неравенство имеет вид: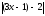
<
<
<
,
из чего следует, что для всех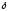
<
<
,
то есть
Замечание.
Если
при вычислении предела нет особенностей,
например, неопределённостей, то предел
вычисляется методом предельного
перехода, то есть прямой подстановкой
предельного значения переменной величины
х
в предел. Например:
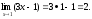
Лекция 10.
Тема 2.2. Предел и непрерывность функции.
2.2.1.Первый
и второй замечательные пределы. Раскрытие
неопределённостей типа
.
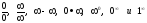2.2.2.Непрерывность функции.
2.2.3.Бесконечно малые и бесконечно большие функции.
2.2.1. Первый и второй замечательные приделы. Раскрытие неопределённостей типа .
Первый замечательный предел.
(2.2.1.)
2) Второй замечательный придел.
(2.2.2.)
(2.2.3.)
Число Непера: е = 2,71828.
3) Натуральные логарифмы
logе.x = ln x (2.2.4.)
lg N 0,43429 ln N
4)
Раскрытие неопределённостей типа
.
Типовые примеры.
1.
Решение.
2.
Решение.
.
3.
4. lg e 0,43429 ln e 0,43429.
5.
Решение.
6.
Решение.
7.
Решение.
.
8.
Решение.
9.
Решение.
10.
Решение.
.
11.
Решение.
.
2.2.2. Непрерывность функции.
1) Основные понятия.
Функция
y
= y(х)
непрерывна в точке х0,
если
,
где
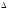х
= х – х0,
у
= у – у0,
у0
= у (х0).
2) Основные теоремы о непрерывных функциях.
1)) Если функция f(x) непрерывна на [a,b] и на концах отрезка принимает значения разных знаков, то найдется такая точка С(аСb), что f(C) = 0.
2)) Если функция у = у(х) определена и непрерывна на [a,b] и f(a) = A, f(b) = B и АСВ, тогда найдется такая точка сε(а,b), что f(c) = C.
3) Точка разрыва функции.
Различают два типа точек разрыва.
Если
для функции у
= у(х)
существуют конечные пределы
,
,
причем не все три числа
,
и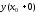
равны между собой, то точках0
называется точкой разрыва 1-го рода.
Точки разрыва 1-го рода, у которых
,
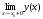называется устранимой точкой разрыва
1-го рода
Точки разрыва функции, не являющиеся точками разрыва 1-го рода, называются точками разрыва 2-го рода.
Типовой пример.
Доказать, что функция у = х2 непрерывна.
Доказательство:
.
означает, что функцияу
= х2
в точке х
непрерывна.
2.
Исследовать на непрерывность функцию
.
Ответ: точка х=2 является точкой разрыва, так как в ней функция у=у(х) не определена.