128Regular intergrowth of crystals

(1)epitaxy;

(2)syntaxy or topotaxy;

(3)exsolution or precipitation;

(4)spinodal decomposition.

7.2Twinning

7.2.1Types of twinning

Twinning is an intergrowth relation between two individuals of the same crystal species by a symmetry operation which is not included in the single crystal, formed through the processes of growth, transformation, and deformation. They are referred to as growth twinning, transformation twinning, and deformation, mechanical or secondary twinning, respectively.

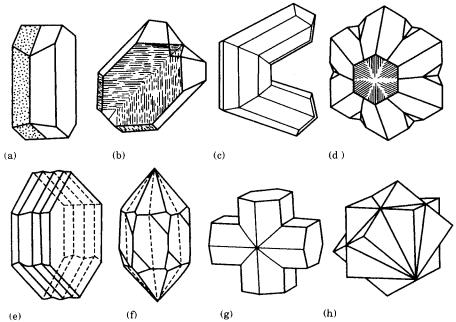
Two different concepts have been introduced as symmetry elements that introduce the twin relation: one allows a center of symmetry, a symmetry plane, and two-fold rotation axis only; the other allows a rotation axis higher than three-fold [1]. In this book, we follow the first concept, and consider twinning by higher than three-fold rotation as a repeated symmetry operation of a two-fold axis. Symmetry elements that produce twin relations are referred to as the center of twin, the twin plane, and the twin axis. During a twinning operation, a composition plane and a re-entrant corner are introduced between the two individual crystals. A twinning relation in which the twin plane and the composition plane are the same is called a contact twin, and the composition plane is, in general, a low-index crystal face. There are also twinning relations in which two individuals are mutually penetrated, and in this case the composition plane of the two individuals is an irregular boundary plane. These are called penetration twins. When a twinning relation is repeated, a lamellar twin, an elbow twin, or a cyclic twin is formed. Examples are shown in Fig. 7.1.

7.2.2Energetic considerations

A twin, in which a composition plane is newly introduced between two individuals, is in a state such that the energy corresponding to the interface is newly added to the energy state of the single crystal, which is in the minimum energy state. To form a twin, a driving force is required to overcome this additional energy, which automatically leads to a prediction that the smaller the interface energy, the higher the probability that twinning will occur.

The interface energy comes from a mismatch of atomic positions on the interface. If there is good coherency in atomic positions and bonds between the two individual crystals, the additional energy is small, and the probability of forming a twin is high. In the situation with less coherency or continuity and larger mis-

7.2 Twinning 129

Figure 7.1. Various growth twins. (a) Contact twin (albite); (b) inclined twin (quartz);

(c) elbow twin (rutile); (d) cyclic twin (chrysoberyl); (e) lamellar twin (albite);

(f) penetration twin (quartz); (g) penetration twin (staurolite); (h) penetration twin (fluorite).

match on the interface, the interface energy is large, and the probability of intergrowing in a twin relation is low.

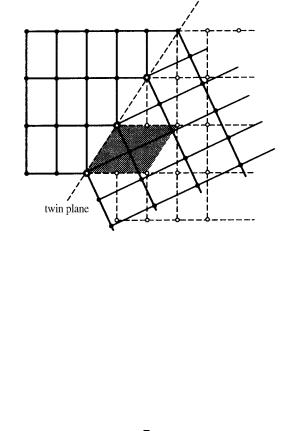
Before interface energy was understood, the concept was explained by Friedel [2] in terms of a compound or twin lattice. This may be explained as follows (see Fig. 7.2). If the lattice of one individual crystal is extended to superpose that of the other, where both are projected onto the same plane, a new lattice consisting of common lattice points results. This lattice is called a twin lattice or compound lattice, and the twin index is defined by the number of multiples of the unit cell size of a single crystal. The smaller the twin index, the higher the probability that twinning will occur.

The concept of the coincidence site lattice (CSL) due to Kronberg and Wilson [3] is an extension of Friedel’s twin lattice. If two lattices are superimposed and one is rotated about an axis, a series of compound lattices consisting of coincident sites appear as the rotation angle changes. The compound lattices appearing in this way are larger than the basic lattice, and their sizes change according to rotation angle. Kronberg and Wilson explained that the rotation angle producing the smaller CSL is the one that leads to a higher probability of intergrowth. This is

130 Regular intergrowth of crystals

Figure 7.2. Friedel’s concept of a compound or twin lattice. Assuming that atomic

positions are adjusted elastically at lattice points, the twin index of the twin lattice is 2.

related to the value of interface free energy at the composition plane and the probability of producing a crystallographic intergrowth relation. Both twinning and CSL involve probability, and the probability increases if the size of the common lattices is smaller. It should be understood that the term “twin” is applied to the interactions occurring at higher probability than other intergrowth relations.

Aragonite is a high-pressure polymorph and calcite is a high-temperature polymorph of CaCO3. Aragonite belongs to the orthorhombic system mmm, and calcite

is part of the trigonal system, 3m. Aragonite occurs, in most cases, as a cyclic twin showing a pseudo-hexagonal form by repeated twinning on {110} as the composition and twin plane, whereas calcite occurs less frequently as a twin. The reason for this discrepancy has been accounted for in terms of the twin lattice or the difference in how many unit cells there are in a CSL.

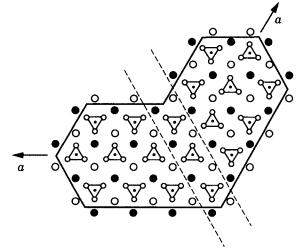
Both Friedel’s twin lattice and Kronberg and Wilson’s CSL are related at unit cell level; both explain well, at least qualitatively, the twin relations, including the probability. At the structural level within the crystal, this corresponds to a problem in continuing the structure of two individual crystals across the composition plane; put another way, we have a problem of whether there is a good coherency or not. Figure 7.3 is taken from Bragg and Claringbull [4], which explains the twin of aragonite. There is not an unreasonably large distortion in the positions and continuation of ions of Ca and CO3 across the boundary plane.

In close-packed structures, a twin relation is introduced by a stacking fault. In this case, there are no obstacles to the continuation of the structure, other than the stacking fault itself. However, in some twinning relations, strain due to mis-

7.2 Twinning 131

Figure 7.3. Structure of aragonite twin [4]. Triangles denote CO3, and the solid and open circles represent Ca.

match is released by the introduction of dislocations. The Brazil twin of quartz is such an example, in which a dislocation is always present at the termination of the twin lamellae (see Chapter 10).

To form a twin that is in a higher energy state than a single crystal, by an amount equal to the interface energy, we require a higher driving force, which will overcome this excess energy. If nucleation takes place under a higher driving force condition than that required for the nucleation of a single crystal, the probability of formation of a twinned nucleus increases. From an energy standpoint, the prediction is that the probability of formation of a growth twin will be highest in the nucleation stage under a high driving force condition, i.e. at high-supersaturation condition, and the probability will diminish sharply in the growth stage when the driving force is lowered. This analysis was made by Buerger [5]. Two individual single crystals joined in a twin relation during the nucleation stage (i.e. a growth twin) should therefore develop to become equal in size; observations confirm this prediction. A high driving force not only results from a high-supersaturation condition, but also for other reasons, such as the presence of appropriate impurity components, or mechanical shock in the nucleation stage.

Although the probability of twin formation occurring during growth is far lower than that during nucleation, there is a possibility that growth twins, formed by the conjoining of two individuals during growth, will result. In this case, it is necessary that the two individual crystals have polyhedral forms bounded by flat faces. This flat face acts as the composition plane, which is equal to the twin plane. The

132 Regular intergrowth of crystals

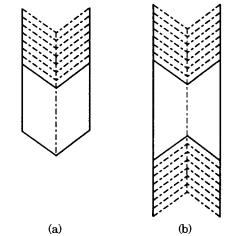
Figure 7.4. The re-entrant corner effect. (a) One re-entrant corner; (b) two re-entrant

corners, one at each end.

sizes of the two individual crystals may be different. The probability of joining an individual in a twinning relation along the edges or at the corners of another larger crystal is much lower than the probability of twinning on a flat face.

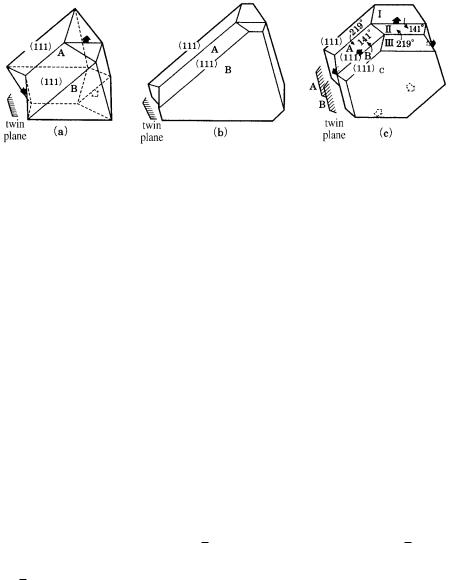
7.2.3Re-entrant corner effect and pseudo re-entrant corner effect

A re-entrant corner (edge, see Fig. 7.5(c)) is introduced between two individuals by twinning. Due to the presence of a re-entrant edge (corner), a re-entrant corner is an energetically more favorable site for two-dimensional nucleation than is a flat face. This results in a different morphology for a twinned crystal than for a single crystal. In twin relations with only one or two re-entrant corners (Fig. 7.4), the twinned crystal takes an elongated or ribbon form along this direction, and in twin relations with three re-entrant corners (Fig. 7.5), the twin takes a triangular form, as opposed to the octahedral form of the single crystal. If several twin planes are introduced repeatedly in this twin, re-entrant corners appear in six directions, and thus preferential growth sites do not disappear for ever, resulting in the formation of a ribbon crystal as long as nutrient is supplied. (This principle is used in the synthesis of Ge ribbon crystals [6].) The re-entrant corner effect [7] was proposed to account for the origin of a characteristic morphology of twinned crystals that is different from that of single crystals in terms of preferential growth at the reentrant corners.

As another example of utilizing platy forms of twinned crystals, we should mention a recent remarkable increase in the photosensitivity of photographic film. Photographic emulsion film consists of minute AgBr crystallites, with octahedral or cubo-octahedral Habitus. The photosensitivity is determined by the area

7.2 Twinning 133

Figure 7.5. (a) Twin with re-entrant corners in three directions (shown by arrows) and

(b) its expected re-entrant corner effect. (c) Morphological change is expected for repeated twinning.

covered by these crystals. However, if the probability of twinning is increased by controlling the conditions, the area covered by the crystals increases greatly, since twinned crystals take triangular or hexagonal platy Habitus, so increasing the photosensitivity.

Real crystals contain dislocations, which act as self-perpetuating growth sites. In some twin relations, dislocations are present in the twin plane or concentrate in the composition plane as growth proceeds. Since growth mediated by dislocations is energetically more advantageous than that mediated by re-entrant corners, either a unidirectional elongated form appears, or the twin grows in a similar form in real crystals, as shown schematically in Fig. 7.6, because both re-entrant and protruded sides grow similarly. This means that, in real crystals, the re-entrant corner effect, in its original meaning, cannot be expected to operate. However, many actual twins have sizes and morphologies different from those of coexisting single crystals. A good example may be seen in quartz twinned crystals, which adhere to the Japan law, which grow larger and show a more flattened characteristic V-shape or fan-shape than do hexagonal prismatic forms of coexisting single crystals, which will be discussed in detail in Chapter 10. This is because dislocations converge in the composition plane {1122} and promote the growth of {1011} faces adjacent to the composition plane above that on crystallographically equivalent {1011} faces on the opposite, non re-entrant corner, side. On the opposite protruding side, with no re-entrant corner, dislocations diverge as growth proceeds from the composition plane, and so preferential growth at the twin junction does not occur. Since this type of re-entrant corner effect is due to preferential growth caused by re-entrant concentration of dislocations, the effect is called the pseudo or apparent re-entrant corner effect [8].

In close-packed structures or fcc crystals, twinning is introduced by stacking faults. In this case, the excess energy at the twin plane ( composition plane) is small, and so neither generation nor concentration of dislocations is required. In