4

Factors determining the morphology of polyhedral crystals

Polyhedral crystals bounded by flat faces can exhibit various Tracht and

Habitus because they result from the interconnection of internal structural factors and the external factors involved during crystal growth. The concepts of the structural form and the equilibrium form were first suggested in an attempt to provide a greater understanding of the origin of the morphology of polyhedral crystals. Furthermore, extensive experiments on and observations of natural minerals were carried out in an attempt to clarify the origin of morphological variation of growth forms. The results obtained from the many investigations performed in the twentieth century are summarized in this chapter.

4.1Forms of polyhedral crystals

The various morphologies, such as polyhedral, hopper, dendritic, and spherulitic, that are exhibited by single crystals and polycrystalline aggregates, have been discussed in relation to the driving force in the preceding chapters.

Among all of the various morphologies exhibited by crystals, it is the problem of variations in Tracht and Habitus exhibited by polyhedral single crystals that has attracted the deepest concern. Polyhedral single crystals are expected when crystals grow by the spiral growth mechanism under a driving force of /kT *. There are four logical routes that we can take to understand this problem.

The first is the prediction of the Habitus made from the characteristics of the crystal structure, entirely neglecting the effect of growth conditions. We will call this the “structural form” or “abstract form.” The second logical approach is to predict the Habitus thermodynamically when the crystal reaches the equilibrium state. This may be called the “equilibrium form.” The third is a method of analyzing the factors that may have an effect by correlating the Habitus and Tracht shown

4.2 Structural form 61

by real crystals and their growth conditions. Investigations of this type may be referred to as “growth forms.” It should be noted that, whereas structural and equilibrium forms may be described as singular, growth forms are plural. The fourth method is to analyze the growth forms based on the observation of surface microtopographs of crystal faces, possible now that molecular information relating to growth forms is available.

We discuss the structural form in Section 4.2 and the equilibrium form in Section 4.3. Section 4.4 presents a summary of the results and investigations of the growth forms. The subject of microtopographs will be discussed in Chapter 5.

4.2Structural form

The morphology of real crystals is determined by two factors: the internal elements, due to the periodicity and anisotropy of the bonding that constitutes the crystal structure, and the external elements involved in the growth parameters. If a crystal grows in an isotropic ambient phase, crystal species having different structures will show characteristic Habitus corresponding to the respective structures. However, the same crystal species may show various Habitus, including dendritic form, depending on the growth conditions. It is known empirically that the order of morphological importance of crystal faces, deduced from statistical treatments of the development and frequency of appearance of faces on polyhedral crystals of a particular crystal species, is closely related in many cases to the lattice type of the crystal.

In Fig. 4.1 we depict three lattice types of the cubic system and the crystal faces with the highest reticular density (the density of lattice points per unit area) in each type.

The crystal face with the highest reticular density (and thus with the widest reticular spacing) is {100} in the simple cubic lattice (P), {111} in the face-centered cubic lattice (F), and {110} in the body-centered cubic lattice (I). The order of morphological importance obtained statistically from mineral crystals agrees well with this in many cases. This is known as the Bravais empirical law [1], the earliest law presented to describe the morphology of polyhedral crystals. There are, however, cases in which there is no agreement. For example, the polyhedral form of quartz predicted from the consideration of its lattice type should be bounded by three equally developed faces, {0001} {1010} {1011} (Fig. 4.2(a)); however, the {0001} face appears only exceptionally rarely in real quartz crystals. In pyrite crystals, {110} should develop as a large face, but in reality pyrite is mainly bounded by {210}, and the order of morphological importance of {110} is very low.

Lattice type is the basis of calculation of reticular density in the Bravais empirical law. In lattice types, only the symmetry elements with no translation, i.e. the

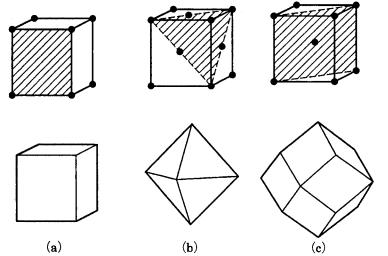
62 Morphology of polyhedral crystals

Figure 4.1. Crystal faces with the highest rank in the order of morphological importance (with the highest reticular density) for P, F, and I lattice types of the cubic system: (a) P lattice, {100}; (b) F lattice, {111}; (c) I lattice, {110}.

center of symmetry, the symmetry plane, and the symmetry axes, are included. This means that the geometry of the fourteen types of Bravais lattice and thirtytwo crystal groups form the basis of the analysis. In the structural analysis, the 230 space groups containing translational symmetry elements, i.e. glide planes and screw axes, are required. In quartz crystal containing a three-fold screw axis, the reticular density of {0001} should be calculated as {0003} (see Fig. 4.2 (b)), and in pyrite {110} should be treated as {220} (due to the presence of a glide plane), and so the reticular density becomes half that calculated on {110}. If the reticular densities of crystal faces are recalculated by expanding the symmetry elements involved in the thirty-two point groups to those in the 230 space groups, most of the discrepancies between the predicted forms determined from the Bravais empirical law and those that are actually observed disappear. This is an extension of the Bravais (and Friedel) empirical law by Donnay and Harker [2], which we shall abbreviate as the BFDH (Bravais–(Friedel)–Donnay–Harker) law. We see that, in the BFDH law, crystal forms are analyzed by considering the crystal faces.

Polyhedral crystal forms are defined by faces (planes) and edges (zones). One treatment that focuses mainly on the zones is the periodic bond chain (PBC) theory by Hartman and Perdok [3], and see ref. [12], Chapter 3. If we connect atoms and ions having strong bonding in a crystal structure, we find a few strongly bound chains in the structure. Since these chains are arranged periodically, they are called periodic bond chains (PBCs), which are vector quantities. We may define a PBC by its stoichiometric composition. PBCs containing only an integer fraction of composition

4.2 Structural form 63

Figure 4.2. The morphology of quartz crystal predicted by (a) the Bravais empirical law

and (b) Donnay–Harker’s law.

are partial PBCs, but these are not considered in HP (Hartman–Perdok) theory. Crystal faces are classified into three types, depending on the number of PBCs included:

(i)K face (kinked face), containing no PBCs;

(ii)S face (stepped face), containing only one PBC;

(iii)F face (flat face), containing two or more PBCs.

It is clear that K, S, and F faces correspond to the (111), (110), and (001) faces, respectively, of the Kossel crystal shown in Fig. 3.9 (Fig. 4.3). A K face corresponds to a rough interface, an F face to a smooth interface, and an S face to a face having an intermediate nature between that of the K and F faces. Further, a K face grows by the adhesive-type growth mechanism, an F face grows either by a layer-by-layer or a spiral growth mechanism, and an S face appears by the piling up of growth layers advancing on the neighboring F face. Therefore, an F face develops to a large size in order to control Habitus and Tracht in a real crystal, the K face will disappear from the crystal surface, and the S face will be characterized by striations only, if it appears on a crystal.

Another advantage of the PBC theory is its ability to predict not only the bulk morphology of a polyhedral crystal, but also the morphology of growth layers developing on F faces. When growth layers are polygonal, the step direction is assumed to be defined by the PBC theory. These predictions cannot be made by the BFDH law.