2.2. Проекции прямых линий

Положение прямой линии в пространстве вполне определяется двумя ее любыми точками. В общем случае проекцией прямой является прямая, в частном случае - точка, если прямая перпендикулярна плоскости проекций. Для построения проекций прямой достаточно иметь либо проекции двух ее точек, либо проекцию одной точки прямой и направление прямой в пространстве.

По своему расположению в пространстве относительно плоскостей проекций прямые линии разделяют на прямые общего положения, уровня и проецирующие.

2.2.1. Прямые общего положения. Это прямые, не параллельные и не перпендикулярные к плоскостям проекций. ПроекцииА₁В₁, А₂В₂иА₃В₃отрезкаАВпрямойАВобщего положения (рис. 2.18,а) наклонены под острыми углами к осямx₁₂, y₁₃иz₂₃. Длины проекций отрезков этой прямой всегда меньше самого отрезка. Трехкартинный комплексный чертеж отрезка прямой общего положения, построенный по двум точкамАи В, показан на рис.2.18, б.

2.2.2.Прямые уровня.Это прямые, параллельные одной из плоскостей проекций -П₁, П₂илиП₃. Следовательно, имеем три вида прямых уровня:

1) горизонтальная уровняa(горизонталь), параллельнаяП₁(прямаяa с отрезкомAB на ней на рис. 2.19,а,б);

2) фронтальная уровня(фронталь), параллельнаяП₂(прямаяbcотрезкомCDна ней на рис. 2.20,а);

3) профильная уровня, параллельнаяП₃(прямаясс отрезкомЕFна ней на рис. 2.20,б). На рис. 2.20 наглядные изображения прямыхb иcотносительно плоскостей проекций не показаны.

О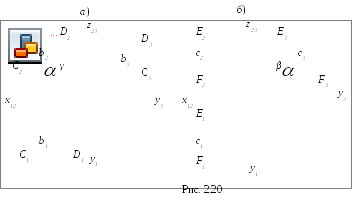дноименные проекции отрезков прямых уровня проецируются в натуральную величину, а разноименные параллельны осям, отделяющим их от одноименных. При этом для горизонтали одноименная проекция - горизонтальная, а разноименные - фронтальная и профильная и т. п.

Углы наклона прямых уровня a, bиcк плоскостям проекцийП₁,П₂иП₃ принято обозначать соответственноα,βи γ(на рис. 2.19 углыα,βи γне показаны).

2.2.3. Проецирующие прямые. Это прямые, перпендикулярные к одной из плоскостей проекций и параллельные двум другим. Следовательно, имеем три вида проецирующих прямых:

1) горизонтально-проецирующаяпрямая, перпендикулярная П₁(прямаяас отрезкомABна ней на рис. 2.21,а);

2) фронтально-проецирующаяпрямая, перпендикулярная П₂(прямаяb с отрезкомCDна ней на рис. 2.21,б);

3) профильно-проецирующаяпрямая, перпендикулярная П₃(прямаяcс отрезкомEFна ней на рис. 2.21,в).

На рис. 2.21 в скобки заключены проекции невидимых точек. Вопрос определения видимости точек на проекциях подробнее будет рассмотрен ниже в п. «Скрещивающиеся прямые».

У проецирующих прямых одноименные проекции представляют собой точки, что вытекает из существа проецирующей прямой, вдоль которой ведется проецирование.

Каждая разноименная проекция проецирующей прямой перпендикулярна оси, отделяющей ее от одноименной проекции, а разноимённая проекция отрезка, расположенного на прямой уровня, является натуральной величиной этого отрезка.

2.2.4. Определение натуральной величины отрезка прямой общего положения. Натуральную величину прямой частного положения можно сразу определить на комплексном чертеже этой прямой.

Для определения натуральной величины отрезка прямой общего положения можно применить рассмотренный ранее (см. п. 2.1.2)способ замены плоскостей проекций. На рис.2.22 показано определение натуральной величины (Н.В.) отрезкаAB прямой общего положения и определение углов наклона его кΠ₁( уголα) и кΠ₂ ( уголβ) этим способом.

Дополнительная плоскость Π₄ проведена параллельно AB(х₁₄||A₁B₁).ПрямаяABпреобразована в положение фронтали, следовательноA₄B₄ – натуральная величинаAB.

Проведя дополнительную плоскость Π₅||AB (х₂₅||A₂B₂), также можно определить натуральную величину AB.A₅B₅ – натуральная величина AB. ПрямаяABв системеΠ₂-Π₅стала горизонталью.

На рис.2.23 показано определение натуральной величиныAB методом треугольника. Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – алгебраическая разность расстояний его концов от плоскостиΠ₁ (ΔZ).

2.2.5. Взаимное положение прямых. Прямые линии в пространстве могут быть параллельными, пересекаться и скрещиваться.

Параллельные прямые.Из свойств параллельных проекций следует, что если прямые в пространстве параллельны, то все три пары их одноименных проекций параллельны. Очевидно и обратное положение:если одноименные проекции прямых параллельны, то прямые в пространстве параллельны.

Для определения параллельности прямых в общем случае достаточно параллельности двух пар одноименных проекций. В случае, если определяется параллельность линий уровня, то одной из двух пар параллельных проекций должна быть проекция на одноименную плоскость.

Н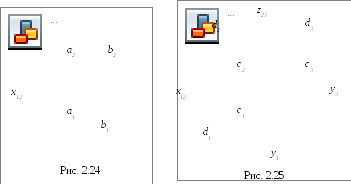а рис. 2.24 показаны проекции параллельных прямыхaиbобщего положения, гдеa₁║ b₁иa₂║ b₂. На рис. 2.25 показаны две горизонталиcиd. У горизонталей фронтальные и профильные проекции всегда параллельны осям, отделяющих их от одноименных горизонтальных проекций, т. е.c₂║ d₂║ x₁₂ и c₃║ d₃║ y₃. Но горизонтальные их проекции не параллельны, т. е.c₁╫ d₁. Следовательно, прямыеc иd не параллельны.

Пересекающиеся прямые.Две пересекающиеся прямые лежат в одной плоскости и имеют одну общую точку. Из свойств параллельных проекций известно, что если точка лежит на прямой, то ее проекции лежат на проекциях прямой. Если точка лежит и на той и на другой прямой, т. е. в точке пересечения прямых, то ее проекция должна лежать сразу на двух одноименных проекциях прямых, а следовательно, в точке пересечения проекций прямых.

Так, если отрезки ABиCDдвух прямых пересекаются в точкеK, то проекции отрезковA₁B₁иC₁D₁пересекаются в точкеK₁, являющейся проекцией точкиK(рис. 2.26, а). Поэтому,если одноименные проекции прямых пересекаются в точках, лежащих на одной линии проекционной связи, то прямые в пространстве пересекаются (рис. 2.26,б).

Для определения того, пересекаются прямые или нет, достаточно, чтобы это условие выполнялось для двух каких-либо проекций. Исключение составляет случай, когда одна из пересекающихся прямых является профильной уровня. В этом случае для проверки пересечения прямых необходимо построение профильной проекции.

Пусть через точку Aнеобходимо провести горизонтальb, пересекающую прямуюa(рис. 2.27,а). Для этого через точкуA₂ проводимb₂║ x₁₂(этап 1) до пересечения сa₂в точке K₂(рис.2.27,б). Далее с помощью линии проекционной связи наa₁находим точкуK₁ (этап 2) и, соединяя точкиA₁ иK₁ (этап 3), получаем b₁.

Скрещивающиеся прямые. Скрещивающиеся прямые aиbне лежат в одной плоскости и, следовательно, не параллельны и не имеют общих точек (рис.2.28,а). Поэтому, если прямые скрещивающиеся, то хотя бы одна пара их одноименных проекций не параллельна, и точки пересечения одноименных проекций не лежат на одной линии проекционной связи (рис. 2.28,б).

Каждая такая точка пересечения является проекцией двух точек, принадлежащих прямым; эти две точки лежат на одном проецирующем луче и называются конкурирующими.

K₁≡(L₁)

Точки KиL(рис. 2.28,а) лежат на одном горизонтально-проецирующем луче. Горизонтальные проекции точек совпадают и находятся в точке пересечения горизонтальных проекцийa₁иb₁прямых. ТочкаK a, точкаL b. Видно, что точкаKвыше точкиL. Считают, что при проецировании наП₁точкаKвидна, а точкаL- не видна (закрыта от наблюдателя точкойК).

Точки Mи Nлежат на одном фронтально-проецирующем луче (рис. 2.28,б). Фронтальные проекции точек совпадают и находятся в точке пересечения фронтальных проекций прямыхa₂иb₂. ТочкаM a, точкаN b. ТочкаNдальше отП₂, чем точкаM, т. е. ближе к глазам наблюдателя, и поэтому при проецировании наП₂ точка Nвидна, а точкаM- не видна. Обозначения проекций невидимых точек принято заключать в круглые скобки.