3.2. Пересечение геометрических объектов, когда один из геометрических объектов проецирующий, а другой непроецирующий

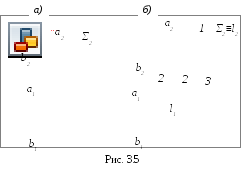
3.2.1. Построение линии пересечения двух плоскостей. На рис. 3.5,азаданыΤ (а∩b) – плоскость общего положения, иΣ– фронтально-проецирующая плоскость. Фронтальная проекция линии пересечения плоскостейℓ (ℓ₂) совпадает со следом плоскостиΣ(Σ₂), т. е.Σ₂≡ℓ₂. Горизонтальную проекцию линииℓ (ℓ₁) находим по принадлежности линииℓплоскостиΤ (рис. 3.5,б)

3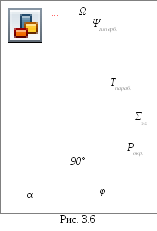.2.2. Линии пересечения конической поверхности с плоскостями.Прямой круговой конус имеет пять видов линий пересечения в зависимости от положения секущей плоскости по отношению к оси конуса.

Обозначим угол между образующей конуса и его осью буквой φ, а угол между секущей плоскостью и осью конуса буквойα(рис. 3.6).

Возможны следующие виды линий пересечения:

1) если α=90°, то плоскостьPпересекает поверхностьпо окружности;

2) если 90°>α>φ, то плоскостьΣпересекает поверхностьпо эллипсу;

3) если α=φ, т. е. секущая плоскостьΤпараллельна одной образующей, то поверхность пересекаетсяпо параболе;

4) если 0≤α<φ, т. е. секущая плоскостьΨпараллельна двум образующим, то поверхность пересекаетсяпо гиперболе;

5) если 0≤ α<φи секущая плоскостьΩпроходит через вершину конуса, то поверхность пересекаетсяпо двум образующим.

3.2.3.Построение проекций и натуральной величины линии пересечения конической поверхности с плоскостью. На рис. 3.7 заданы коническая поверхность и фронтально-проецирую-щая плоскостьТ. В данном случае при пересечении получаетсяпарабола. Так как плоскостьΤ_┴ Π₂ , то фронтальная проекция параболы совпадает сΤ₂.

Для того, чтобы построить горизонтальную проекцию параболы, на её фронтальной проекции отмечаем ряд точек 1₂,…,7₂. Горизонтальные проекции точек1₁,…,7₁строим с помощьюпараллелей.

Натуральную величину параболы строим по точкам с помощью введения дополнительной плоскости проекций Π₅||Τ. Так как парабола является симметричной фигурой, то для удобства построений осьх₁₂взята совпадающей с осью симметрии горизонтальной проекции конуса. Осьх₂₅||Τ₂. Построение видно из чертежа.

3.2.4. Построение проекций и натуральной величины линии пересечения сферы с плоскостью. При пересечении сферы с любой плоскостью образуетсяокружность.

На рис. 3.8 сфера пересекается горизонтально-проецирующей плоскостью Σ. Окружность, получаемая при пересечении плоскостиΣсо сферой, при проецировании наΠ₁ совпадает соследом плоскости Σ (Σ₁)– это отрезок1₁-2₁. На фронтальную плоскость Π₂ окружность проецируется в видеэллипса,причём1₂-2₂– малая ось эллипса,3₂-4₂– большая ось эллипса. Промежуточные точки можно построить с помощью параллелей.

Натуральная величина окружности построена с помощью введения дополнительной плоскости проекций Π₄||Σ. Осьх₁₄ проводим параллельноΣ₁.

Построение видно из чертежа.

3.2.5. Построение проекций линии пересечения конуса и призмы. На рис. 3.9 заданы конус и призма. В данном случае три грани призмы перпендикулярныΠ₂, поэтому фронтальная проекция линии пересечения совпадает с фронтальной проекцией призмы1₂-3₂-5₂.

Горизонтальная проекция линии пересечения построена по принадлежности конусу с помощью параллелей.

Таким образом, когда один из пересекающихся геометрических объектов проецирующий, а другой непроецирующий, то одна из проекций линии пересечения на чертеже уже определена, а другая проекция определяется по принадлежности непроецирующему геометрическому объекту.