3.4. Пересечение линии с поверхностью

3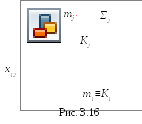.4.1. Пересечение линии с поверхностью, когда оба геометрических объекта проецирующие.На рис. 3.16 показано пересечение фронтально-проецирующей плоскостиΣи горизонтально-проецирующей прямойm.

Так как плоскость Σи прямаяm проецирующие, то проекции точки их пересечения (точкаK) на чертеже уже определены, их надо только отметить (K₂иK₁).

3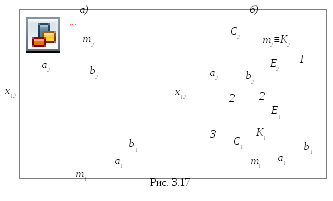.4.2. Пересечение линии с поверхностью, когда один из пересекающихся геометрических объектов проецирующий, а другой – непроецирующий.На рис. 3.17 показано определение точки пересечения плоскостиΣ (a||b) и прямойm. Σ∩m=K.

Так как прямая m_┴Π₂ (рис. 3.17,а), тоK₂≡m₂ (рис. 3.17,б), аK₁находим из условия принадлежности точкиKплоскостиΣс помощью вспомогательной прямойCEΣ. Ход построения указан на чертеже.

На рис. 3.18 показано построение точек пересечения прямых dиm с конической поверхностьюΦ.d∩Φ=K, m∩Φ=C и B.

Так как d_┴Π₁, тоK₁≡d₁, аK₂ находим с помощью образующейS.

П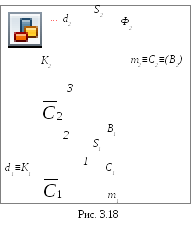рямаяm_┴Π₂, поэтому фронтальные проекцииC₂и B₂ точек пересечения прямойmс конусом совпадают сm₂, аC₁иB₁находим с помощью параллели.

3.4.3. Пересечение линии с поверхностью, когда оба геометрических объекта непроецирующие. Для определения точек пересечения линии с поверхностью (рис. 3.19) необходимо:

1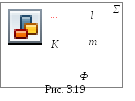) заключить линию (m) во вспомогательную поверхность:Σm.Желательно, чтобы при пересеченииΣс заданной поверхностьюΦполучались прямые или окружности;

2) определяем линию пересечения ℓвспомогательной поверхностиΣиΦ.Σ∩Φ=ℓ;

3) определяем точки пересечения построенной линии ℓ сm, то естьℓ∩m=K^ί;

4) определяем видимость заданной линии.

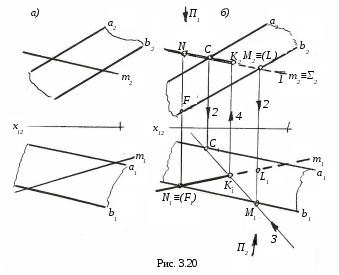
На рис. 3.20 показано построение точки пересечения прямой общего положения mс плоскостьюΦ (a||b) (рис. 3.20, а) и m∩Φ=K (рис. 3.20, б).

Ход построения:

1) заключаем прямую mво фронтально-проецирующую плоскостьΣ (Σm), то есть черезm₂проводимΣ₂;

2) строим линию пересечения плоскостей Σ иΦ. Это прямаяCM (C₁M₁, C₂M₂). CM=Σ∩Φ;

3) определяем точку K пересеченияmсCM. Сначала определяем точкуK₁ (K₁= m₁∩C₁M₁), а затем с помощью линии проекционной связи - точкуK₂ (K₂m₂);

4) видимость прямой mи плоскостиΦопределяем с помощью конкурирующих точек: наΠ₁– с помощьюNиF; наΠ₂– с помощьюLиM.

На рис. 3.21 показано построение точек пересечения горизонтали hсо сферойΦ.

Ход построения:

1) заключаем прямую hв горизонтальную плоскостьΣh(Σ₂≡h₂);

2) строим линию пересечения ℓ(окружность радиусаR) плоскостиΣсо сферой.Σ ∩Φ=ℓ;

3) определяем точки пересечения линии ℓс горизонтальюh.ℓ∩h=KиM. Сначала отмечаем точкиK₁иM₁, а затем с помощью линий проекционной связи находимK₂иM₂на h₂;

4) определяем видимость линии m.

Построение точек пересечения прямой общего положения mсо сферой Φприведено на рис 3.22.

Для определения искомых точек пересечения выполним следующие построения:

1) заключаем прямую mв горизонтально-проецирующую плоскостьΣ (Σ₁m₁).

При пересечении Σсо сферой получается окружность, которая наΠ₂ спроецируется в виде эллипса. Чтобы избежать построения эллипса, с помощью метода замены плоскостей проекций преобразуем прямуюmв положение линии уровня, тогда дальнейшее построение будет подобно примеру на рис. 3.21.

Для этого:

2) на прямой m задаём две точки AиB;

3) проводим дополнительную плоскость Π₄||m (х₁₄||m₁);

4) Проецируем на Π₄прямуюABи сферу. В новой системеΠ₁-Π₄прямая m стала фронталью (m₁, m₄);

5) Σ∩Φ=ℓ(окружность радиусаR);

6) ℓ ∩ m=KиM, то естьℓ₄ ∩ m₄=K₄иM₄.K₁иM₁,K₂иM₂ находим по линиям проекционной связи;

7) Определяем видимость mнаΠ₁иΠ₂.

Н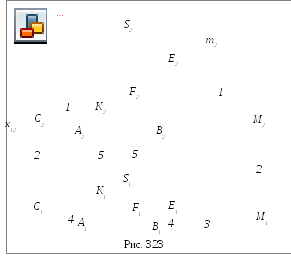а рис. 3.23 показано построение точек пересечения прямой общего положенияmс конусом.

В данном случае удобнее всего, чтобы вспомогательная плоскость Σпересекала конус по двум образующим, то есть вспомогательная плоскость должна проходить через вершину конусаS. Эта плоскость уже задана на чертеже прямойmи точкойS, то естьΣ (S, m).

Для удобства построений переходим к заданию плоскости Σ пересекающимися прямыми. Для этого на прямойmзадаём точкуE (E₁, E₂) и соединяем её с вершинойS. Теперь плоскостьΣ задана двумя пересекающимися прямыми:Σ (m∩SE).

Далее строим линию пересечения ΣсΠ₁, это линияCM. Для этого находим горизонтальные следы прямыхm и SE, этоC₁иM₁.

Горизонтальный след Σ (CM) и основание конуса лежат в одной плоскости, поэтому линияCMпересекает основание конуса в точкахAиB, которые соединяем с вершинойSи получаем образующиеAS иSB, по которым Σ пересекает конус.

Затем строим точки пересечения AS иSBс прямойm.AS∩m=K,BS∩m=F.

Таким образом точки KиF- искомые точки. Далее определяем видимость прямойm.