3.3. Пересечение геометрических объектов, когда оба геометрических объекта – непроецирующие

При взаимном пересечении поверхностей образуется общее множество точек, представляющих собой пространственную кривую линию. В частных случаях кривая распадается на несколько частей, каждая из которых может быть и плоской. Линию взаимного пересечения ещё называют линией перехода.

Пусть заданы две поверхности ΦиΤ (рис. 3.10). Требуется построить линию их пересеченияℓ = Φ ∩Τ.

Линию пересечения поверхностей строят по точкам, применяя способ вспомогательных поверхностей-посредников (плоскости, сферы и т. д.). Заданные поверхности пересекают вспомогательными поверхностями. Желательно, чтобы при пересечении вспомогательных поверхностей с заданными получались графически простые линии – прямые, окружности. Для упрощения построения в качестве поверхностей-посредников – применяют проецирующие поверхности.

3.3.1. Алгоритм построения линии пересечения двух поверхностей. Предварительно выполняем следующие действия:

1) Определяем, какие поверхности пересекаются.

2) Определяем характерные точки, принадлежащие линии пересечения (наивысшая и наинизшая, самая правая и самая левая точки пересечения и т. п., а также точки, принадлежащие очерковым и другим характерным образующим поверхностей).

3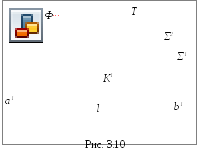) Определяем, какой способ можно применять для построения линии пересечения.

Далее переходим к собственно построению линии пересечения:

4) Для определения промежуточных точек пересекаем обе поверхности вспомогательной поверхностью Σ ¹:

а) строим линию пересечения а¹= Σ ¹∩Φ;

б) строим линию пересечения b¹= Σ ¹∩Τ¹;

в) отмечаем точки пересечения линий К¹= а¹∩ b¹.

Для построения других точек, принадлежащих линии пересечения, вводим ещё несколько вспомогательных поверхностей Σ ^ίи получаем ещё несколько точекК ^ί. Множество полученных точек будет представлять собой линию пересечения ℓдвух поверхностей;

5) определяем видимость линии пересечения и очерков поверхностей.

3.3.2. Построение линии пересечения двух плоскостей общего положения.На рис. 3.11 заданы плоскости Φ (m||n) иΤ (c∩d). Построение линии пересечения плоскостей заключается в нахождении двух точек, принадлежащих этой линии, т. к. при пересечении двух плоскостей получается прямая линия. Для определения двух точек достаточно двух плоскостей-посредников. На рис. 3.11 для нахождения одной точкиKвведена горизонтальная плоскостьΣ || Π₁.

Согласно указанному выше алгоритму:

Σ∩Φ=а, Σ∩Τ=b и а∩b=K.

Для определения второй точки K¹пересекаем плоскостиΦиΤплоскостьюΣ¹и аналогично строим вторую точкуK¹. Соединив точкиKиK¹, получаем линию пересеченияℓ = Φ ∩Τ.

3.3.3. Построение проекций линии пересечения двух кривых поверхностей с помощью вспомогательных секущих плоскостей. Сущность способа заключается в проведении семейства плоскостей, пересекающих обе поверхности по наиболее простым линиям – прямым и окружностям, либо пересекающих поверхности по кривым, проецирующимся в виде прямых и окружностей.

На рис. 3.12 показано построение проекций линии пересечения полусферы и тора.

Сначала отмечаем характерные точки: M–наивысшую,CиK– наинизшие,F иN- промежуточные.

Точка Mпринадлежит линии пересечения поверхностей, т. к. она располагается в общей фронтальной плоскости симмет-ииΤ (Τ₁), т. е. глав-ные фронтальные меридианыnиm пересекаются в точкеM, или n₂∩m₂=M₂._. M₁ находится на линии проекционной связи.

Наинизшие точки CиKнаходятся на пересечении экватора полусферы –Эи экватора тораb, т. е.Э₁∩b₁=K₁иC₁. На линии проекционной связи находим точкиK₂≡C₂.

Промежуточные точки FиNнаходим с помощью вспомогательной горизонтальной плоскостиΣ(см. вышеприведённый алгоритм), которая пересекает полусферу по окружности радиусаR₁ и тор – по окружности радиусаR₂. Эти окружности лежат в одной плоскости и пересекаются; их горизонтальные проекции пересекаются в точкахN₁иF₁, а проекцииN₂≡F₂ расположены на линии проекционной связи наΣ₂.

Проведя ещё несколько вспомогательных горизонтальных плоскостей, можно построить аналогичным путём ещё ряд промежуточных точек.

Соединив эти точки плавной кривой, получим проекции линии пересечения полусферы и тора. Затем определяем видимость линии пересечения и очерковых линий.

3.3.4. Пересечение соосных поверхностей вращения. Это поверхности, имеющие общую ось вращенияί.

На рис. 3.13 изображены соосные поверхности конуса и сферы, на рис. 3.14 – соосные цилиндр и сфера.

Соосные поверхности вращениявсегда пересекаются по окружностям,плоскости которых перпендикулярны оси вращения ί.

На рис. 3.13 и 3.14 поверхности пересекаются по окружностям aиb, концы диаметров(1-3 и 2-4) которых получаются при пересечении очерковых линий (главных меридианов).

Это свойство соосных поверхностей положено в основу способа вспомогательных секущих сфер.

3.3.5. Построение проекций линий пересечения поверхностей вращения с помощью вспомогательных сфер (концентрических). В этом способе при построении линии пересечения заданные поверхности пересекают сферами, соосными с данными поверхностями, причём центры всех вспомогательных сфер находятся в точке пересечения осей вращения.

Вспомогательная сфера пересекает каждую из заданных поверхностей по окружности. Эти окружности, расположенные на одной и той же сфере, будут пересекаться друг с другом. Точки пересечения окружностей принадлежат искомой линии пересечения.

Для применения этого способа необходимы следующие условия:

1) обе пересекающиеся поверхности являются поверхностями вращения;

2) оси вращения поверхностей должны пересекаться и располагаться в плоскости, параллельной одной из плоскостей проекций.

На рис 3.15 показано построение линии пересечения двух прямых круговых конусов Φ ∩Τ. Оси вращенияίиjпересекаются в точкеO (O₁ , O₂) и параллельны плоскостиΠ₂. Это и будет центр вспомогательных сфер.

При пересечении очерковых линий конусов получаются точки: A– самая высокая иB– самая низкая, принадлежащие искомой линии пересечения.

При пересечении двух конусов плоскостью Γ (Γ₂) получаем точкиCиD:δ₁∩n₁=C₁ иD₁, и на линии проекционной связи определяем точкиC₂ иD₂.

Далее необходимо отметить границы введения вспомогательных сфер.

Максимальный радиус вспомогательной сферы (R_max=O₂B₂) определяется расстоянием от точки пересечения осей до наиболее удалённой точки пересечения очерковых линий, а минимальный радиус сферыR_min равен радиусу сферыΣ, вписанной в наибольший из очерков поверхностей, т. е. в поверхностьΦ, касающейся её по окружностиm (m₁, m₂), и пересекающей другую поверхностьT по окружности3-4 (3₂-4₂). Плоскости этих окружностей перпендикулярны осям вращения поверхностей. При пересечении этих окружностей получаются точкиKи, принадлежащие линии пересечения поверхностей:Σ∩Φ=1-2, Σ∩T=3-4 и далее1-2∩3-4=K и (1₂-2₂∩3₂-4₂=K₂≡).

По такому же алгоритму с помощью промежуточных сфер строятся другие точки, принадлежащие линии пересечения,.

Радиусы промежуточных сфер берут произвольно в пределах между R_minиR_max.

На чертеже проведена одна из промежуточных сфер радиуса Rи построены точкиL (L₁, L₂)иN (N₁, N₂).

Проведя ещё несколько вспомогательных сфер, получим ряд точек, принадлежащих линии пересечения. Соединив одноимённые проекции полученных точек, получаем проекции линии пересечения. Затем определяем видимость линии пересечения и очерковых линий.