1.2.4. Свойства параллельных проекций.

Рассмотрим некоторые свойства параллельных проекций.

Точкав натуре проецируется в точку на плоскость проекций. Это свойство вытекает из правил построения в методе проекций.

Прямаяв натуре, в общем случае, проецируется в прямую на плоскость проекций. Если прямая направлена вдоль проецирующего луча, то ее проекцией будет точка.

Для того, чтобы спроецировать прямую, необходимо взять все ее точки и каждую спроецировать на плоскость проекций. Множество полученных проекций точек будет представлять собой проекцию прямой.

Возьмем на прямой АВ(рис. 1.7) точкиС¹,С²иС³и спроецируем их на плоскостьП_Nпараллельно некоторому заданному направлению. Образовавшееся множество лучей представляет собой плоскость, так как все лучи пересекают прямуюАВи остаются параллельными некоторому направлению.

П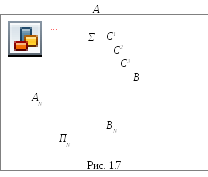лоскость, образованная проецирующими лучами, называетсяпроецирующей. Обозначим ее буквойΣ. При пересечении плоскостейΣиП_Nобразуется прямаяА_NB_N , которая является проекцией прямойАВ.

Инцидентность– взаимная принадлежность. Если точка лежит на прямой, то проекции точки лежат на проекциях прямой. Доказательство: пусть на прямойАВ(рис. 1.7) даны точкиС¹,С²иС³. Проецирующие лучи, проходящие через эти точки, лежат в проецирующей плоскостиΣи пересекаются с проекцией прямойА_NB_Nв точках,и, так какА_NB_N также лежит в плоскостиΣ.

Эти три свойства относятся также и к центральной системе проецирования.

Деление отрезка в данном отношении.Если точка делит отрезок в некотором отношении, то проекция точки делит проекцию отрезка в том же отношении. Доказательство: пусть точкаС¹(рис. 1.7) делит отрезокАВв отношении. Из рисунка видно, что прямаяАВи ее проекцияА_NB_Nлежат в одной проецирующей плоскостиΣи пересекаются.

Проецирующие лучи АА_N,С¹СиВВ_Nпараллельны. Известно, что параллельные прямые отсекают на пересекающихся прямых пропорциональные части, следовательно.

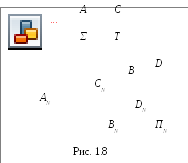
Проекции параллельных прямых. Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 1.8). Доказательство: прямыеАВиCDпроецируются с помощью проецирующих плоскостейΣиТ, ноΣ║Т, т. к.АВ║CDпо условию иАА_N║СС_N - по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскостиΣиТпересекаются плоскостью проекцийП_Nи образуются параллельные прямые (А_NВ_N║C_ND_N).

П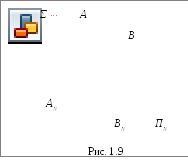роекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура - прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: даноΣ║П_NиАВΣ(рис. 1.9). Требуется доказать, чтоАВ║А_NВ_N иАВ=А_NВ_N. Так какΣ║П_N , то отрезкиАА_NиВВ_N равны и параллельны. Следовательно, четырехугольникАВВ_NА_Nявляется параллелограммом иАВ║А_NВ_N,АВ=А_NВ_N.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

Частный случай проецирования прямого линейного угла.Если плоскость угла не параллельна плоскости проекций, то в общем случае угол проецируется с искажением.

В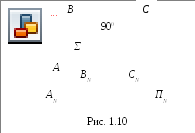частном случае для ортогонального проецирования имеет место следующее:если одна сторона прямого линейного угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол проецируется в натуральную величину (рис. 1.10).При этом плоскость угла не параллельна плоскости проекций. Доказательство: даноАВВС;ВС║П_N;АВ╫П_N. Требуется доказать, чтоВ_NС_NА_NВ_N.

Пусть АВпроецируется с помощью плоскостиΣ, аВС- с помощью плоскостиТ, тогда:

1) ВСΣ, так какВСАВпо условию иВСВВ_Nпо построению;

2) В_NС_NΣ, так какВ_NС_N║ВСиВСΣ;

3) В_NС_NА_NВ_N, так как если прямая перпендикулярна к плоскости, то она перпендикулярна любой прямой, лежащей в плоскости.

1.2.5.Проецирующие геометрические фигуры.Это геометрические фигуры, образованные проецирующими лучами. Проецирующими геометрическими фигурами могут быть:

- прямые - проецируют точки;

- плоскости - проецируют прямые линии и плоские фигуры;

- цилиндрические поверхностив параллельной системе проецирования иконические поверхностив центральной системе проецирования - проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следомданной проецирующей геометрической фигуры или ееглавной проекцией.

На рис. 1.11 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскостьΣи проецирующая цилиндрическая поверхностьФ.

П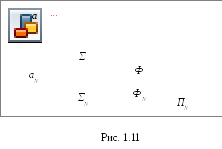рямаяа, плоскостьΣи образующие цилиндрической поверхностиФперпендикулярны плоскости проекцийП_N . Их главные проекцииа_N ,Σ_NиФ_Nвключают в себя проекции всех точек данной проецирующей геометрической фигуры.

1.2.6. Дополнения однокартинного чертежа.Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок.Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 1.12 даны проекции различных геометрических фигур с числовыми отметками.

П_N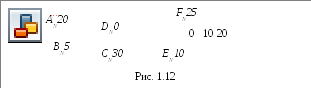

Около проекции точки Астоит цифра 20. Это означает, что точкаАотстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВСотстоят от плоскости на расстояниях 15 и 30, вершины треугольникаDEF - на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость П_Nгоризонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскостиП_N.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Способ применения двух плоскостей проекций. Точка проецируется на две плоскости проекцийП₁иП₂(рис. 1.13). При ортогональном проецировании принято располагать плоскости проекций перпендикулярно друг другу (П₁П₂).

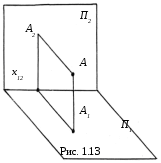Проекция точки на каждой плоскости проекций обозначается той же буквой, что и сама точка, но с индексом данной плоскости проекций. Так, проекция точкиАна плоскостьП₁обозначаетсяА₁.

Линия пересечения плоскостей проекций обозначается буквой х, около которой ставятся индексы плоскостей, линией пересечения которых она является, т.е.х₁₂.

Вторая плоскость проекций П₂является дополнением однокартинного чертежа наП₁. Если даны проекции точекА₁иА₂наП₁иП₂, то всегда можно определить положение точки в пространстве на пересечении перпендикуляров, восстановленных к плоскостям проекций из этих точек.

Таким образом, проекции точки на две взаимноперпендикулярные плоскости проекций дают полное представление о положении точки в пространстве. Способ дополнения однокартинного чертежа с помощью второй плоскости проекций в настоящее время принят в технике как основной.