3.5. Перпендикулярные геометрические объекты

3.5.1. Перпендикулярные прямые.На рис. 3.24 показано построение прямойℓ, проходящей через точкуA и перпендикулярной прямойa.

Прямая a - горизонталь, то естьa||Π₁.

Из теоремы о частном случае проецирования прямого линейного угла (см. рис. 1.10) следует, что если одна сторона прямого линейного угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол спроецируется в натуральную величину.

Следовательно, через A₁проводимℓ_1┴ a₁, отмечаем точкуK₁, находимK₂ по линии проекционной связи наa₂ и проводимℓ₂, то естьℓ_1┴ a₁ так какa||Π₁ иℓ_┴ a(рис. 3.24).

3.5.2. Перпендикулярные прямая и плоскость. Как известно,прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости.

При построениях удобно применять в качестве пересекающихся прямых горизонтальhи фронтальf.

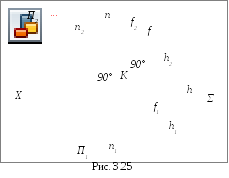
Пусть необходимо (рис. 3.25) из точки KΣ восставить перпендикулярn  Σ.

Для этого через точку K проведём горизонтальh и фронтальf и перпендикулярно к ним проведём прямуюn (n_┴ h и n_┴ f).

На основании теоремы о частном случае проецирования прямого линейного угла угол между nиhнаΠ₁ спроецируется без искажения, то есть угол между горизонтальной проекцией горизонталиh₁и горизонтальной проекцией перпендикуляраn₁будет прямым (n_1┴ h₁).

Аналогичным образом можно доказать, что если n_┴ f, тоn_2┴ f₂, где

f₂ – фронтальная проекция фронтали.

Следовательно, если прямая перпендикулярна к плоскости, то её проекции перпендикулярны к одноимённым проекциям одноимённых линий уровня, то есть еслиn_┴ Σ (h∩f), тоn_1┴ h₁иn_2┴ f₂.

Пусть требуется из точки K(K₁, K₂) восстановить перпендикуляр к плоскостиΣ (a||b) (рис. 3.26,а).

На рис. 3.26,б показано построение такого перпендикуляра.

В плоскости Σпроведены горизонтальh (h₁, h₂) и фронтальf (f₁, f₂).

Через точку K₁проведенаn_1┴ h₁и через точкуK₂ проведенаn_2┴ f₂.

3.5.3. Перпендикулярные плоскости. Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую линию, перпендикулярную другой. Поэтому при проведении плоскости, перпендикулярной к другой плоскости, сначала строят прямую, перпендикулярную к плоскости, и затем заключают её в какую-либо плоскость.

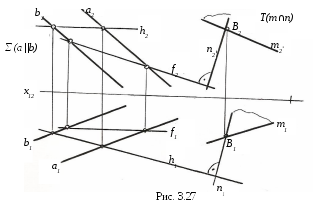
На рис. 3.27 через точку Bпроведена плоскостьT(m∩n) перпендикулярноΣ (a||b).

Для этого в плоскости Σ (a||b) построены горизонтальh (h₁, h₂) и фронталь f (f₁, f₂).

Затем через точку Bпроводимn_┴Σ, то естьn_1┴ h₁,n_2┴ f₂. Прямуюm (m₁, m₂) через точкуB (B₁ , B₂) проводим произвольно.

Построенная плоскость T (m∩n) будет перпендикулярнаΣ.

4. Аксонометрические проекции

4.1. Образование и виды аксонометрических проекций

Проекция предмета вместе с заданной системой координат на одну плоскость называется аксонометрической проекцией или аксонометрией. Плоскость проекций в этом случае называется аксонометрической. Наиболее часто применяется параллельное аксонометрическое проецироввание.

Образование аксонометрической проекции рассмотрим на примере построения аксонометрии точки В, отнесённой к натуральной системе координатxyz (рис. 4.1). ЗдесьП_А – аксонометрическая плоскость проекций,s – направление проецирующих лучей, В_А – аксонометрическая проекция точкиВ;x_A,y_A,z_A– аксонометрические проекции осей координатx,y,z; эти проекции также называются аксонометрическими координатными осями.

При аксонометрическом проецировании происходит искажение линейных размеров проецируемых объектов, которое характеризуется коэффициентами искаженияпо направлениям вдоль координатных осей. Коэффициент искажения по осих определяется отношением длины аксонометрической проекции отрезка, отложенного вдоль этой оси, к натуральной величине этого отрезка:к=О_АЕ_А /ОЕ. Аналогично определяются коэффициенты искажения по осямyиz– соответственно величиныmиn.

z_B

x_В

y_В

В зависимости от положения аксонометрической плоскости проекций П_А относительно координатной системыxyz аксонометрические осиx_A,y_A,z_Aмогут занимать различные положения, а коэффициенты искажения принимают различные значения. Аксонометрические проекции, в которыхk =m =n, называютсяизометрическими; если k =n ≠m –диметрическими; еслиk ≠m ≠n–триметрическими.

Аксонометрические проекции также различают в зависимости от угла наклона проецирующих лучей s к аксонометрической плоскости проекцийП_А. ЕслиsП_А , аксонометрическая проекция называетсяпрямоугольной; если проецирующие лучи не перпендикулярны аксонометрической плоскости, аксонометрическая проекция называется косоугольной.

Аксонометрические проекции, рекомендуемые к применению при выполнении чертежей, включены в Государственный стандарт ГОСТ 3.317-69 «Аксонометрические проекции» Единой системы конструктрской документации. Далее рассмотрим эти проекции подробнее.