1. Метод проекций
1.1. Основные понятия и определения
Методом проекций в начертательной геометрии называют способ, посредством которого получают изображения геометрических фигур. При этом начертательная геометрия рассматривает лишь их геометрические свойства.
1.1.1. Геометрические фигуры. К геометрическим фигурам, подлежащим изучению, относятся абстрактные точки, прямые и кривые линии, поверхности и геометрические тела.
Точка представляет собой абстрактное понятие, не имеющее измерений. Можно говорить только о положении точки в пространстве.
Линия(прямая или кривая) состоит из множества точек, не имеет толщины и имеет лишь одно измерение. Можно говорить о положении линии в пространстве и о ее длине.
Поверхность(плоскость, цилиндрическая и коническая поверхности, сфера и др.) представляет собой множество точек или множество линий, не имеет толщины и имеет два измерения вдоль поверхности. Можно говорить о положении поверхности в пространстве и ее размерах.
Пространственные геометрические теламогут быть ограничены точками, линиями и поверхностями.
В конечном счете каждое геометрическое тело (точнее, поверхность, ограничивающая тело) может быть представлено множеством точек.
Поэтому, прежде чем перейти к изображению пространственных тел, изучим законы изображений с помощью точки.
1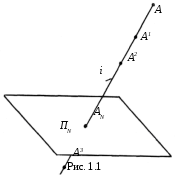
.1.2.
Элементы и особенности метода проекций.
Процесс проецирования заключается
в проведении через выбранную точкуАизображаемой геометрической фигуры
проецирующего лучаi(прямая линия) до пересечения в точкеАNс некоторой
плоскостью проекцийПN.
ТочкаАNявляется проекцией (изображением) точкиАна плоскостиПN
(рис. 1.1).
Таким образом, имеем четыре элемента метода проекций: пространственая точка -А;проецирующий луч -i;плоскость проекций(картинная плоскость, плоскость изображений) -ПN ;проекция точки(изображение точки) –АN , (обозначается той же буквой, что и пространственная точка, но с индексом плоскости проекций). Операция получения проекции точки называетсяпроецированием.
Из рис. 1.1 вытекают две особенности метода проекций.
Первая особенность заключается в том, что каждой пространственной точке А1,А2,А3, расположенной на данном проецирующем лучеi, соответствует только одна точкаАNплоскости проекцийПN , т. е.
.
С другой стороны, каждой точке АN плоскости проекцийПNсоответствует бесчисленное множество точекА1,А2,А3, … , расположенных на проецирующем лучеi, проходящем через данную точкуАN , т. е.
АN→
Аn
i.
Эти особенности наглядны и не нуждаются в специальном доказательстве.
Из второй особенности вытекает, что одной проекции точки недостаточна для определения положения самой точки в пространстве. Можно сказать, что изображение точки на одной плоскости проекций является неполным. По одному изображению невозможно представить себе место расположения точки в пространстве.
Ниже мы познакомимся со способами получения полных изображений точки, по которым можно будет определить ее положение в пространстве.
Точки, расположенные на одном проецирующем луче, называются конкурирующими.