3. Позиционные задачи
Это задачи, в которых решается вопрос о взаимном порядке, взаимном положении и взаимном пересечении геометрических объектов.
Задачи на взаимный порядок и взаимное положение геометрических объектов, а также задачи на взаимную принадлежность геометрических объектов были разобраны в разделах 1 и 2. Эти задачи не имеют самостоятельной методики и опираются на решение других позиционных задач. Наибольший практический интерес представляютзадачи на пересечение поверхностейизадачи на пересечение линии и поверхности.Изучение этих задач рассмотрим методом индукции, т. е. от частного к общему.
В этих двух типах задач можно выделить три группы задач:
1) Оба пересекающихся геометрических объекта занимают проецирующее положение;
2) Один из пересекающихся геометрических объектов занимает проецирующее положение, другой – непроецирующее;
3) Оба пересекающихся геометрических объекта занимают непроецирующие положения.
Проецирующими геометрическими объектами могут быть: прямая, плоскость, цилиндрическая поверхность (см. рис. 1.11).
Рассмотрим первый тип задач – задачи на пересечение поверхностей.
Вначале рассмотрим задачи на пересечение проецирующих геометрических объектов и когда один из объектов непроецирующий. После этого рассмотрим задачи на построение линии пересечения непроецирующих геометрических объектов.
3.1. Пересечение геометрических объектов, когда оба геометрических объекта проецирующие
3
.1.1.
Построение линии пересечения двух
горизонтально-проецирующих плоскостей.На рис. 3.1 заданы горизонтально-проецирующие
плоскостиΣиΤ. Так как обе
плоскости горизонтально-проецирующие,
то и линия их пересечения ℓтакже
является горизонтально-проецирующей
прямой, т. е.Σ ∩Τ=ℓ, Σ┴Π1
иΤ┴Π1 ,
следовательно,ℓ┴Π1.
3.1.2. Виды линий пересечения прямого кругового цилиндра с плоскостями. Такими линиями являются:
- окружность,когда секущая плоскостьΤперпендикулярна оси цилиндра;
- две параллельные прямые,если плоскостьΩ параллельна оси цилиндраί;
-
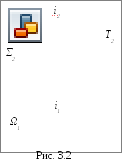эллипс– в любом другом положении
секущей плоскостиΣ (рис. 3.2).
На рисунке 3.3 дано построение проекций и натуральной величины линии пересечения (эллипс) прямого кругового цилиндра с плоскостью Σ. На плоскостьΠ2 эллипс проецируется в виде отрезка, совпадающего сΣ2, наΠ1 – в виде окружности.
Таким образом, фронтальная и горизонтальная проекции линии пересечения на чертеже в данном случае уже очевидны (определены). Натуральная величина эллипса построена по точкам с помощью введения дополнительной плоскости Π5 ;х25||Σ2, т.е.Π5||Σ иΠ5┴ Π2.
3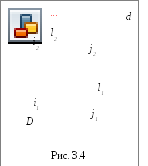
.1.3.
Определение проекций линии пересечения
двух круговых цилиндров.На рис. 3.4
осьί одного цилиндра задана
перпендикулярноΠ1, ось
jдругого цилиндра перпендикулярнаΠ2, т. е. обе поверхности
являются проецирующими.
Следовательно, фронтальная проекция линии пересечения цилиндров ℓ (ℓ2) совпадает с фронтальной проекцией боковой поверхности цилиндра с осьюj (окружностью диаметраd), а горизонтальная проекцияℓ (ℓ1) совпадает с горизонтальной проекцией боковой поверхности цилиндра с осьюi (окружностью диаметраD).
Проекции линии пересечения ℓ (ℓ1,ℓ2) должны находиться внутри очерков поверхностей.
Итак, когда оба пересекающихся геометрических объекта проецирующие, то проекции линии пересечения на чертеже уже заданы, их надо только отметить.