Задания для самостоятельной работы

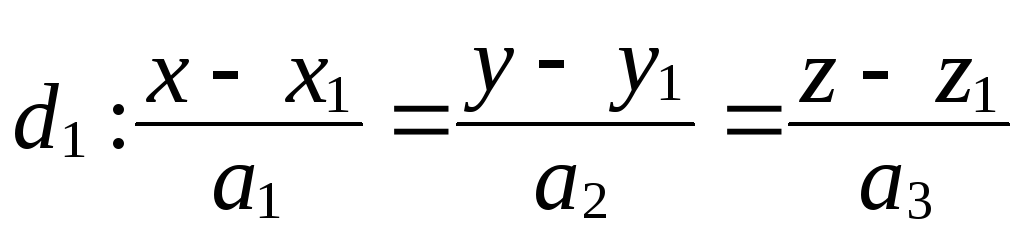1. Запишите в координатном виде условие того, что прямые и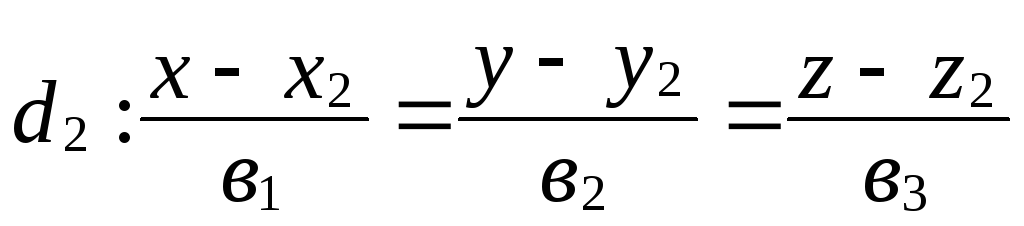являются скрещивающимися.

2. Запишите в координатном виде условие того, что прямые и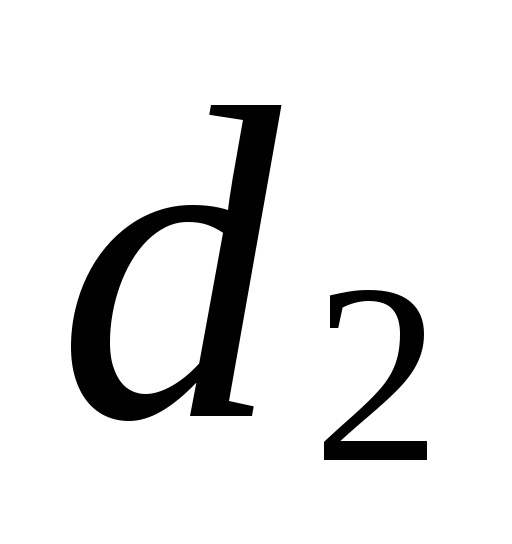(см. задание 1) пересекаются.

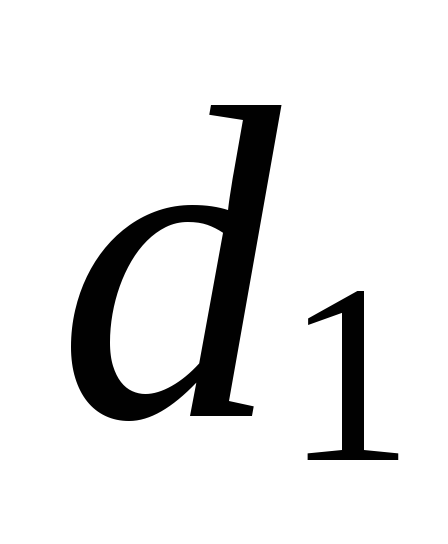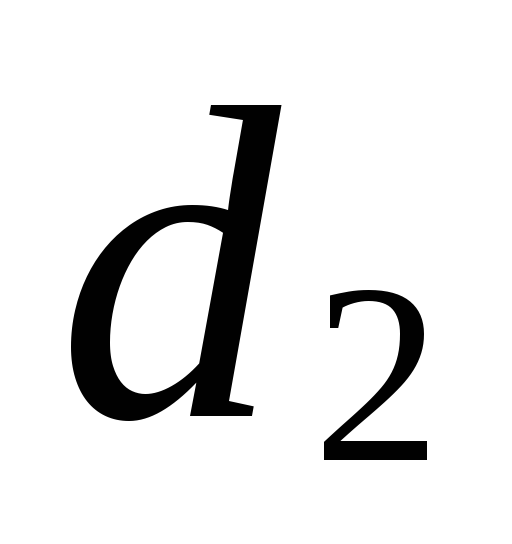3. Запишите в координатном виде условие параллельности прямых и(см. задание 1).

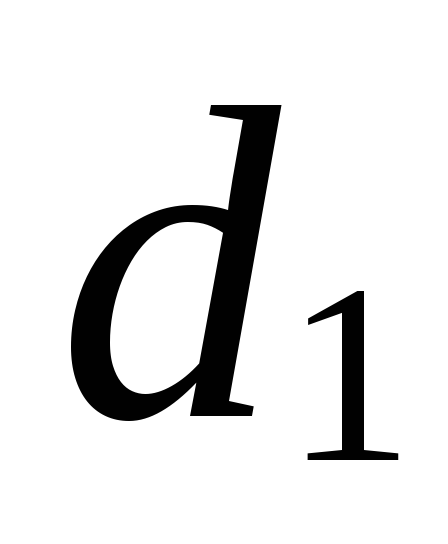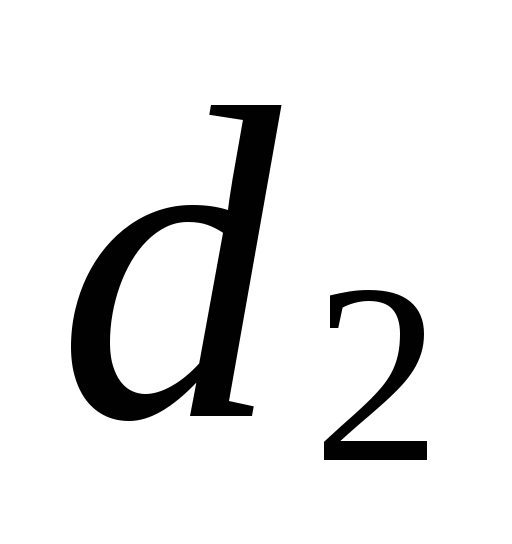4. Запишите в координатном виде условие совпадения прямых и(см. задание 1).

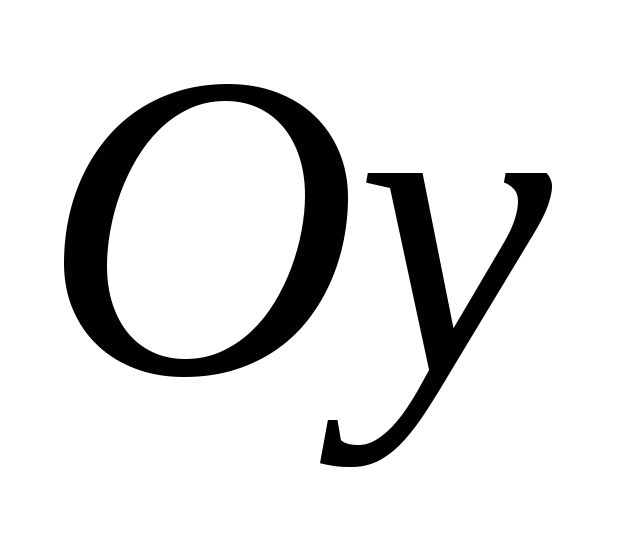5. Выясните взаимное расположение прямой и оси: а); б); в)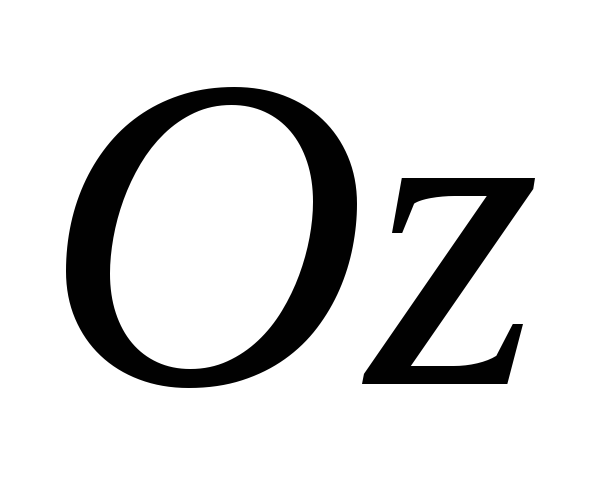аффинной системы координат.

6. Выясните взаимное расположение прямой и координатной плоскости: а); б); в).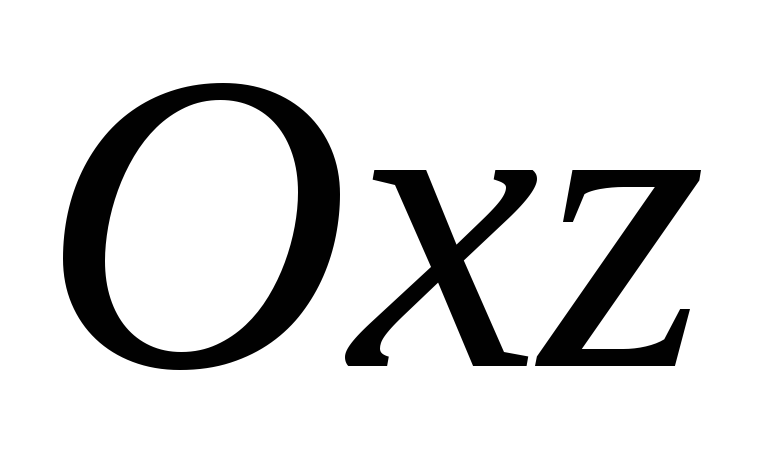

§ 27. Основные метрические задачи на прямые и плоскости в пространстве

1. Угол между двумя прямыми в пространстве.

Возьмем в пространстве две непараллельные прямые и. Тогдаиявляются либо пересекающимися, либо скрещивающимися. Еслиипересекаются, то они образуют четыре угла. Тогдауглом между иназывается тот из четырех углов, который по величине не превосходит остальные.

Пустьиявляются скрещивающимися. Возьмем в пространстве произвольную точкуи проведем через нее прямыеи(рис. 83). Прямыеиобразуют четыре угла с вершиной. Тот из них, который по величине не превосходит остальные, называетсяуглом между прямыми и.

Выведем формулу для вычисления косинуса угла между прямыми и. Пустьи направляющие векторы прямых исоответственно. Возможны два случая:

а) Если , то. Тогда.

б) Если , то. Тогда.

Из пунктов а), б) следует, что . Таким образом,

. (35)

2. Условие перпендикулярности двух прямых в пространстве.

Из формулы (35) получаем:

.

Итак,

(две прямые в пространстве взаимно перпендикулярны тогда и только тогда, когда скалярное произведение их направляющих векторов равно нулю).

Заметим, что взаимно перпендикулярные прямые в пространстве могут быть как пересекающимися, так и скрещивающимися.

3. Угол между прямой и плоскостью.

Напомним, что прямая называетсяперпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.

Если не перпендикулярна, тоуглом между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость(рис. 84).

Если , тоугол между исчитается равным.

Пусть ине перпендикулярна, направляющий вектор прямой , а плоскостьзадана в прямоугольной декартовой системе координат общим уравнением. Найдем величину угламежду прямойи плоскостью. Положим.

Возможны два случая:

а) Если (рис. 85, а), то.

б) Если (рис. 85, б), то

.

Из пунктов а), б) следует, что . Учитывая, что, получаем:

. (36)

Заметим, что если , то, тогда(соответственные координаты коллинеарных векторов пропорциональны). Тогда левая часть формулы (36) будет равна:

,

а правая – .

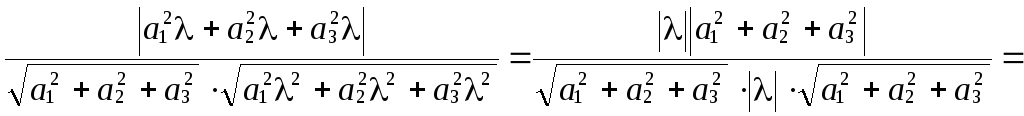
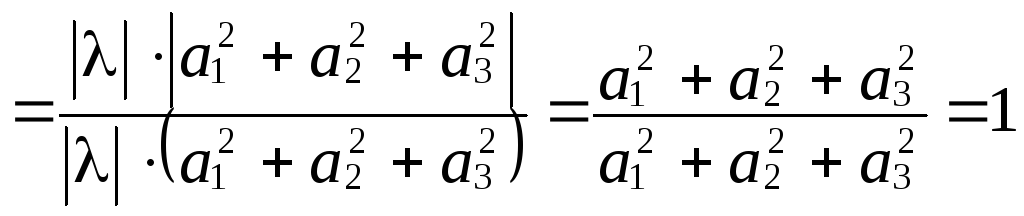Таким образом, если , то формула (36) также справедлива.

4. Условие перпендикулярности прямой и плоскости.

. Применяя условие коллинеарности двух векторов в координатах, получим:

.

Задания для самостоятельной работы

1. Укажите на чертеже угол между ребром кубаи диагональюего грани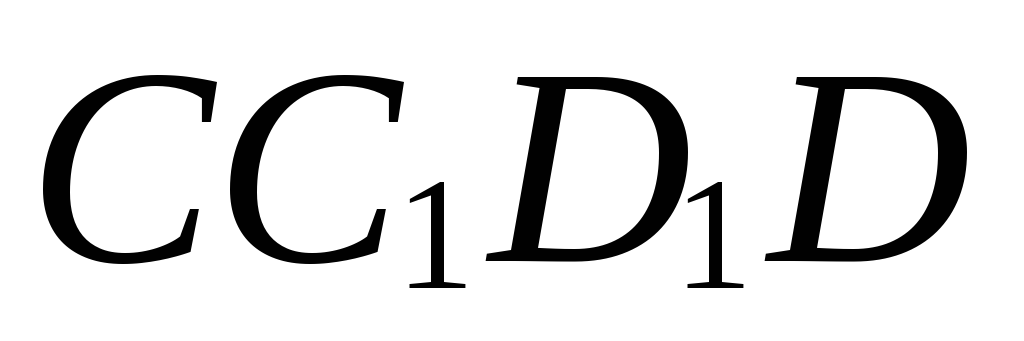; угол между ребрамии.

2. Вычислите величину угла между прямой и осью абсцисс прямоугольной декартовой системы координат.

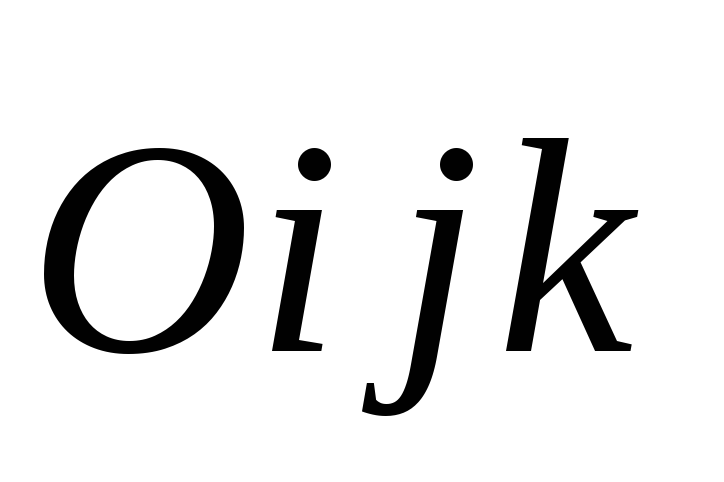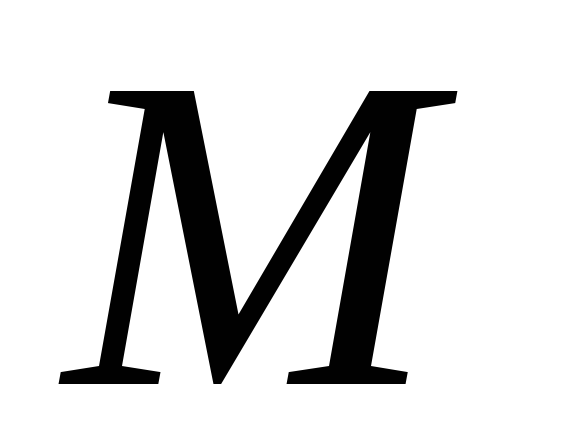3. –середина ребр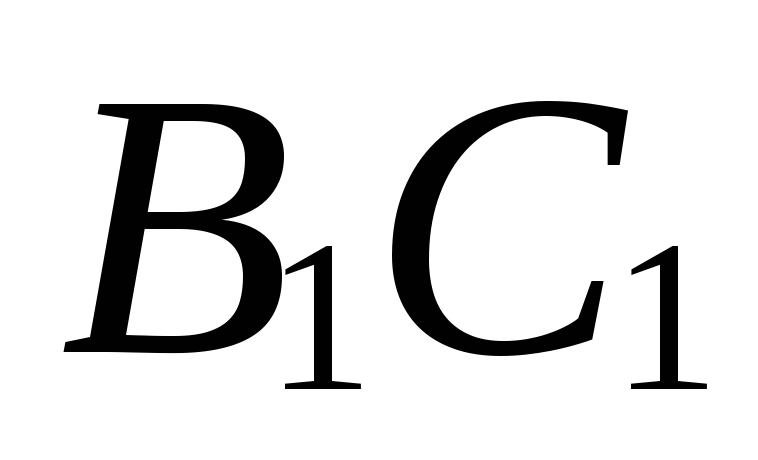а куба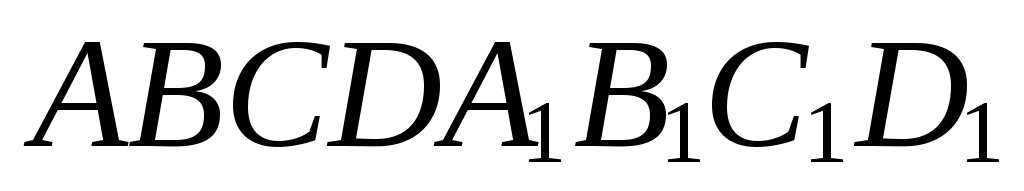. Укажите на чертеже угол между прямойи плоскостьюнижнего основания куба.

4. Вычислите величину угла между прямой и координатной плоскостью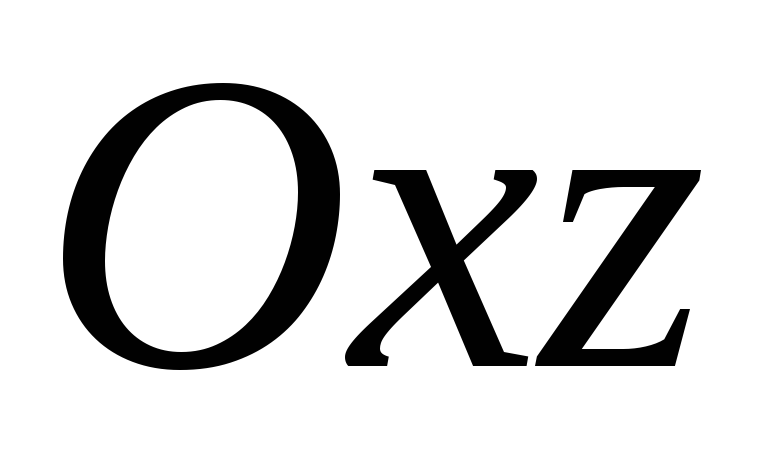прямоугольной декартовой системы координат.

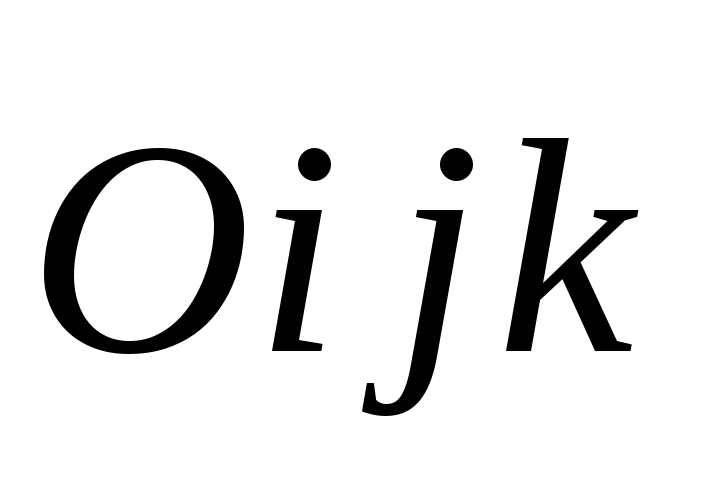5. Выясните, будет ли прямая 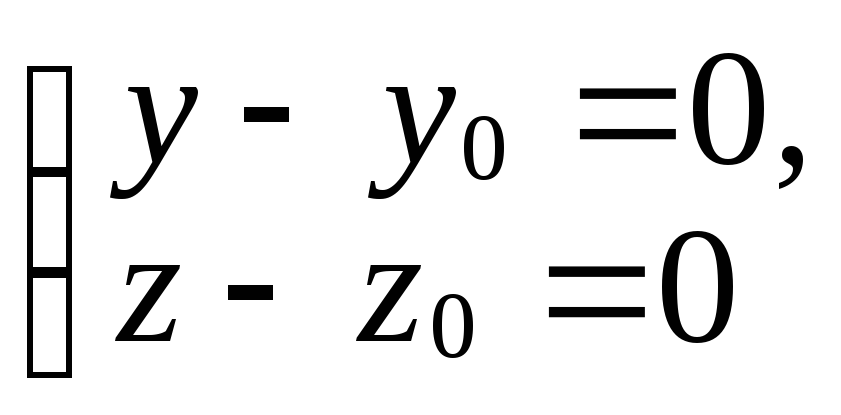перпендикулярна плоскостипрямоугольной декартовой системы координат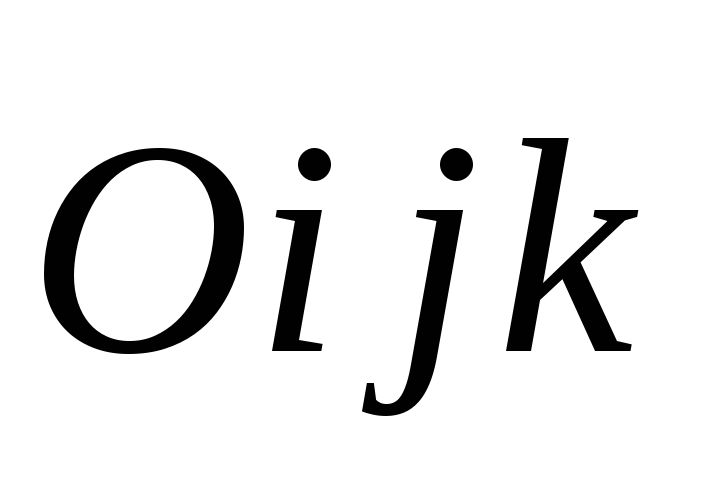.