
- •Кафедра алгебры, геометрии, теории и методики обучения математике
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •Свойства умножения вектора на число
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •Применение векторного произведения
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •Лекция 10
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§ 22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости
- •Задания для самостоятельной работы
- •§ 23. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§ 24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§ 25. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§ 26. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§ 27. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
Задания для самостоятельной работы
1. Какие из векторов
![]() параллельны плоскости
параллельны плоскости![]() и почему?
и почему?
2. Справедливы ли утверждения, доказанные в пунктах 1-13, если уравнение плоскости задано в прямоугольной декартовой системе координат и почему?
3. Составьте
уравнение плоскости, проходящей через
точку
![]() и параллельной плоскости: а)
и параллельной плоскости: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() (пользуясь частными случаями общего
уравнения плоскости).
(пользуясь частными случаями общего
уравнения плоскости).
4. Составьте
уравнение плоскости, которая проходит
через точку
![]() и содержит: а) ось
и содержит: а) ось![]() ;
б) ось
;
б) ось![]() ;
в) ось
;
в) ось![]() (пользуясь частными случаями общего
уравнения плоскости).
(пользуясь частными случаями общего
уравнения плоскости).
§ 23. Основные аффинные задачи, связанные с плоскостью (обзор)
1. Взаимное расположение двух плоскостей.
Выяснить взаимное расположение двух плоскостей позволяет следующая теорема:
Теорема 1.
Пусть в аффинной системе координат
![]() плоскости
плоскости![]() и
и![]() заданы общими уравнениями:
заданы общими уравнениями:
![]() ,
,
![]() .
.
![]() или
или
![]() ;
;
![]() (коэффициенты при
х,
у,
z
пропорциональны, а свободные члены им
не пропорциональны);
(коэффициенты при
х,
у,
z
пропорциональны, а свободные члены им
не пропорциональны);
![]() .
.
2. Взаимное расположение трех плоскостей.
Вопрос о взаимном
расположении трех плоскостей
![]() ,
,![]() и
и![]() сводится к исследованию вопроса о
взаимном расположении трех пар плоскостей:
сводится к исследованию вопроса о
взаимном расположении трех пар плоскостей:![]() и
и![]() ,
,![]() и
и![]() ,
,![]() и
и![]() .
.
Возможны восемь случаев взаимного расположения этих плоскостей:
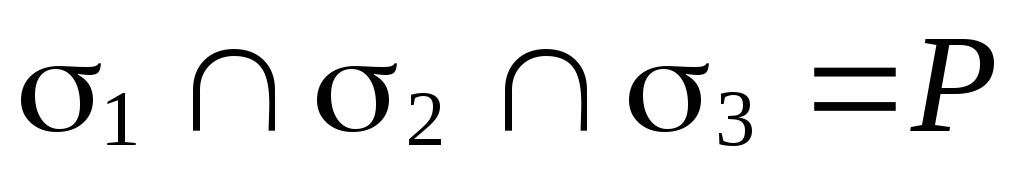 (рис. 70, а);
(рис. 70, а);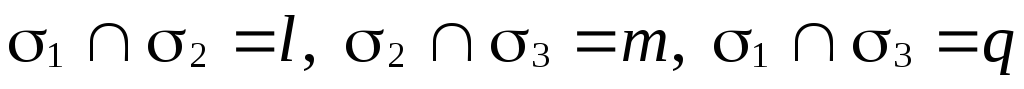 (рис. 70, б);
(рис. 70, б);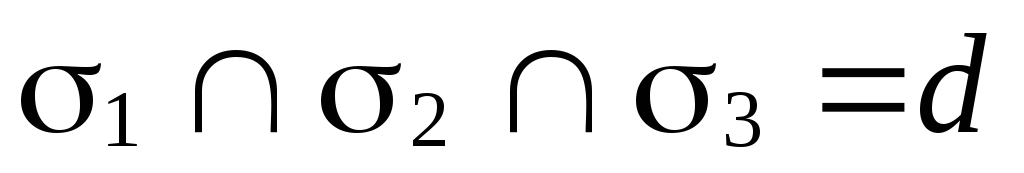 (рис. 70, в);
(рис. 70, в); (следовательно,
(следовательно,
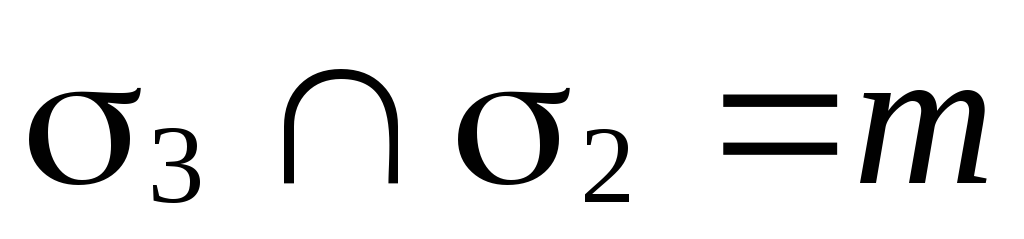 )
(рис. 70, г);
)
(рис. 70, г);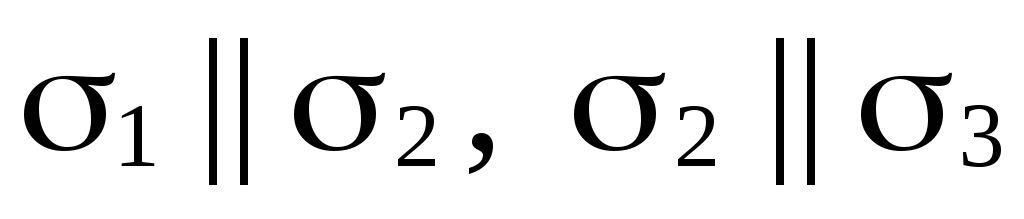 (следовательно,
(следовательно,
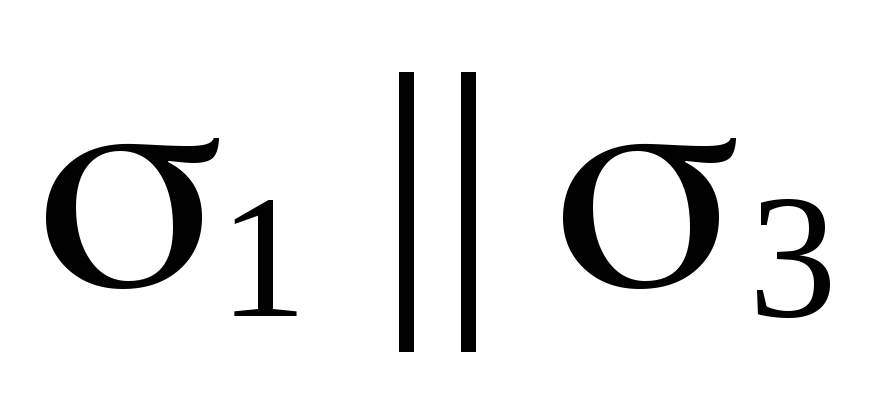 )
(рис. 70, д);
)
(рис. 70, д); (рис. 70, е);
(рис. 70, е);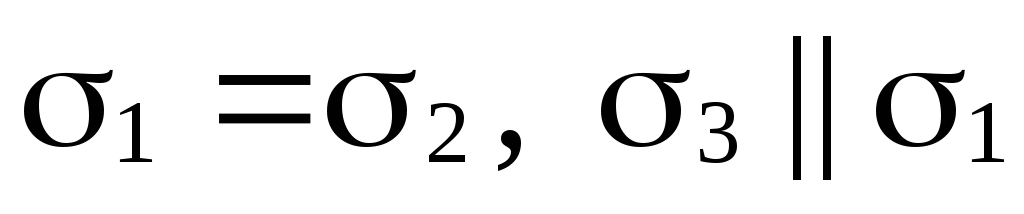 (рис. 70, ж);
(рис. 70, ж);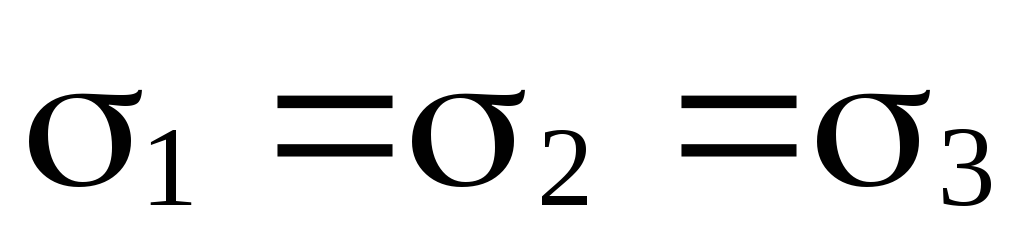 (рис. 70, з).
(рис. 70, з).
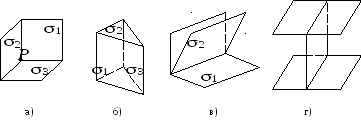
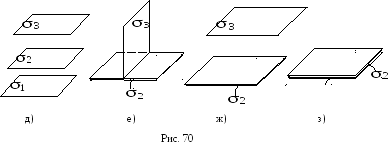
3. Геометрический
смысл знака многочлена
![]() .
.
Теорема 2.
Если в аффинной системе координат
плоскость
![]() задана уравнением
задана уравнением
![]() ,
то два полупространства, на которые эта
плоскость разбивает пространство,
определяются условиями
,
то два полупространства, на которые эта
плоскость разбивает пространство,
определяются условиями
![]() и
и
![]() .
.
4. Пучок и связка плоскостей.
Пучком плоскостей
называется
множество всех плоскостей, проходящих
через одну и ту же прямую
![]() .
Прямая
.
Прямая![]() называетсяосью
этого пучка.
называетсяосью
этого пучка.
Пусть
![]() .
Тогда уравнение пучка плоскостей с осью
.
Тогда уравнение пучка плоскостей с осью![]() имеет вид:
имеет вид:
![]() ,
где
,
где
![]() не равны нулю одновременно.
не равны нулю одновременно.
Связкой плоскостей
называется множество всех плоскостей,
проходящих через одну и ту же точку
![]() .
Точка
.
Точка![]() называетсяцентром
связки.
называетсяцентром
связки.
Пусть
![]() .
Тогда уравнение связки плоскостей имеет
вид:
.
Тогда уравнение связки плоскостей имеет
вид:
![]() ,
где
,
где
![]() и
и![]() не равны нулю одновременно.
не равны нулю одновременно.
Задания для самостоятельной работы
Пользуясь теоремой 1 из § 22, выведите уравнение плоскости, параллельной плоскости
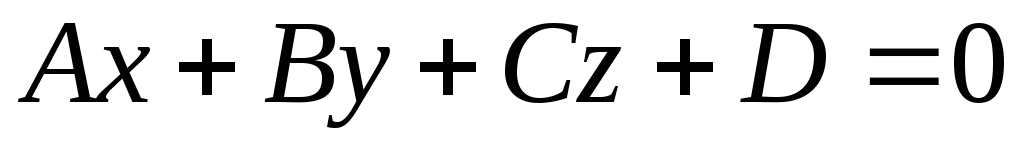 и проходящей через начало координат.
и проходящей через начало координат.Найдите уравнение плоскости, параллельной плоскости
 и проходящей через точку
и проходящей через точку
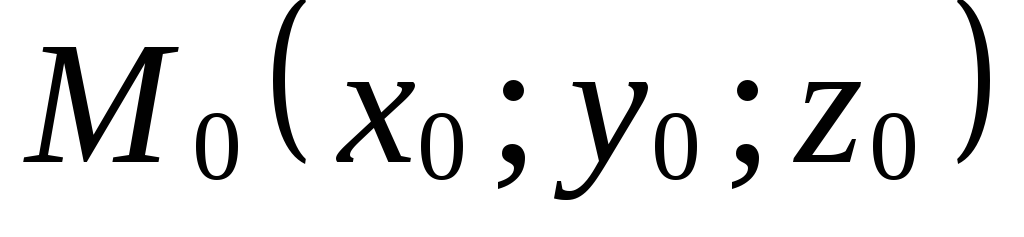 .
.В аффинной системе координат задана плоскость
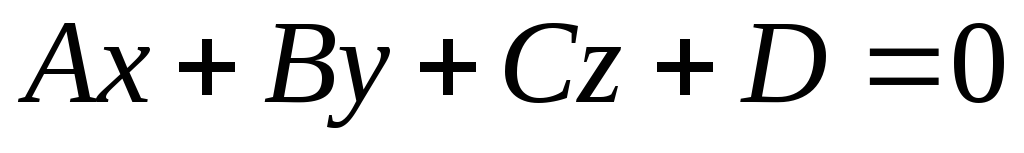 .
Какая фигура определяется условием:
а)
.
Какая фигура определяется условием:
а)
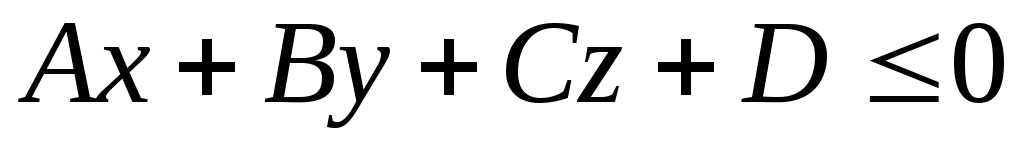 ;
б)
;
б)
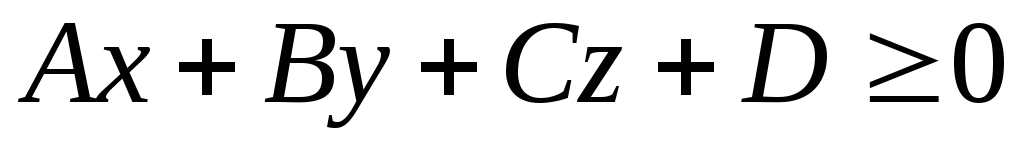 ?
?Верно ли утверждение, что плоскость
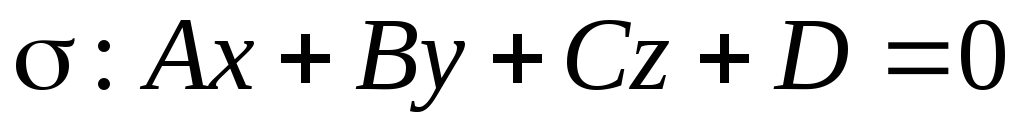 пересекает отрезок
пересекает отрезок
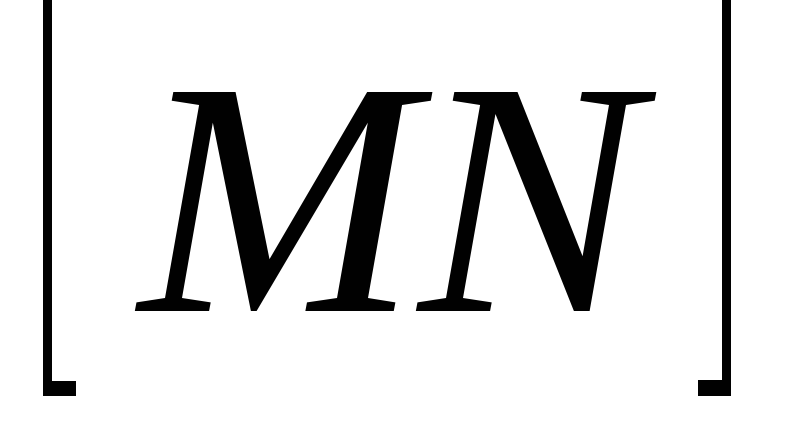 ,
где
,
где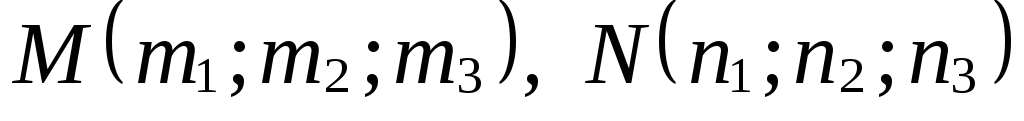 ,
тогда и только тогда, когда
,
тогда и только тогда, когда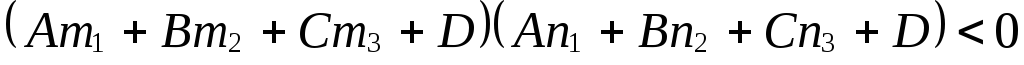 и почему?
и почему?Составьте уравнение плоскости, проходящей через начало координат и содержащей линию пересечения плоскостей
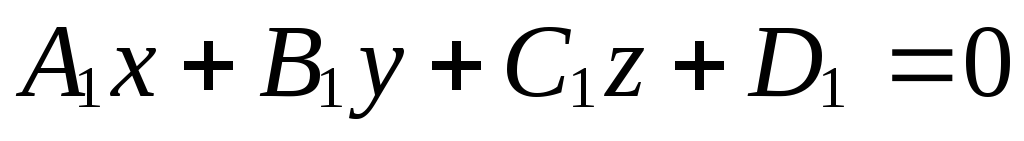 и
и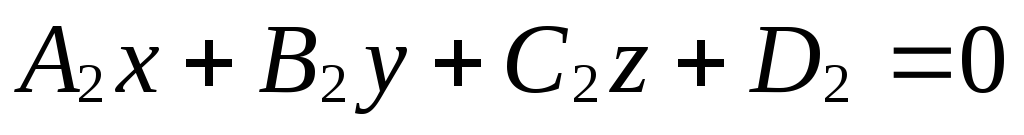 .
.
Лекция 12 Плоскость в прямоугольной системе координат
§ 24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью
1. Уравнение плоскости, заданной точкой и вектором нормали.
Ненулевой вектор называется перпендикулярным плоскости, если он ортогонален любому вектору, параллельному этой плоскости или лежащему в ней.
Вектор, перпендикулярный плоскости, называется вектором нормали этой плоскости или ее нормальным вектором.
Вектор нормали
плоскости
![]() будем обозначать через
будем обозначать через![]() .
.
Пусть в пространстве
дана прямоугольная декартова система
координат
![]() ,
плоскость
,
плоскость![]() ,
,![]() и
и![]() .
.
![]() (рис. 71).
(рис. 71).
Переходя к координатам, получаем уравнение
![]() .
(27)
.
(27)
Уравнение (27) называется уравнением плоскости, заданной точкой и вектором нормали.
С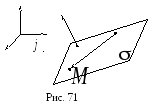 ледовательно,
коэффициентыА,
В
и С
при х,
у
и z
в общем уравнении плоскости, заданном
в прямоугольной декартовой системе
координат, имеют следующий геометрический
смысл: А,
В
и С
есть координаты вектора нормали данной
плоскости.
ледовательно,
коэффициентыА,
В
и С
при х,
у
и z
в общем уравнении плоскости, заданном
в прямоугольной декартовой системе
координат, имеют следующий геометрический
смысл: А,
В
и С
есть координаты вектора нормали данной
плоскости.
2. Расстояние от точки до плоскости.
Пусть в пространстве
дана плоскость
![]() и не принадлежащая ей точка
и не принадлежащая ей точка![]() .
Расстоянием от точки
.
Расстоянием от точки![]() до плоскости
до плоскости![]() называется длина перпендикуляра
называется длина перпендикуляра![]() ,
проведенного из точки
,
проведенного из точки![]() к плоскости
к плоскости![]() (рис. 72):
(рис. 72):![]() .
Если
.
Если![]() ,
то
,
то![]() .
.
П усть
в прямоугольной декартовой системе
координат
усть
в прямоугольной декартовой системе
координат![]() дано уравнение плоскости
дано уравнение плоскости![]() и точка
и точка![]() ,
не принадлежащая плоскости
,
не принадлежащая плоскости![]() .
Тогда расстояние от точки
.
Тогда расстояние от точки![]() до плоскости
до плоскости![]() вычисляется по формуле:
вычисляется по формуле:
![]() .
.
Доказательство этой формулы аналогично доказательству формулы для вычисления расстояния от точки до прямой на плоскости.
3. Расстояние между двумя параллельными плоскостями.
Пусть две
параллельные плоскости
![]() и
и![]() заданы в прямоугольной декартовой
системе координат
заданы в прямоугольной декартовой
системе координат![]() уравнениями
уравнениями![]() и
и![]() соответственно. Выведем формулу для
вычисления
соответственно. Выведем формулу для
вычисления![]() .
.
Заметим, что
![]() ,
где
,
где![]() .
Пусть
.
Пусть![]() .
Так как
.
Так как![]() ,
то
,
то![]() .
Поэтому
.
Поэтому![]() .
Итак,
.
Итак,
![]() .
.
4. Угол между двумя пересекающимися плоскостями.
Пусть
![]() в прямоугольной декартовой системе
координат
в прямоугольной декартовой системе
координат![]() .
.
Две пересекающиеся
плоскости образуют четыре двугранных
угла. Углом
между двумя пересекающимися плоскостями
будем называть тот из четырех двугранных
углов, который по величине не превосходит
остальные. Величину линейного угла
этого двугранного угла будем обозначать
через
![]() .
.
Выведем формулу
для вычисления косинуса угла между
плоскостями
![]() и
и![]() .
.
Пусть
![]() и
и![]()
векторы нормалей плоскостей
векторы нормалей плоскостей
![]() и
и![]() .
Зная величину угла
.
Зная величину угла![]() ,
можно вычислить величину угла
,
можно вычислить величину угла![]() .
При этом возможны два случая:
.
При этом возможны два случая:
а) Если
![]() (рис. 73, а), то
(рис. 73, а), то![]() ,
следовательно,
,
следовательно,![]() .
.
б )
Если
)
Если![]() (рис. 73, б), то
(рис. 73, б), то![]() ,
следовательно,
,
следовательно,![]() .
.
Из пунктов а) и б) следует, что
![]() .
.
Учитывая, что ![]() ,
получаем:
,
получаем:
![]() .
.
Условие перпендикулярности двух плоскостей имеет вид:
![]() .
.
