Задания для самостоятельной работы

1. В аффинной системе координат задана прямая уравнением 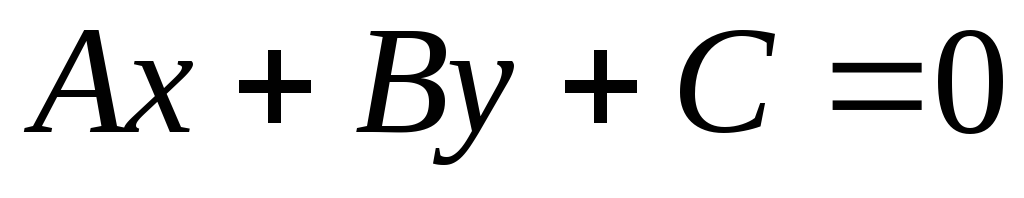. Какая фигура определяется условием: а); б)?

2. Верно ли утверждение, что прямая 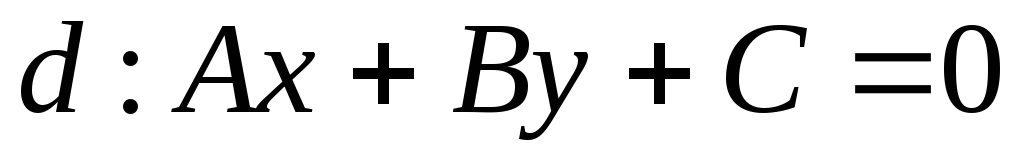пересекает отрезок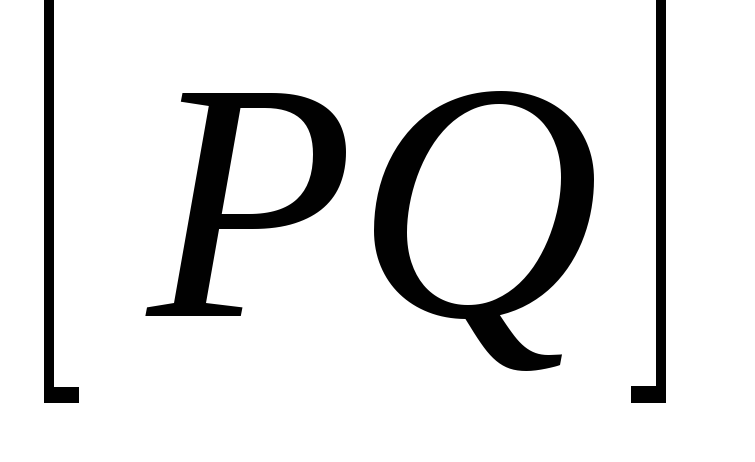, где, тогда и только тогда, когда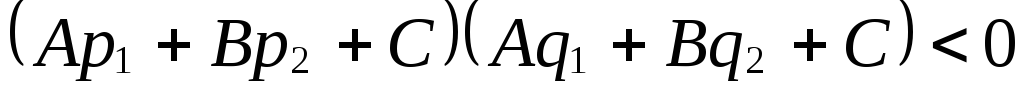и почему?

3. Даны треугольник с вершинами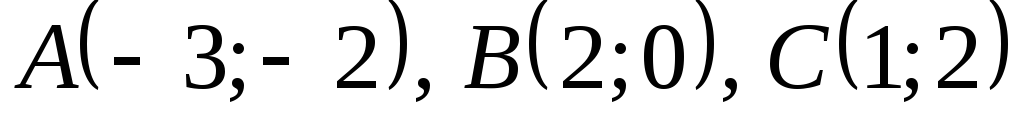и прямая. Существует ли на прямойточки, являющиеся внутренними точками треугольника?

4. Существуют ли значения коэффициентов А и В, при которых прямые, заданные уравнениям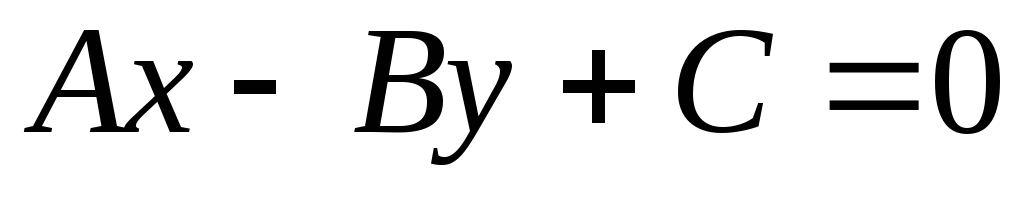и и, параллельны?

5. Какой вид имеет уравнение прямой, параллельной прямой 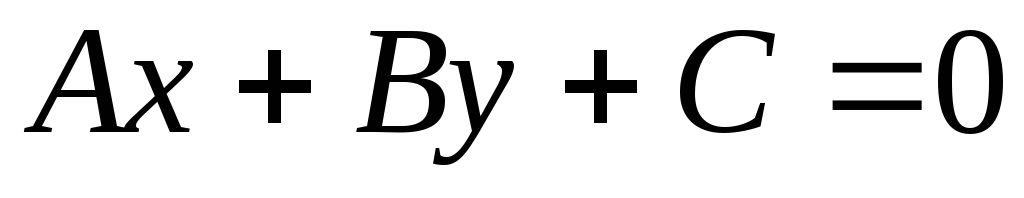и проходящей через: а) начало координат; б) точку?

6. Дано уравнение пучка прямых . Докажите, что прямыеипринадлежат этому пучку.

Лекция 10

Прямая в прямоугольной декартовой

системе координат

§18. Уравнение прямой, заданной точкой и

вектором нормали

Ненулевой вектор называется перпендикулярным данной прямой, если он ортогонален любому направляющему вектору этой прямой.

Вектор, перпендикулярный прямой, называется вектором нормали этой прямой или ее нормальным вектором. Для каждой прямой на плоскости существует бесконечное множество векторов нормали. Любые два из них коллинеарны (рис. 61).

Вектор нормали прямой будем обозначать через.

Лемма 1. Если прямая в прямоугольной системе координатзадана уравнением, то векторперпендикулярен прямой.

□ Возьмем направляющий вектор прямойи найдем скалярное произведение.■

Следствие. Уравнение прямой , заданной в прямоугольной декартовой системе координат точкойи вектором нормали, имеет вид.

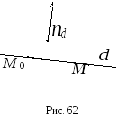
□ Если , то(рис. 62) .

Если , то векторне ортогонален вектору, т.е. .

Итак, доказано, что точка тогда и только тогда, когда ее координаты удовлетворяют уравнению

. ■ (19)

Уравнение (19) называется уравнением прямой, заданной точкой и вектором нормали.

Замечание. Если в прямоугольной декартовой системе координат прямая задана общим уравнением, то геометрический смысл коэффициентов прих и у состоит в следующем: А и В есть координаты вектора нормали прямой , т.е..

Задания для самостоятельной работы

1. Найдите координаты вектора нормали 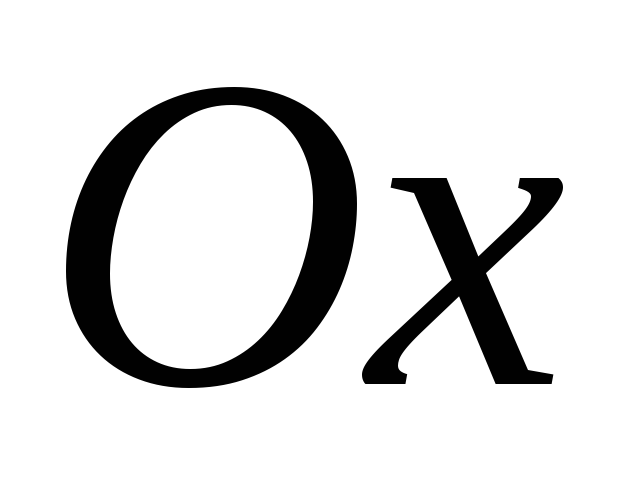оси ; оси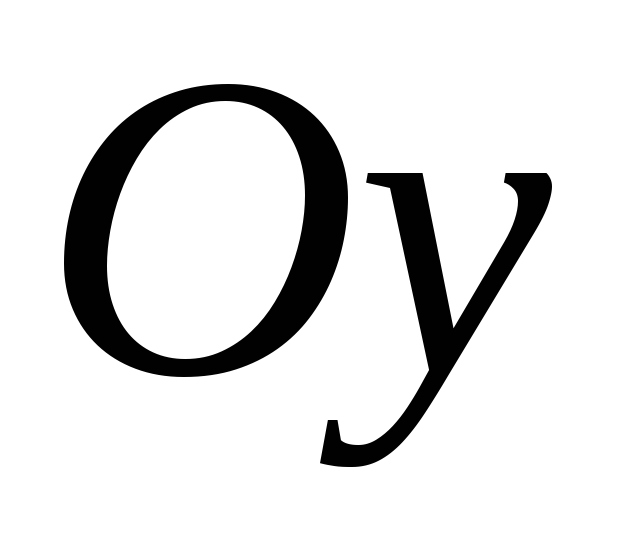прямоугольной декартовой системы координат.

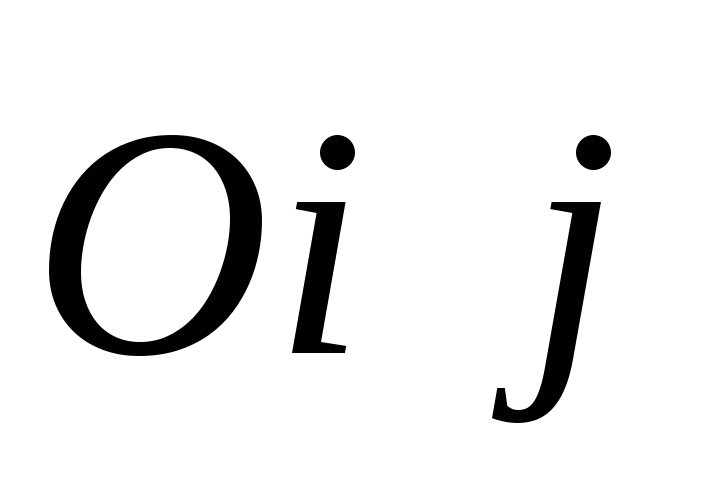2. Найдите координаты вектора нормали прямой: а) ; б); в); г).

3. Можно ли записать уравнение прямой, заданной точкой и вектором нормали, в аффинной системе координат и почему?

4. В прямоугольной декартовой системе координат прямая 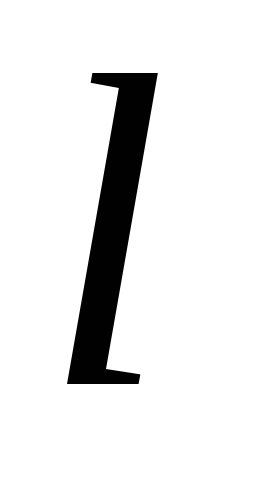задана уравнением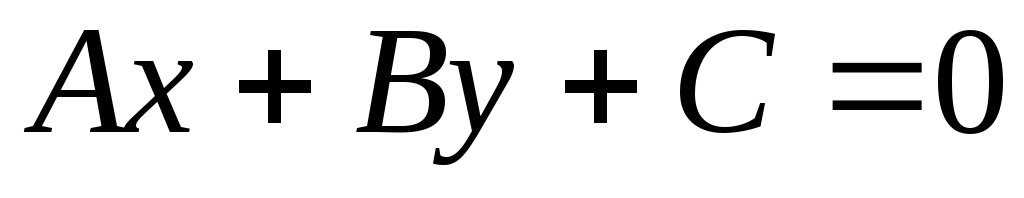. Найдите уравнение прямой, проходящей через точкуи перпендикулярной прямой. Решите задачу двумя способами.

§19. Основные метрические задачи, связанные с прямой на плоскости

1. Расстояние от точки до прямой.

Пусть на евклидовой плоскости дана прямая и точка.

Расстоянием от точки до прямой называется длина перпендикуляра , проведенного из точки к прямой (рис. 63). Если, то считают, что расстояние от до равно 0. Расстояние от точки до прямой будем обозначать через.

Поставим следующую задачу: вычислить , если известны координаты точки и общее уравнение прямой в прямоугольной декартовой системе координат. Для решения этой метрической задачи докажем теорему:

Теорема 1. Пусть в прямоугольной декартовой системе координат даны координаты точкии уравнение прямой, причем. Тогда расстояние от точки до прямой вычисляется по формуле:

.

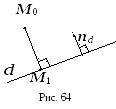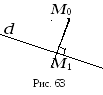
□ (рис. 64) илиили. Тогда

.

Так как , то

, т.к. . Тогда. Вычислим.

Пусть  координаты точки , тогда. Поэтому.

, откуда и получаем формулу

. ■

2. Направленный угол между двумя прямыми на ориентированной плоскости.

Две пересекающиеся прямые образуют на плоскости четыре угла. Углом между пересекающимися прямыми называется величина того из углов, который не превосходит остальные. Угол между прямыми ибудем обозначать так:. Таким образом, для любых пересекающихся прямыхи

.

На ориентированной плоскости вводится понятие направленного (ориентированного) угла между двумя прямыми.

Пусть  первая,  вторая прямая и .

Направленным углом между прямойи прямой называется направленный угол между направляющими векторами и, выбранными так, что(рис. 65).

Обратите внимание, что:

• направляющие векторы прямых иберутся не произвольно, а так, что

величина угла между ними (обычного, не направленного) не превосходит ;

• понятие направленного угла между прямыми определяется через понятие направленного угла между векторами.

Примем следующее обозначение направленного угла между прямой и прямой:. В этой записи имеет значениепорядок прямых.

Из определения направленного угла между прямыми следует, что

.

Если не перпендикулярна, то; если, тоили.

Сформулируем без доказательства следующую теорему.

Теорема 2. Если в ортонормированном базисе даны координаты любых направляющих векторовипрямыхи, не являющихся взаимно перпендикулярными, то

.

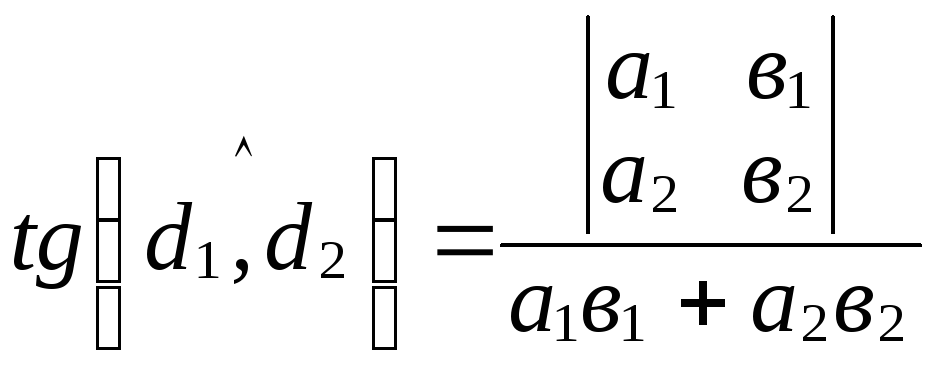Для решения задач более важными являются два следствия из этой теоремы.

Следствие 1. Пользуясь теоремой 2, выведем формулу для вычисления и условие перпендикулярности прямыхи, еслиизаданы общими уравнениями.

; .

Тогда .

а) Если не перпендикулярна, то

.

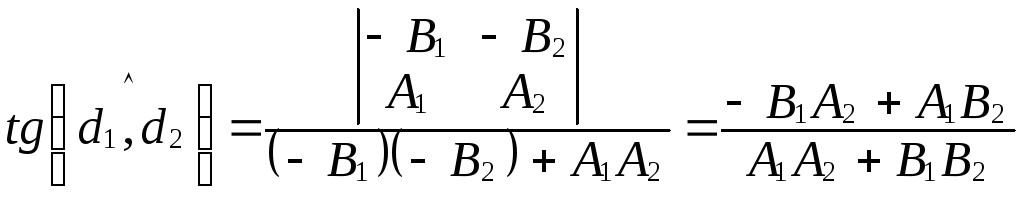Записав числитель в виде определителя, получим

.

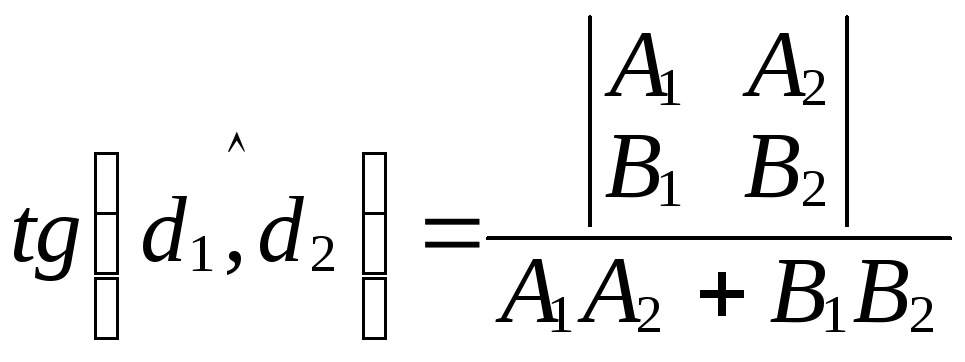б) Если , то учитывая, чтотогда и только тогда, когда, получаемусловие перпендикулярности двух прямых:

.

Следствие 2. Пусть прямые изаданы уравнениями с угловыми коэффициентами:;. Тогда(координаты направляющих векторовинаходятся после приведения уравнений прямыхик общему виду).

а) Если не перпендикулярна, то

, т.е. .

б) .

Иногда удобно пользоваться следующей записью:

.