Задания для самостоятельной работы

1. Известны координаты точки М(-2;1;0) в аффинной системе координат . Каковы координаты точки М в системе координат ?

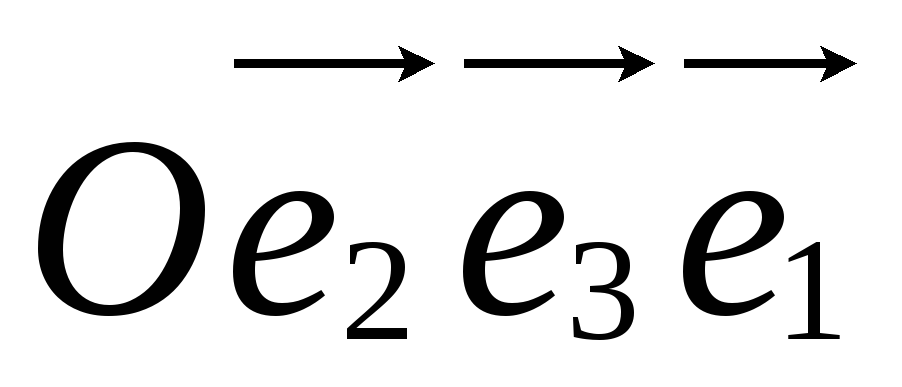2. Дано изображение аффинной системы координат 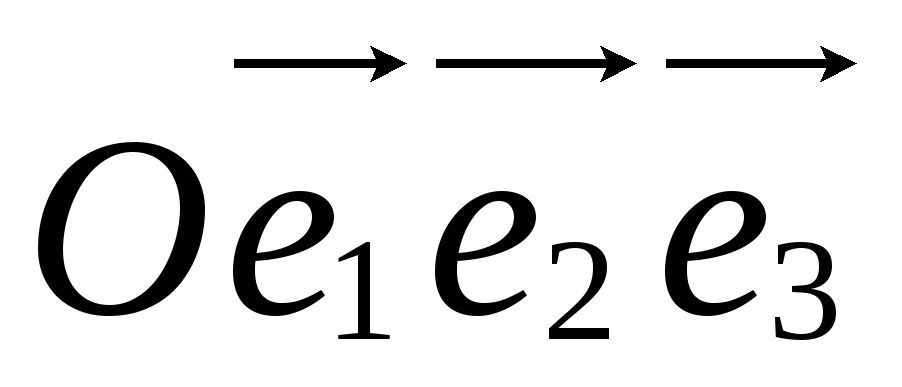. Постройте точки Р(0;-2;0), Q(0;-3;-1), N(-1;2;-4).

3. М – центр тяжести (точка пересечения медиан) треугольника АВС. Найдите координаты точки В в системе координат , не достраивая треугольникАМС до параллелограмма.

4. Докажите, пользуясь определением координат точки, что если соответственные (одноименные) координаты двух точек равны, то эти точки совпадают.

§11. Основные аффинные и метрические задачи

Задача называется метрической, если в ней фигурируют метрические свойства фигур, т.е. свойства, которые можно выявить непосредственным измерением (длина отрезка, расстояние между точками, расстояние от точки до прямой или плоскости, величина угла, перпендикулярность, площадь, объем). В аффинных задачах метрические свойства не рассматриваются. Аффинные задачи решаются в аффинной системе координат, а, следовательно, и в прямоугольной декартовой. Метрические задачи удобно решать в прямоугольной системе координат.

Основные аффинные и метрические задачи, решаемые с помощью координат, сформулируем в виде теорем.

Основные аффинные задачи

1. Координаты вектора, заданного двумя точками.

Теорема 1. Если в аффинной системе координат и, то.

Представим векторв виде разности векторови:

.

Так как, то по определению координат точки. Аналогично. Применяя свойство координат векторов (координаты разности двух векторов равны разности их соответствующих координат), получаем, что векторимеет координаты .

2. Деление отрезка в данном отношении.

Говорят, что точка М делит направленный отрезок в отношении , если выполняется векторное равенство:

. (1)

Число при этом называется простым отношением трех точек М₁, М₂ и М. Простое отношение трех точек М₁, М₂ и М обозначается так: .

Почему в определении деления отрезка в данном отношении ?

Пусть М₁М₂ и точка М делит направленный отрезок в отношении =-1. Тогда по определению деления отрезка в данном отношении

,

т.е.   . А так как начало у векторовиобщее и они равны, тоМ₁=М₂. Получили противоречие с условием, следовательно, .

Из векторного равенства (1) следует, что если , то, т.е. точкаМ совпадает с точкой М₁; если >0, то точка М лежит внутри отрезка (рис. 37), т.е.; если<0, то точка М лежит на прямой вне отрезка(рис. 38), т.е.или.

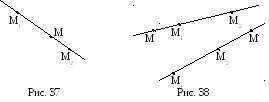
Теорема 2. Пусть в аффинной системе координат ,. Тогда координаты точки, делящей направленный отрезокв отношении, находятся по формулам:

; ;. (2)

По определению деления отрезка в данном отношении .

По теореме 1,. Тогда. Так как два вектора равны тогда и только тогда, когда равны их соответствующие координаты, то;;

, откуда получаем: ;;.

Формулы (2) называются формулами деления отрезка в данном отношении в координатах.

Из теоремы 2 получаем

Следствие. Если М(х;у;z) – середина отрезка М₁М₂ с концами и, то,,.

Так как М – середина М₁М₂, то  =1. Применяя формулы деления отрезка в данном отношении в координатах, получаем:

, ,.