Задания для самостоятельной работы

1. Дано общее уравнение 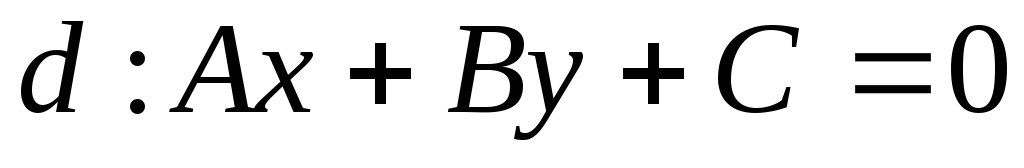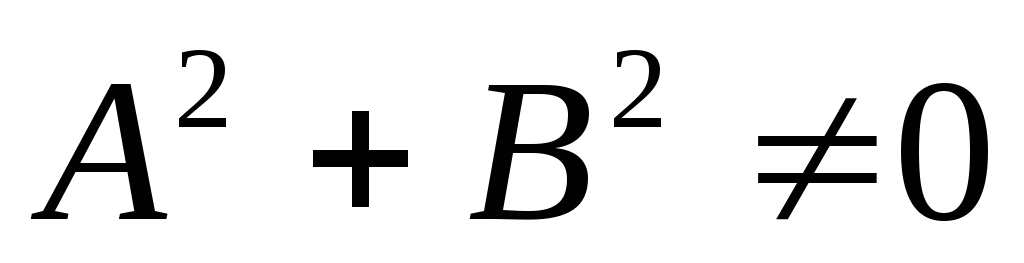прямой ,. Получите из него для прямойканоническое, параметрическое уравнения, уравнение с угловым коэффициентом и уравнение «в отрезках».

2. Дано параметрическое уравнение прямой :

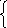
Получите из них общее уравнение прямой .

3. Найдите двумя способами (пользуясь частным случаем общего уравнения прямой и пользуясь различными уравнениями прямой) уравнение прямой, проходящей:

а) через точку параллельно оси;

б) через точку параллельно оси;

в) через начало координат и точку .

4. Выведите условие параллельности вектора 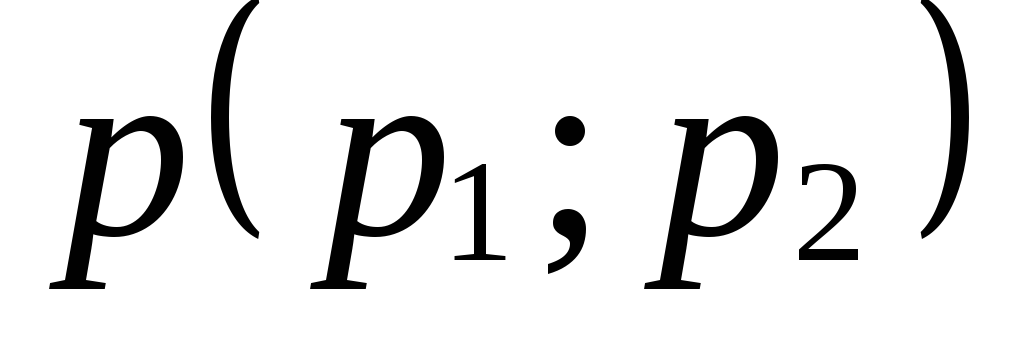и прямой, заданной в аффинной системе координат общим уравнением.

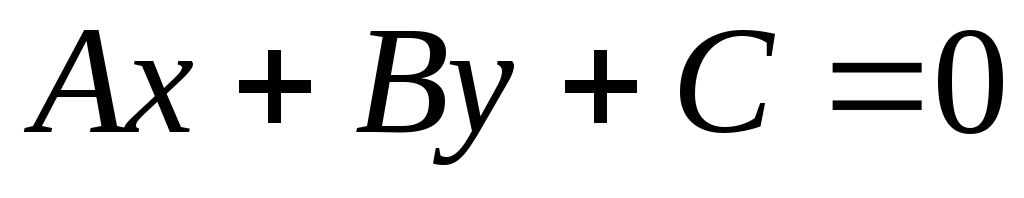5. Прямая задана в прямоугольной системе координат общим уравнением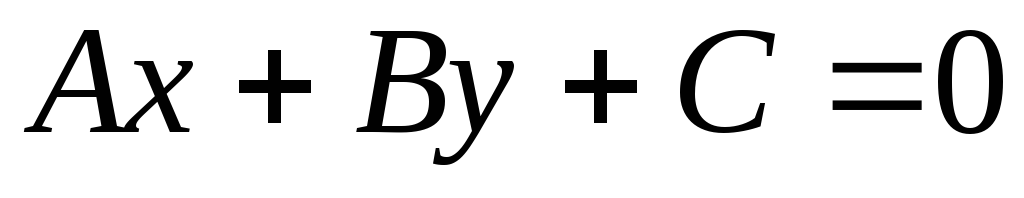. Выведите условие перпендикулярности вектора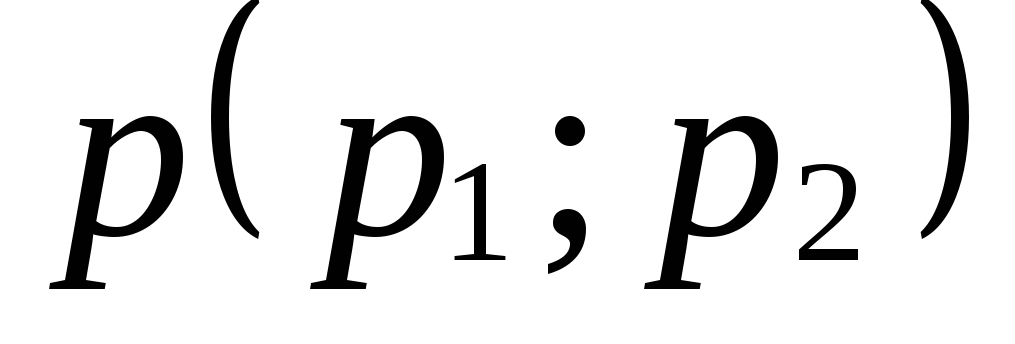и прямой.

§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)

1. Геометрический смысл знака трехчлена .

Теорема 1. Если в аффинной системе координат прямая задана уравнением, то полуплоскости с границейопределяются неравенствамии.

Сформулированная теорема, выражающая геометрический смысл знака трехчлена , позволяет выяснять, лежат ли две точки по одну сторону от прямойили по разные стороны. Рассмотрим простейший пример.

Задача 1. Выяснить, пересекает ли прямая отрезок, если.

Решение. Определим знак трехчлена в точке.

Определим знак трехчлена в точке.

Следовательно, точки илежат по разные стороны от данной прямой, поэтому прямаяпересекает отрезок.

Выяснение расположения точек относительно прямой, в свою очередь, применяется при решении геометрических задач, связанных с нахождением условий, определяющих внутренние области углов, треугольников или полос.

2. Взаимное расположение двух прямых.

Теорема 2. Пусть в аффинной системе координат прямая задана уравнением уравнением .

1) Прямые ипересекаются тогда и только тогда, когда коэффициенты приив их уравнениях не пропорциональны, т.е.

;

Чтобы найти координаты точки пересечения прямыхи, надо решить систему уравненийи.

2) Прямые ипараллельны тогда и только тогда, когда коэффициенты приипропорциональны, а свободные члены им не пропорциональны, т.е.

;

3) Прямые исовпадают тогда и только тогда, когда коэффициенты приии свободные члены в их уравнениях пропорциональны, т.е.

.

Рассмотрим пример применения этой теоремы.

Задача 2. Выяснить взаимное расположение прямых и.

Решение. Находим из уравнений прямых .

Отношение мы найти не можем, т.к. делить на 0 нельзя. Поэтому поменяем прямые местами и найдем отношения

.

Следовательно, прямые ипересекаются. Отношениенаходить уже нет необходимости.

Задача 3. Найти уравнение прямой, проходящей через точку и параллельной прямой.

Решение. Пусть  искомая прямая.

Заметим, что задачу можно решить разными способами. Например, взяв за направляющий вектор прямой направляющий векторпрямой(т.к., то), можно воспользоваться каноническим уравнением прямой.

Но мы решим задачу, используя теорему 2.

Из теоремы 2 следует, что так как , то общее уравнение прямойбудет иметь вид:

,

т.е. можно считать, что отличаться уравнения прямых ибудут только свободными членами.

Чтобы найти С, используем то, что . Подставляя координаты точкив уравнение прямой, найдемС: .

Тогда

.

3. Пучок прямых. Уравнение пучка прямых.

Множество всех прямых плоскости, проходящих через данную точку , называетсяпучком прямых. Точка называетсяцентром этого пучка.

Множество всех прямых плоскости, параллельных данной прямой , называетсяпучком параллельных прямых.

Пучок прямых определяется заданием его центра , пучок параллельных прямых – заданием ненулевого вектора, параллельного прямым пучка.

Теорема 3. Пусть известны в аффинной системе координат уравнения двух прямых пучка с центром в точке :

,

.

Тогда уравнение пучка прямых с центром будет иметь вид:

,

где действительные числа, не равные нулю одновременно. Они определяют некоторую прямую пучка.

Геометрический смысл и: это координаты направляющего векторапрямойв базисе(рис. 60).

Рассмотрим пример применения этой теоремы.

Задача 4. Найти уравнение прямой , проходящей через точкуи через точку пересечения прямыхи.

Решение. Заметим, что искомое уравнение можно найти, вычислив координаты точки пересечения прямыхии применив уравнение прямой, заданной двумя точками. Но при решении системы уравнений прямыхиполучаются громоздкие вычисления.

Поэтому задачу лучше решить по теореме 3. Запишем уравнение пучка прямых с центром в точке :

, (18)

где .

Так как , то искомая прямая принадлежит данному пучку. Найдеми, определяющие. Так как, то ее координаты удовлетворяют уравнению (18):

. Подставим в уравнение (18):. Заметим, что(действительно, если, то противоречие с условием ).

Разделим обе части уравнения на :

; .