
- •Кафедра алгебры, геометрии, теории и методики обучения математике
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •Свойства умножения вектора на число
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •Применение векторного произведения
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •Лекция 10
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§ 22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости
- •Задания для самостоятельной работы
- •§ 23. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§ 24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§ 25. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§ 26. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§ 27. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
§21. Общее уравнение плоскости
Теорема 1.
Плоскость есть поверхность первого
порядка, т.е. задается в аффинной системе
координат уравнением первой степени
![]() ,
где
,
где![]() не равны нулю одновременно. Обратно,
поверхность в пространстве, заданная
в аффинной системе координат уравнением
первой степени
не равны нулю одновременно. Обратно,
поверхность в пространстве, заданная
в аффинной системе координат уравнением
первой степени![]() (где
(где![]() не равны нулю одновременно), есть
плоскость.
не равны нулю одновременно), есть
плоскость.
□ Пусть плоскость
![]() задана точкой
задана точкой![]() и двумя неколлинеарными векторами
и двумя неколлинеарными векторами![]() и
и![]() ,
т.е.
,
т.е.
![]() .
Найдем ее уравнение.
.
Найдем ее уравнение.
 ;
;
![]() ;
;
 .
.
Положим ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
Так как векторы
![]() и
и![]() неколлинеарны, то их соответствующие
координаты не пропорциональны,
следовательно,
неколлинеарны, то их соответствующие
координаты не пропорциональны,
следовательно,![]() ,
,
![]() и
и ![]() одновременно, т.е.
одновременно, т.е.
![]() одновременно.
одновременно.
Докажем обратное
утверждение. Пусть некоторая поверхность
![]() задана уравнением
задана уравнением![]() ,
где
,
где![]() не равны нулю одновременно. Докажем,
что
не равны нулю одновременно. Докажем,
что![]()
плоскость.
плоскость.
Пусть для
определенности
![]() .
Найдем уравнение плоскости
.
Найдем уравнение плоскости![]() ,
заданной точкой
,
заданной точкой![]() и двумя неколлинеарными векторами
и двумя неколлинеарными векторами![]() и
и![]() .
.
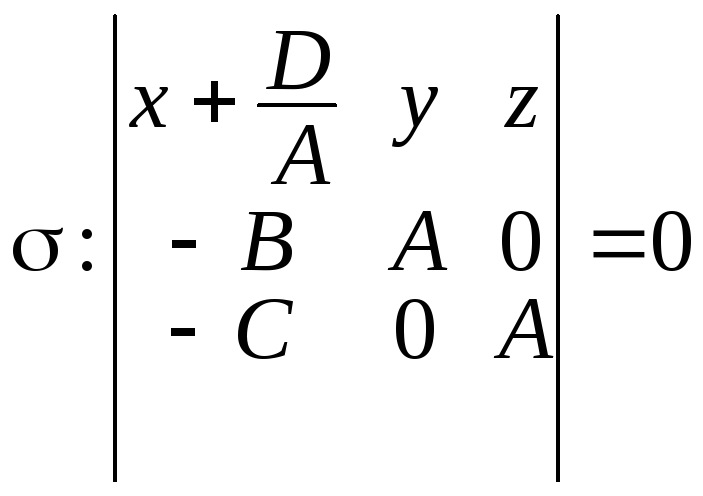 ;
;
![]() ;
;
![]() ;
разделив обе части полученного уравнения
на
;
разделив обе части полученного уравнения
на![]() ,
получим:
,
получим:
![]() .
.
Итак, уравнение
поверхности
![]() в точности совпадает с уравнением
плоскости
в точности совпадает с уравнением
плоскости![]() ,
следовательно,
,
следовательно,![]() совпадает с
совпадает с![]() ,
т.е.
,
т.е.![]()
плоскость.
плоскость.
Если
![]() ,
то
,
то![]() или
или![]() .
Аналогичными рассуждениями убеждаемся,
что
.
Аналогичными рассуждениями убеждаемся,
что![]()
плоскость. ■
плоскость. ■
Уравнение
![]() (где
(где![]() не равны нулю одновременно) называетсяобщим
уравнением плоскости.
Переменные х,
у,
z
называются текущими
координатами произвольной точки
плоскости.
не равны нулю одновременно) называетсяобщим
уравнением плоскости.
Переменные х,
у,
z
называются текущими
координатами произвольной точки
плоскости.
Задания для самостоятельной работы
Можно ли пользоваться общим уравнением плоскости в прямоугольной декартовой системе координат и почему?
Выведите в аффинной системе координат уравнение

 плоскости, проходящей через точку
плоскости, проходящей через точку .
.Дано общее уравнение плоскости
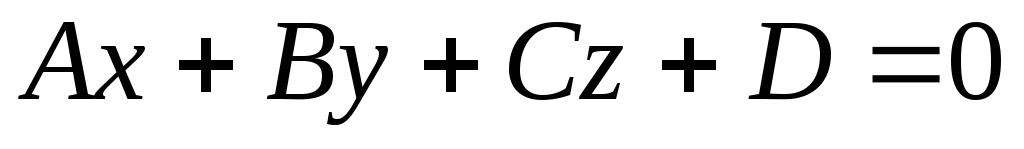 ,
в котором все коэффициенты прих,
у
и z
и свободный член отличны от нуля.
Получите из него уравнение плоскости
«в отрезках».
,
в котором все коэффициенты прих,
у
и z
и свободный член отличны от нуля.
Получите из него уравнение плоскости
«в отрезках».Дано параметрическое уравнение плоскости. Получите из него общее уравнение плоскости.
Дано общее уравнение плоскости. Получите из него параметрическое уравнение плоскости.
Какая поверхность в пространстве задается в аффинной системе координат уравнением: а)
 ;
б)
;
б)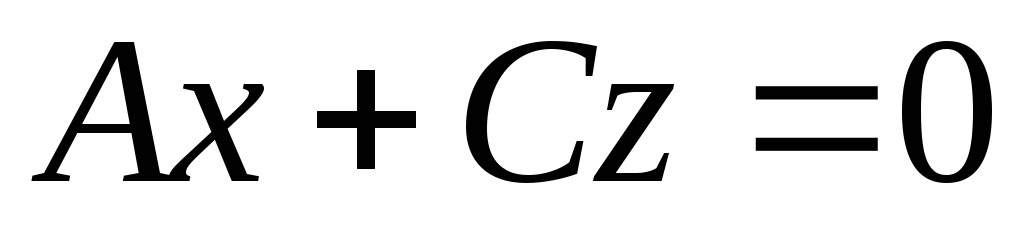 ;
в)
;
в)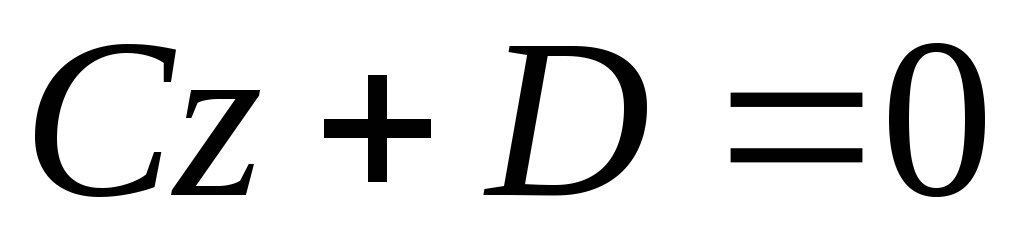 ;
г)
;
г)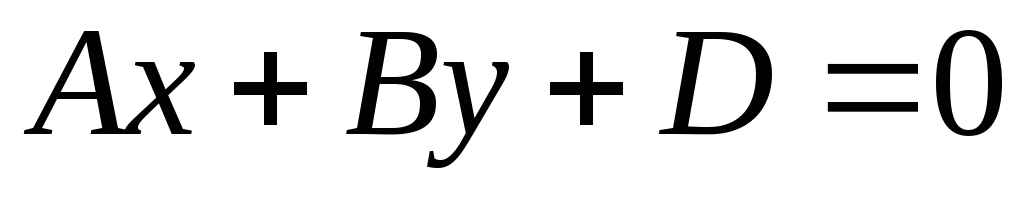 ;
д)
;
д)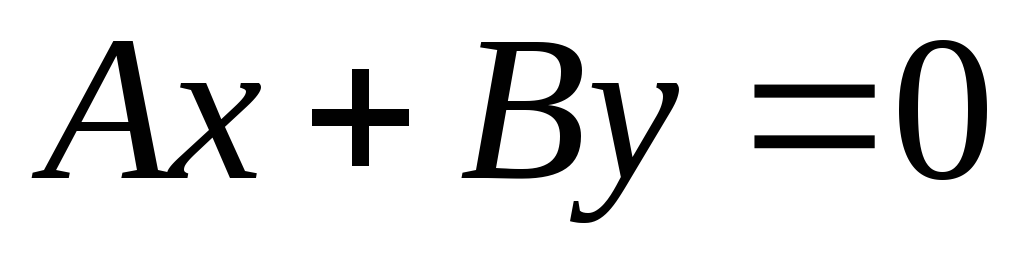 ?
?
§ 22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости
Лемма 1 (о
параллельности вектора и плоскости).
Пусть в аффинной системе координат
![]() дана плоскость
дана плоскость![]() и вектор
и вектор![]() .
Для того, чтобы вектор
.
Для того, чтобы вектор![]() был параллелен плоскости
был параллелен плоскости![]() ,
необходимо и достаточно, чтобы выполнялось
условие
,
необходимо и достаточно, чтобы выполнялось
условие![]() .
.
□ Чтобы доказать
необходимость и достаточность этого
условия, возьмем точку
![]() и отложим от нее вектор
и отложим от нее вектор![]() (рис. 69).
(рис. 69).
Пусть
![]() ,
тогда
,
тогда![]() .
.
И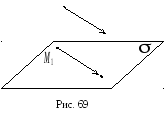 з
равенства векторов
з
равенства векторов![]() и
и![]() следует равенство
их соответственных координат:
следует равенство
их соответственных координат:
![]() .
(24)
.
(24)
Так как
![]() ,
то
,
то
![]() .
(25)
.
(25)
Если
![]() ,
то
,
то![]() ,
следовательно,
,
следовательно,
![]() .
(26)
.
(26)
Вычитаем почленно из уравнения (26) уравнение (25):
![]() .
.
Применяя формулы (24), получаем:
![]() .
.
Обратно, пусть
имеет место условие
![]() .
Тогда из формул (24) следует, что
.
Тогда из формул (24) следует, что![]() .
.
Сложив почленно последнее уравнение с уравнением (25), получим:
![]() ,
,
откуда следует,
что
![]() .
Поэтому
.
Поэтому![]() ,
а так как
,
а так как![]() ,
то
,
то![]() .■
.■
Выясним особенности
расположения плоскости
![]() относительно аффинной системы координат,
если некоторые из коэффициентов в ее
общем уравнении равны 0.
относительно аффинной системы координат,
если некоторые из коэффициентов в ее
общем уравнении равны 0.
1.
![]()
верное равенство
верное равенство
![]() .
.
Обратно, пусть
![]() ,
тогда
,
тогда![]()
верное равенство
верное равенство
![]() .
.
Итак,
![]() .
.
2.
![]() .
.
Возьмем вектор
![]() .
Проверим выполнимость условия
.
Проверим выполнимость условия![]() :
:
![]() ;
;
0=0.
Следовательно, по
лемме о параллельности вектора и
плоскости
![]() .
Поэтому возможны два случая
.
Поэтому возможны два случая![]() или
или![]() .
Учитывая, что
.
Учитывая, что![]() ,
т.е.
,
т.е.![]() ,
получаем:
,
получаем:![]() .
.
Обратно, пусть
![]() ,
тогда
,
тогда![]() .
По лемме о параллельности вектора и
плоскости
.
По лемме о параллельности вектора и
плоскости![]() .
.
Итак,
![]() .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 3 и 4 :
3.
![]() .
.
4.
![]() .
.
5. Пусть
![]() и
и![]() .
Тогда из пункта 2 следует, что
.
Тогда из пункта 2 следует, что![]() ,
т.е.
,
т.е.![]() или
или![]() ;
а из пункта 1 следует, что
;
а из пункта 1 следует, что![]() .
Значит,
.
Значит,![]() .
.
Обратно, пусть
![]() .
Тогда
.
Тогда![]() ,
т.е.
,
т.е.![]() (см. пункт 1). Кроме того,
(см. пункт 1). Кроме того,![]() (см. пункт 2).
(см. пункт 2).
Итак,
![]() и
и![]() .
.
В этом случае
уравнение плоскости
![]() примет вид
примет вид![]() .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 6 и 7:
6.
![]() и
и![]() .
.
7.
![]() и
и![]() .
.
8.
![]() и
и![]() .
Тогда из пункта 2 следует, что
.
Тогда из пункта 2 следует, что![]() ;
а из пункта 3 следует, что
;
а из пункта 3 следует, что![]() .
Таким образом,
.
Таким образом,
![]() и
и
![]() .
.
В этом случае
уравнение
![]() примет вид
примет вид![]() или
или![]() (где
(где![]() ).
).
Рассуждая аналогично, рассмотрите случаи 9 и 10:
9.
![]() и
и![]() .
.
10.
![]() и
и![]() .
.
Из пунктов 8 и 1 получаем случай
11.
![]() ,
,![]() и
и![]() .
.
В этом случае
уравнение плоскости будет иметь вид
![]() ,
т.е.
,
т.е.
![]() .
.
Из пунктов 9 и 1 получаем случай
12.
![]() ,
,![]() и
и![]() .
.
Тогда уравнение
![]() будет иметь вид
будет иметь вид![]() ,
т.е.
,
т.е.
![]() .
.
Из пунктов 10 и 1 получаем случай
13.
![]() ,
,![]() и
и![]() .
.
Уравнение
![]() в этом случае имеет вид
в этом случае имеет вид![]() ,
т.е.
,
т.е.
![]() .
.
