
- •Кафедра алгебры, геометрии, теории и методики обучения математике
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •Свойства умножения вектора на число
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •Применение векторного произведения
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •Лекция 10
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§ 22. Лемма о параллельности вектора и плоскости. Частные случаи общего уравнения плоскости
- •Задания для самостоятельной работы
- •§ 23. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§ 24. Плоскость в прямоугольной системе координат. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§ 25. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§ 26. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§ 27. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
Задания для самостоятельной работы
Найдите каноническое уравнение оси
 ;
оси
;
оси аффинной системы координат
аффинной системы координат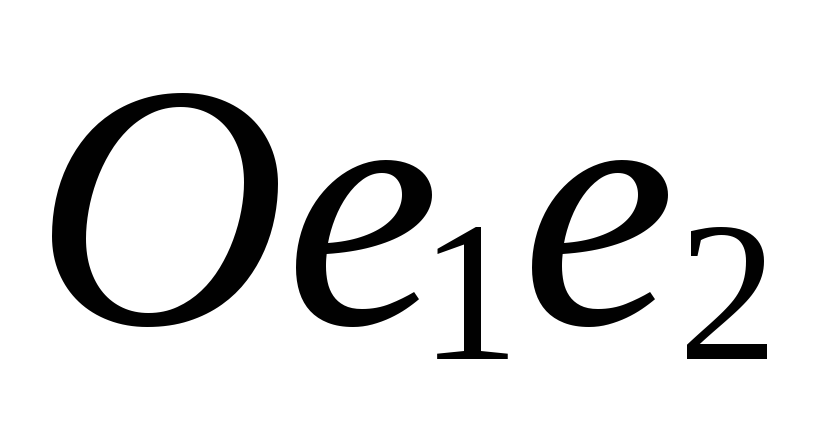 .
.Найдите каноническое уравнение прямой, отсекающей на координатных осях отрезки
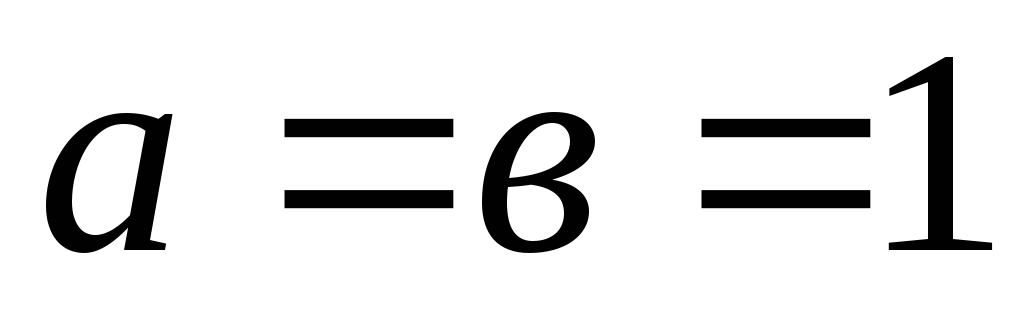 .
.Могут ли числа а и в в уравнении прямой «в отрезках» быть равными нулю одновременно? Почему? Может ли только одно из чисел равняться 0? Почему?
Какое из следующих шести уравнений является уравнением прямой в «в отрезках», а какое – не является и почему? Как привести его к виду «в отрезках»?
|
а)
|
г)
|
ж)
|
|
б)
|
д)
|
з)
|
|
в)
|
е)
|
и)
|
Напишите уравнение прямой, отсекающей на оси ординат отрезок
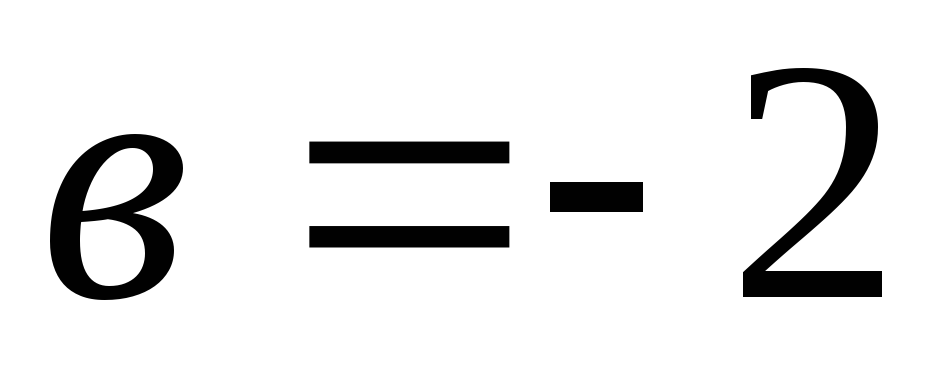 и имеющей угловой коэффициент
и имеющей угловой коэффициент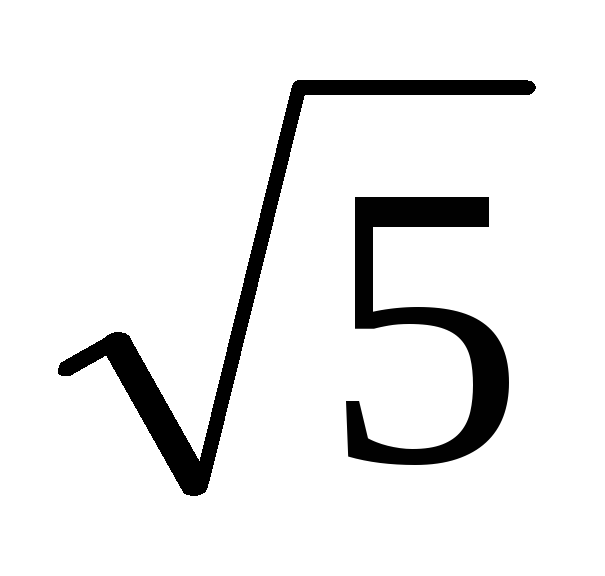 .
.Почему для прямой, параллельной оси
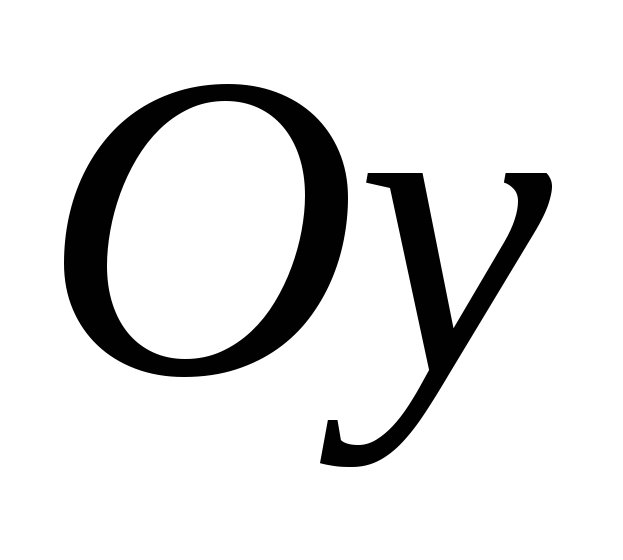 ,
не существует уравнения с угловым
коэффициентом? Существует ли для такой
прямой уравнение прямой, заданной
точкой и угловым коэффициентом и почему?
,
не существует уравнения с угловым
коэффициентом? Существует ли для такой
прямой уравнение прямой, заданной
точкой и угловым коэффициентом и почему?Напишите уравнение прямой, проходящей через точку
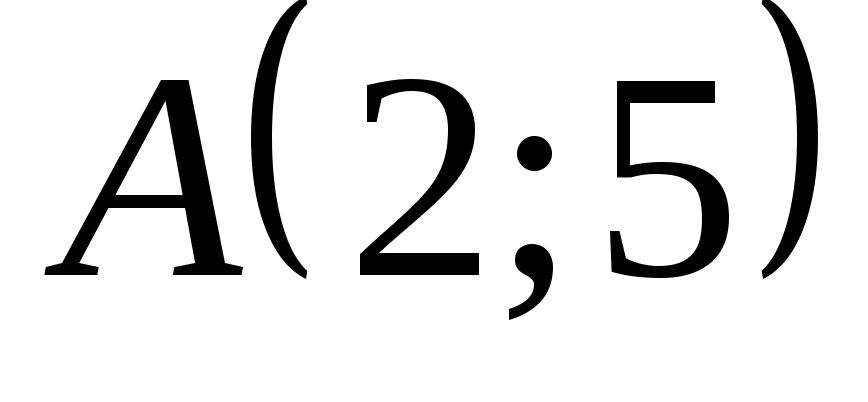 и не имеющей углового коэффициента.
и не имеющей углового коэффициента.Напишите уравнения всех прямых, содержащих стороны правильного шестиугольника
 ,
если сторона шестиугольника равнаа,
а система координат
,
если сторона шестиугольника равнаа,
а система координат
 выбрана так, что началоО
совпадает с точкой А,
точка В
лежит на положительном луче оси
выбрана так, что началоО
совпадает с точкой А,
точка В
лежит на положительном луче оси
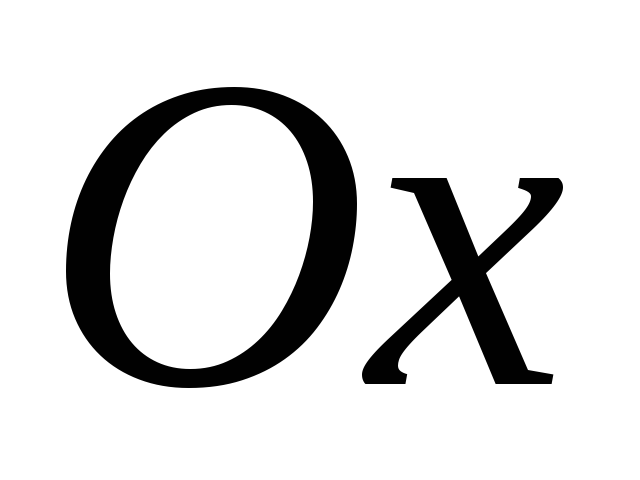 и точкаЕ –
на положительном луче оси
и точкаЕ –
на положительном луче оси
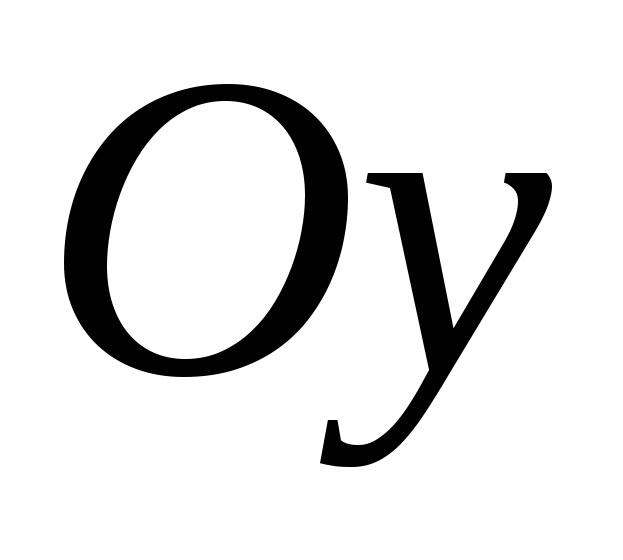 .
.Напишите уравнение прямой, которая проходит через точку
 и отсекает от координатного угла
треугольник с площадью, равной 12. Система
координат прямоугольная декартова.
и отсекает от координатного угла
треугольник с площадью, равной 12. Система
координат прямоугольная декартова.Можно ли пользоваться уравнениями (10)-(17) в прямоугольной декартовой системе координат на плоскости и почему?
§16. Общее уравнение прямой и его частные случаи
Докажем следующую теорему об общем уравнении прямой:
Теорема 1.
Любая прямая на плоскости задается в
аффинной системе координат уравнением
первой степени с двумя неизвестными
![]() ,
гдеА
и В
не равны 0 одновременно. Обратно, линия
на плоскости, заданная в аффинной системе
координат уравнением первой степени
,
гдеА
и В
не равны 0 одновременно. Обратно, линия
на плоскости, заданная в аффинной системе
координат уравнением первой степени
![]() (гдеА
и В
не равны 0 одновременно), есть прямая.
Вектор
(гдеА
и В
не равны 0 одновременно), есть прямая.
Вектор
![]() является направляющим вектором этой
прямой.
является направляющим вектором этой
прямой.
□ Пусть
![]()
прямая,
прямая,
![]() .
Запишем каноническое уравнение прямой
.
Запишем каноническое уравнение прямой![]() :
:
![]() .
.
Преобразуем его:
![]()
![]()
![]() .
.
Положим
![]() .
Тогда уравнение прямой
.
Тогда уравнение прямой![]() имеет вид:
имеет вид:
![]() .
.
Так как
![]() (по определению), то
(по определению), то![]() и
и![]() не равны 0 одновременно, следовательно,А
и В
не равны 0 одновременно.
не равны 0 одновременно, следовательно,А
и В
не равны 0 одновременно.
Докажем обратное
утверждение. Пусть некоторая линия
![]() задана в аффинной системе координат на
плоскости уравнением
задана в аффинной системе координат на
плоскости уравнением![]() ,
где
,
где![]() .
Докажем, что
.
Докажем, что![]()
прямая.
прямая.
Найдем уравнение
прямой
![]() ,
заданной точкой
,
заданной точкой![]() и направляющим вектором
и направляющим вектором![]() ,
гдеА,
В
и С
взяты из уравнения линии
,
гдеА,
В
и С
взяты из уравнения линии
![]() :
:
 .
.
Преобразуем это
уравнение:
![]() .
Итак,
.
Итак,![]() ,
причем
,
причем![]() ,
т.к.
,
т.к.![]() .
.
Уравнение прямой
![]() в точности совпадает с уравнением линии
в точности совпадает с уравнением линии![]() ,
следовательно,
,
следовательно,![]() совпадает с
совпадает с![]() ,
т.е.
,
т.е.![]() есть прямая.
есть прямая.
Так как вектор
![]() является направляющим вектором прямой
является направляющим вектором прямой![]() ,
а
,
а![]() совпадает с
совпадает с![]() ,
то
,
то![]()
направляющий вектор прямой
направляющий вектор прямой
![]() .■
.■
Уравнение
![]() называетсяобщим
уравнением прямой;
называетсяобщим
уравнением прямой;
х и у – текущие координаты произвольной точки прямой.
Частные случаи общего уравнения прямой
Выясним особенности
расположения прямой
![]() относительно аффинной системы координат
относительно аффинной системы координат![]() ,
если некоторые из чиселА,
В
и С
равны нулю.
,
если некоторые из чиселА,
В
и С
равны нулю.
Пусть С=0. Тогда уравнение прямой
 примет вид:
примет вид: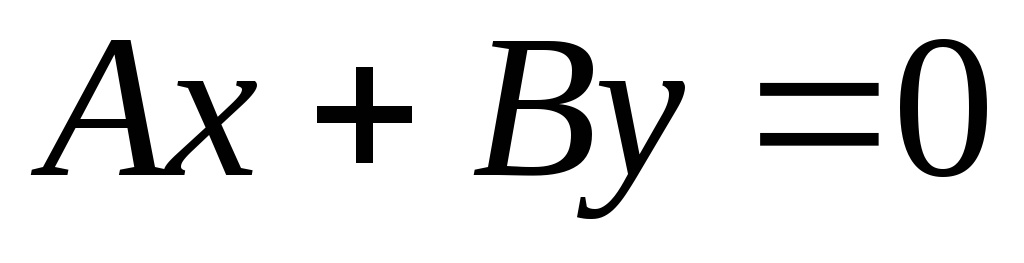 .
Подставляя координаты точки
.
Подставляя координаты точки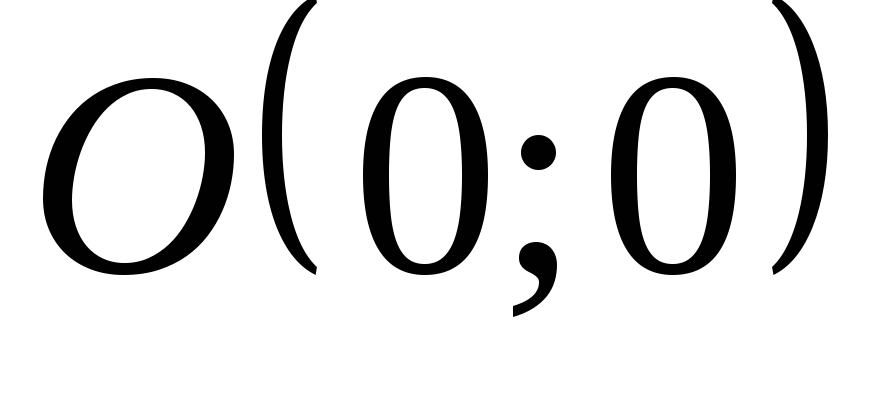 в это уравнение, убеждаемся, что
получается верное равенство
в это уравнение, убеждаемся, что
получается верное равенство
![]() ,
,
следовательно,
![]() ,
т.е. прямая
,
т.е. прямая![]() проходит через начало координат.
проходит через начало координат.
Обратно, пусть
![]() .
Тогда
.
Тогда![]() .
.
Итак,
![]() .
.
2) Пусть
![]() .
Тогда
.
Тогда![]() .
Учитывая, что
.
Учитывая, что![]() ,
получаем, что
,
получаем, что![]() .
.
Обратно, если
![]() ,
то
,
то![]() .
.
Итак,
![]() .
.
При этом уравнение
![]() имеет вид
имеет вид![]() или
или![]() (где
(где![]() ).
).
3) Утверждение «![]() »
предлагаем читателю доказать
самостоятельно.
»
предлагаем читателю доказать
самостоятельно.
Из пунктов 1) и 2) следует пункт
4) А=0
и С=0![]() совпадает с осью
совпадает с осью![]() .
В этом случае прямая
.
В этом случае прямая![]() (т.е. ось
(т.е. ось![]() )
задается уравнением
)
задается уравнением![]() .
.
Из пунктов 1) и 3) следует пункт
5) В=0
и С=0![]() совпадает с осью
совпадает с осью![]() .
В этом случае прямая
.
В этом случае прямая![]() (т.е. ось
(т.е. ось![]() )
задается уравнением
)
задается уравнением![]() .
.

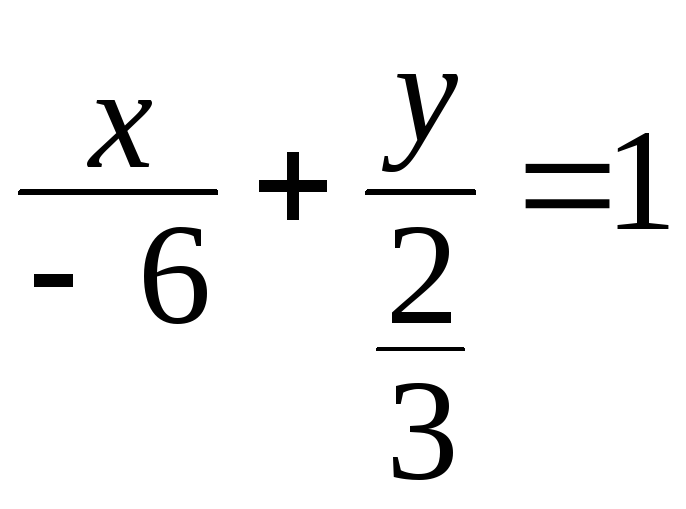 ;
; ;
;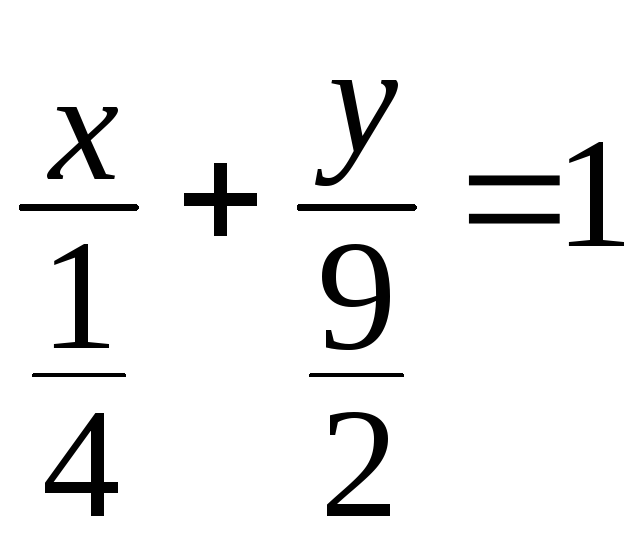 ;
;