Задания для самостоятельной работы

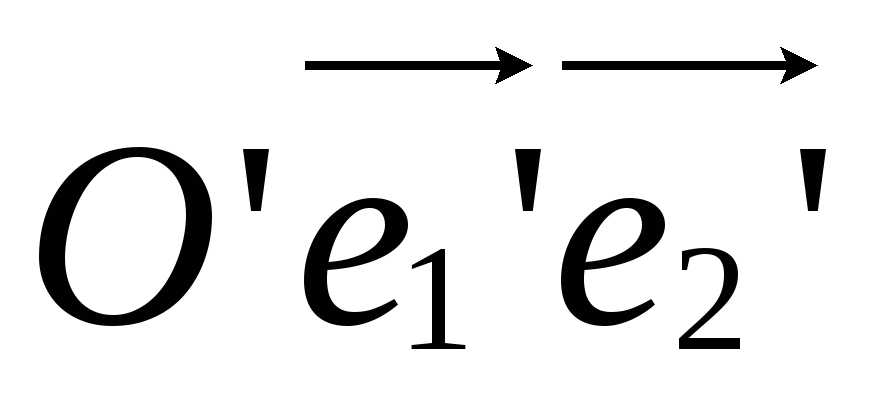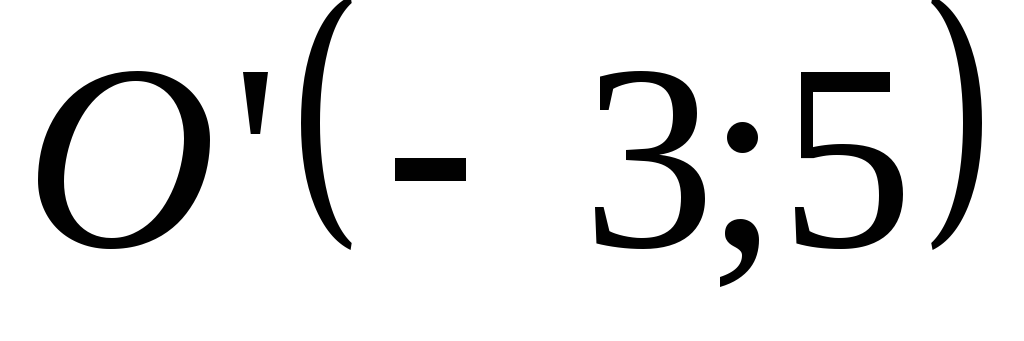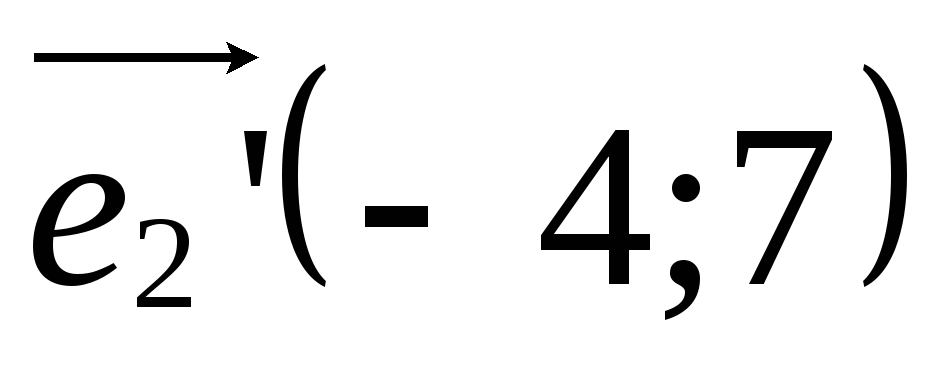1. Напишите формулы преобразования аффинной системы координат в аффинную систему координат, если,,в системе.

2. Может ли матрица перехода от базиса 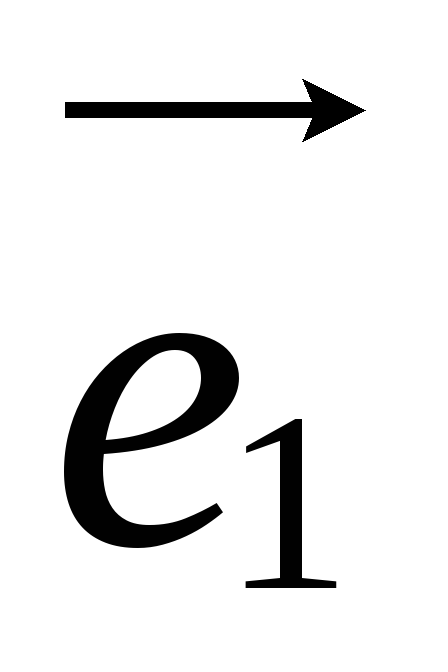,к базису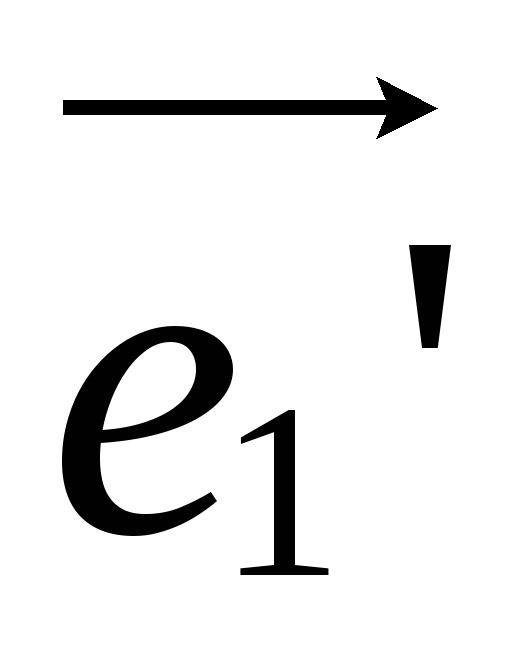,иметь вид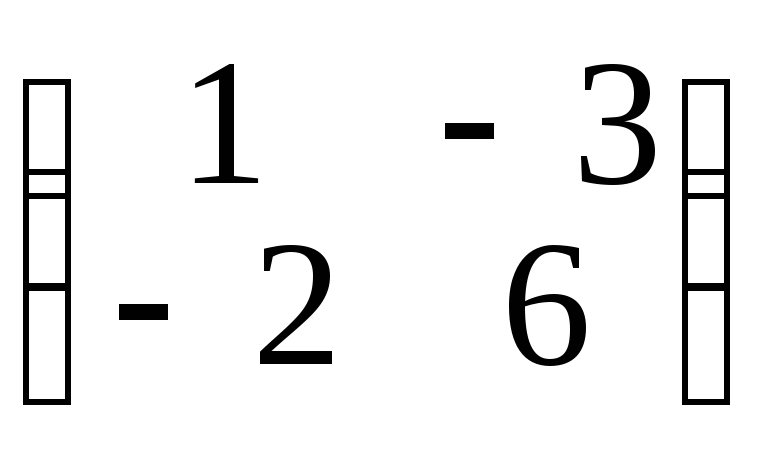и почему?

3. Напишите формулы переноса начала, если в системе координат.

4. Напишите формулы замены координатных векторов, если ,.

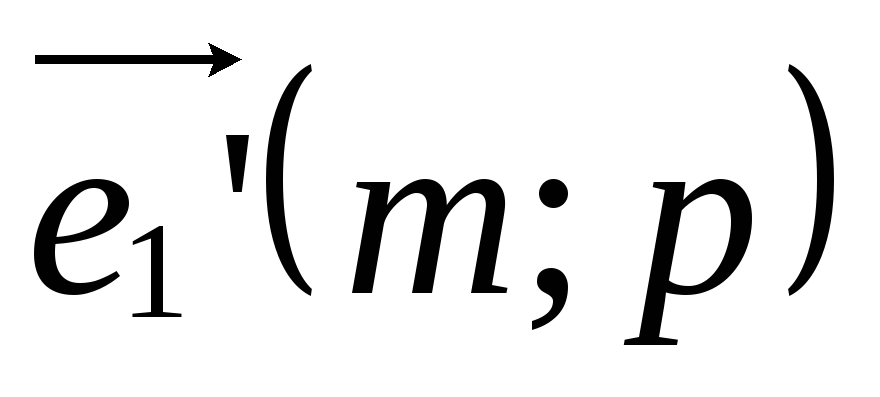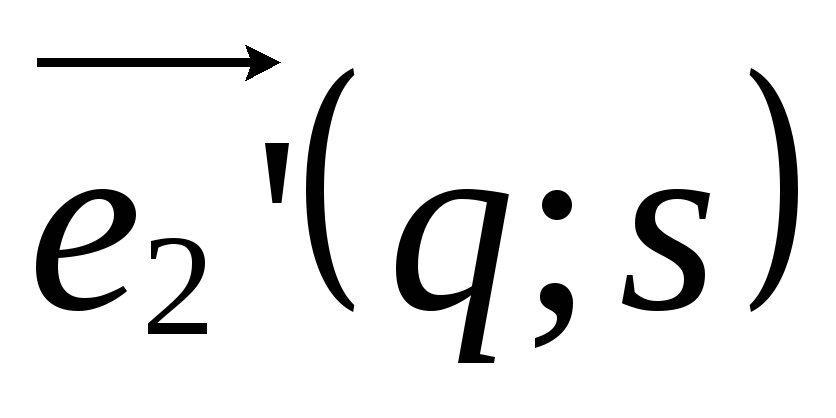5. Запишите матрицу перехода от базиса 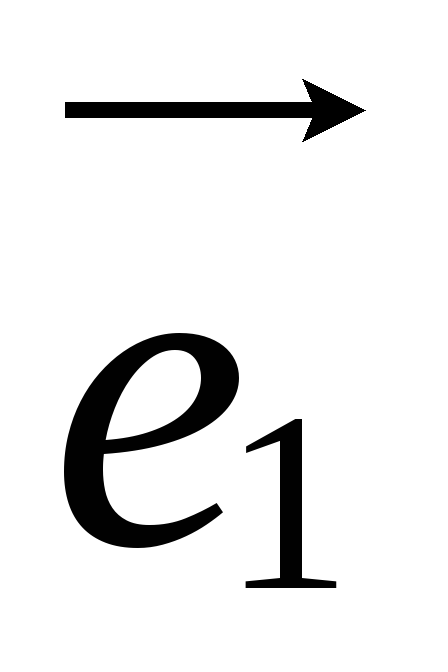,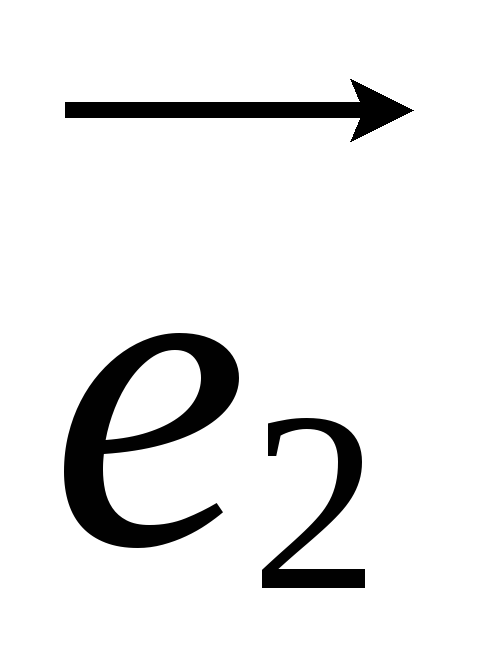к базису,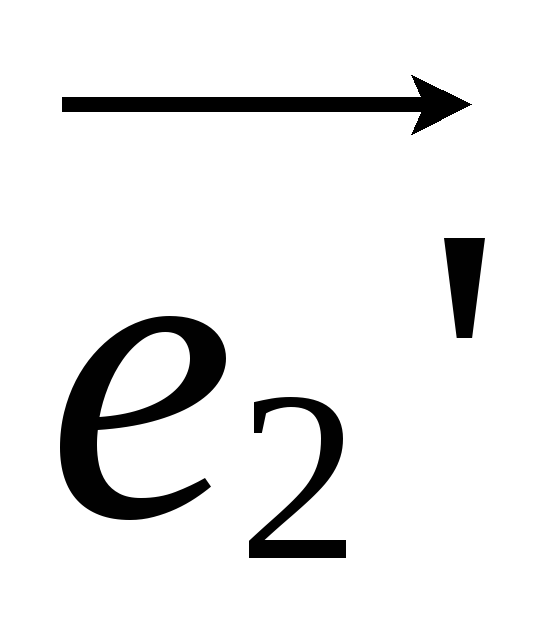в случае:

а) переноса начала;

б) замены координатных векторов.

§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат

Понятие направленного угла между векторами вводится на ориентированной плоскости.

Пусть и- ненулевые векторы, заданные в определенном порядке (- первый вектор,- второй вектор).

Если||, тонаправленным углом между вектором и вектором называется

величина , если базис,- правый;

величина , если базис,- левый.

Если , тонаправленный угол между ними считается равным , если, то(рис. 43).

Направленный угол между вектором и вектором обозначается так:

.

На чертеже направленный угол между векторами ипоказывают дугой со стрелкой, идущей от первого вектора ко второму.

Из определения направленного угла между векторами иследует, что он находится в следующих пределах:

.

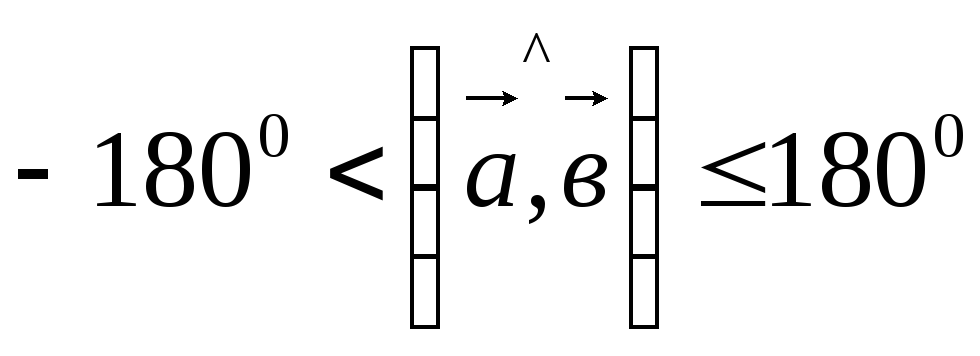Рассмотрим две прямоугольные декартовы системы координат и. ПустьМ(х;у) в ,в. Так как прямоугольная система координат - частный случай аффинной, то можно пользоваться формулами (5) из §12, но коэффициенты,,, уже не могут быть произвольными.

Найдем координаты векторов ,в старой системе. Рассмотрим два случая.

1. Базисы ,и,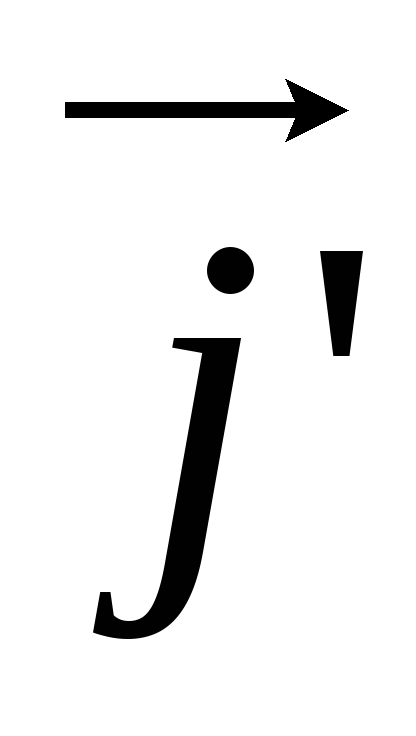одинаково ориентированы (рис. 44).

Пусть направленный угол . Приведем векторыик общему началуО (рис. 45).

Прямоугольные треугольники иравны по гипотенузе и острому углу (,), следовательно,и.

Из находим:

;

.

Следовательно, .

; .

Следовательно, . Тогда формулы (5) примут вид:

;

. (8)

Заметим, что определитель матрицы перехода от базиса ,к базису,

.

2) Базисы ,и,противоположно ориентированы (рис. 46).

Пусть. Приведем векторыик общему началуО (рис. 47).

Рассуждая аналогично случаю 1), получим:

;

;

; .

Следовательно, ;.

Тогда формулы (5) примут вид:

;

. (9)

Заметим, что определитель матрицы перехода от базиса ,к базису,в этом случае

.

Формулы (8) и (9) можно объединить:

, , если базисы ,и,одинаково ориентированы, , г , если базисы ,и,противоположно ориентированы. де

.

Частные случаи преобразования прямоугольной системы координат

1. Перенос начала: ,.

.

2. Поворот координатных векторов на угол : ,.