13 Операторные уравнения
Получение операторных уравнений элементов САР рассмотрим на следующих примерах.
1) Пусть имеется уравнение одноемкостного объекта.
(1)
Используя свойство преобразования Лапласа заменим каждый член уравнения его изображением по Лапласу.
(2)
(3)
Уравнение в передаточной функции ПНД – закона регулирования
Рассмотрим общий случай звена с одним входом и одним выходом, которое описывается дифференцированным уравнением
Общий вид оператора уравнения звена с данным входом и одним выходом.
-
собственный оператор звена, отражающий
его внутреннее свойства, например,
устойчивость
К(S) - оператор воздействия
Оператор уравнения такого звена имеет вид:
,
где 
- собственный оператор звена, определяющийся
выражением (7)
-
оператор воздействия по входному
сигналу, определяющийся выражением
(8).
Для одноемкостного объекта, которое является звеном, с двумя входными воздействиями
14 Передаточные функции
Пусть имеется звено САР с одним входом и одним выходом
Для этого звена найдено его операторное уравнение.
(1)
Найдем изображение выходного сигнала в явном виде:
(2)
Обозначим:
(3)
-
передаточная функция звена,
тогда:
(4)
Передаточной функцией называется операторное выражение, переводящее изображение входного сигнала звена в изображение входного сигнала.
Передаточной функцией называется отношение изображений по Лапласу выходного и входного сигналов звена.
Уравнение в передаточной функции ПНД – закона регулирования.
Из операторного уравнения звена запаздывания:
Передаточная функция общего звена с одним входом:
Для звена с несколькими входами уравнение в передаточных функциях имеет вид:
где
-
передаточная функция звена по воздействию
Пример: для одноемкостного объекта с операторным уравнением
Общий вид уравнения ОР в передаточных функциях.
-
передаточная функция ОР по регулируемому
воздействию
-
передаточная функция ОР по нагрузке
Пример:
Для звеньев САУ, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами, их передаточные функции являются дробно – радикальными выражениями комплексной переменной .
Передаточная функция звена запаздывания является трансцендентной.
15 Структурные системы
Для САР составляем структурные системы, которые в наглядной форме отражают состав элементов взаимосвязи между элементами.
Структурные системы соответствуют дифференциальным уравнениям, операторным уравнениям и передаточным функциям.
Преобразования структурных схем с помощью набора правил позволяет достаточно просто находить передаточные функции регуляторов разомкнутых и замкнутых систем.
Покажем составление структурной схемы на примере САР частоты вращения турбогенератора.
Полагаем, что для элементов САР получены на уравнения в передаточных функциях
Строим структурную схему, используя передаточные функции элементов.
На структурных схемах обозначаются величины, а не их изображения.
Структурные схемы содержат следующие элементы.
1) звенья направленного действия, характеризуемые передаточными формулами.
2) Элемент суммирования.
Элемент вычитания.
4) Линии связи показывают направление передачи сигналов и соединение элементов.
5) Точки разветвления сигналов, из которых сигнал расходится по ?????
Для упрощения структурных схем получения передаточных функций САР применяют преобразование структурных схем, эти преобразования базируются на решении операторных уравнений
1) Последовательное соединение звеньев.
Требуется заменить цепочку одним звеном, выполняющим такое преобразование сигнала Х в сигнал Y, что и исходная цепочка.
Подставим последовательно каждое предыдущее уравнение в последующее
W(s) - передаточная функция последовательного соединения звеньев.
Пример
7) Параллельное соединение звеньев
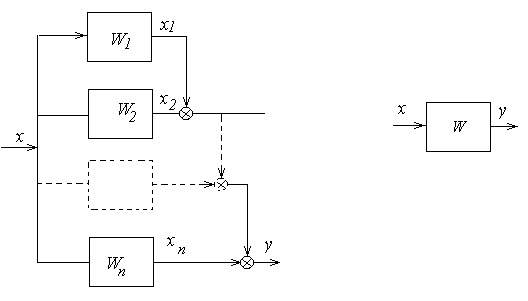
подставляем все уравнения в последнее и получим.
Пример
3) перенос точки разветвления с выходного сигнала звена на входной.
перенос точки разветвления с входного сигнала звена на выходной
замкнутый контур с ООС
Пример
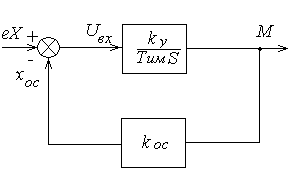
проверить
6) замкнутый контур с ПОС.
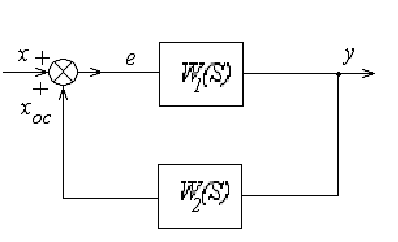
Проведя аналогичные выкладки можно получить.
7) Замкнутый контур с единичной отрицательной обратной связью.
8) Замкнутый контур с единичной ПОС
