23 Усилительное звено

В соответствии с определением это звено описывается уравнением:

(1)

- коэффициент передачи звена (коэффициент усиления)

Операторное уравнение звена:

(2)

Передаточная функция звена:

Примером такого могут служить безъемкостные объекты, датчики, усилители.

Разгонная характеристика звена, представляющая собой изменение выходного сигнала при скачкообразном изменении выходного.

Если разгонная характеристика получена экспериментально, то реальный коэффициент передачи:

Частотная передаточная функция звена:

АФЧХ звена.

- амплитудная характеристика звена.

- фазовая характеристика звена.

24 Интегрирующее звено

Звено описывается уравнением:

(1)

Т – постоянная времени звена

(2)

- начальное значение выходного сигнала.

Операторное уравнение звена:

Передаточная функция звена:

(3)

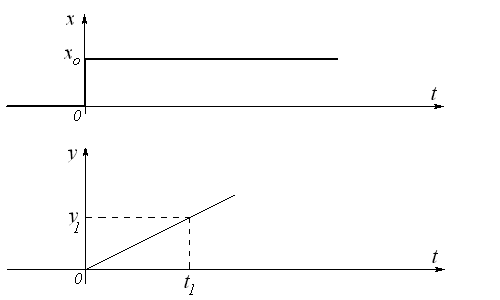
Разгонная характеристика звена найдется из (2) при (4)

(5)

Измерим выходной сигнал y₁ в произвольный момент времени t₁

Реальная постоянная времени звена

Частотная передаточная функция звена.

ВЧХ:

МЧХ:

АФЧХ:

ФЧХ:

ЛАЧХ:

26 Колебательное звено

Это звено описывается следующим диф. уравнением 2-го порядка.

(1)

,- постоянные времени звена

- коэффициент передачи

Обозначим: - коэффициент затухания

Колебательность звена определяется значением

Составим характеристическое уравнение звена:

(2)

(3)

Характеристическое уравнение имеет вещественные корни для и комплексные корни для

Найдем для уравнения (2) его операторную форму:

(4)

Передаточная функция звена

(5)

В случае вещественных корней

,

Что соответствует последовательному соединению двух инерционных звеньев.

Т.о. при звено не является колебательным.

В случае переходная функция звена определяется выражением:

где - собственная угловая частота звена.

- начальная фаза

Графики переходных функций.

Частотная передаточная функция звена.

ВЧХ:

МЧХ:

:

ЛАЧХ:

Найдем компоненты ЛАЧХ:

27 Идеальное дифференцирующее звено

(1)

Операторное уравнение звена:

(2)

(3)

Разгонная характеристика звена:

Выходной сигнал звена будет представлять собой - функцию.

Рассмотрим поведение выходного сигнала при линейном изменении входного.

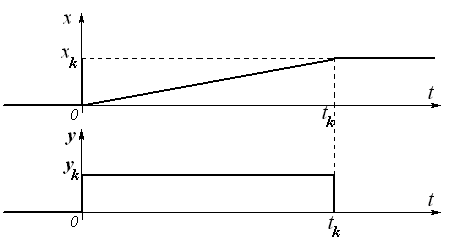
, , где

- скорость изменения сигнала;

Если эти графики получены экспериментально, то

Частотная передаточная функция звена.

ВЧХ:

МЧХ:

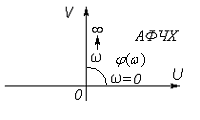
АЧХ:

ФЧХ:

ЛАЧХ:

28 Реальное дифференцирующее звено

(1)

- время дифференцирования

- инерционная постоянная времени (пост. времени фильтра)

Операторное уравнение звена:

(2)

(3)

Разгонная характеристика звена:

Для определения разгонной характеристики надо решить уравнение (1), когда на его вход подается  - функция.

Изменение сигнала y в этом случае будет определяться выражением

(4)

(5)

(6)

Экспериментально пост. времени может быть определена графически, апо формуле (6)

Частотная передаточная функция звена:

ВЧХ:

МЧХ:

:

; ;

АЧХ:

ФЧХ:

ЛАЧХ; ЛФЧХ:

Представим звено в виде последовательного соединения двух звеньев, дифференцирующего и инерционного.

В этом случае ЛАЧХ реального дифференцирующего звена будет представлять собой сумму ЛАЧХ двух звеньев, которые известны.

ЛФЧХ также будут представлять сумму ЛФЧХ этих же звеньев.

Где индексом "д" обозначена ЛЧХ идеального диф. звена, а индексом "ин" инерционного.

Пусть

Если частотные характеристики звена определены экспериментально, то по графикам ЛЧХ можно определить значение и.