Связь между потенциалом и вектором.

Электрическое поле полностью описывается векторной функцией , которая позволяет найти силу, действующую на точечный заряд в любой точке поля, вычислить работу сил поля при перемещении заряда и др. Введение потенциала позволяет просто вычислить работу по перемещению заряда:

,

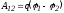кроме того, зная потенциал , можно восстановить поле.

Приращение потенциала равно:

.

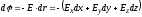следовательно,

,,,

где символ частной производной подчеркивает, что функцию надо дифференцировать, например, по, считаяипри этом постоянными.

Таким образом, вектор можно представить в виде:

.

Напряженность поля равна со знаком минус градиенту потенциала.

Зная 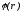, по этой формуле можно восстановить поле.

Рассмотрим несколько примеров.

1. Найти напряженность поля, потенциал которого имеет вид:, где- постоянный вектор.

Представим ,

где 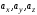- постоянные.

Найдём проекции:

,,,

следовательно, .

Видно, что поле является однородным.

2. Напряженность поля на оси кольца. Зная потенциал поля на оси кольца , легко найти зависимость, взяв производную с обратным знаком:

.

Этот же результат мы получили, используя принцип суперпозиции.

3. Аналогично можно получить выражение для 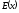поля на оси круга.

Убедитесь в этом самостоятельно.

Эквипотенциальные поверхности.

Наглядно электростатическое поле можно изобразить с помощью эквипотенциальных поверхностей. Это поверхность, в каждой точке которой потенциал имеет одно и то же значение. Убедимся, что векторнаправлен в каждой точке по нормали к эквипотенциальной поверхности в сторону уменьшения потенциала. Представим соотношение:

,

в следующем виде:

,

где ,- проекция на направление перемещения, которая равна:

.

Проекция вектора на направление перемещенияравна со знаком минус производной от потенциала по данному направлению. Знак минус перед производной указывает, что напряженность направлена в сторону убыли потенциала.

При перемещении вдоль эквипотенциальной поверхности в любом направлении

,

т.к. .

Следовательно, составляющая вектора на любое направление касательное к эквипотенциальной поверхности равно нулю. А это означает, что векторперпендикулярен к эквипотенциальной поверхности в каждой её точке.

При перемещении вдоль нормали к эквипотенциальной поверхности в сторону уменьшения потенциала нормальная составляющая будет положительной величиной, т.е. векторнаправлен в сторону уменьшения потенциала, противоположно вектору.

Эквипотенциальные поверхности проводятся таким образом, чтобы разность потенциалов для двух соседних поверхностей была одинаковой. Тогда по густоте эквипотенциальных поверхностей можно наглядносудить о значении напряженности поля в разных точках. Там, где эти поверхности расположены гуще, там напряженность поля больше, а силовые линии ортогональны этим поверхностям.

Примеры.

Графическое изображение поля точечного заряда и поля диполя.

Проводник в электрическом поле.

При внесении проводника в электрическое поле происходит смещение положительных и отрицательных зарядов (ядер и электронов), что приводит к разделению этих зарядов. Это явление называется электростатической индукцией,а появившиеся в результате разделения заряды –индуцированными зарядами,которые создают дополнительное электрическое поле. Суммарное поле внешнего поля и поля индуцированных зарядов образуют результирующее поле при наличии вещества.