
- •Федеральное агентство по образованию
- •Предмет курса «Электромагнетизм».
- •Основные понятия и законы. Электрический заряд и его свойства.
- •Взаимодействие заряженных частиц. Закон Кулона (1785г).
- •Электрическое поле неподвижного точечного заряда.
- •Принцип суперпозиции для напряжённости.
- •Электрическое поле точечного диполя.
- •Особенности расчёта напряжённости электрического поля при непрерывном пространственном распределении заряда.
- •Электрическое поле на оси равномерно заряженного тонкого кольца.
- •Электрическое поле на оси равномерно заряженного круга.
- •Электрическое поле равномерно заряженной нити ().
- •Частные случаи.
- •Теорема Гаусса.
- •Применение теоремы Гаусса.
- •Теорема о циркуляции вектора электростатического поля. Понятие потенциала.
- •Понятие потенциала.
- •Потенциал поля точечного заряда.
- •Потенциал поля системы зарядов.
- •Связь между потенциалом и вектором.
- •Эквипотенциальные поверхности.
- •Проводник в электрическом поле.
- •Поле внутри и снаружи проводника.
- •Поле у поверхности проводника.
- •Силы, действующие на поверхность проводника.
- •Свойства замкнутой проводящей оболочки.
- •Общая задача электростатики.
- •Понятие электроемкости. Конденсаторы.
- •Конденсаторы.
- •Ёмкость плоского конденсатора.
- •Ёмкость сферического конденсатора.
- •Вектор поляризации (поляризованность).
- •Поле в диэлектрике.
- •Диэлектрическая восприимчивость и её связь с диэлектрической проницаемостью.
- •Вектор электрической индукции .
- •Физические условия на границе раздела диэлектриков.
- •Энергия электрического поля.
- •Работа поля при поляризации диэлектрика.
- •Электрическая энергия системы зарядов.
- •Примеры.
- •Постоянный ток. Электрический ток.
- •Сила тока.
- •Плотность тока.
- •Закон Ома для однородного проводника.
- •Закон Ома в дифференциальной форме.
- •Закон Ома для участка, содержащего сторонние силы.
- •Закон Ома в интегральной форме для участка, содержащего источник тока.
- •Закон Ома для замкнутой цепи.
- •Соединение проводников.
- •Закон Джоуля - Ленца.
- •Разветвленные цепи. Правила Кирхгофа.
- •Примеры и задачи для самостоятельного решения.
- •Магнетизм. Магнитное поле.
- •Графическое изображение постоянного магнитного поля.
- •Примеры движения заряженных частиц в электромагнитном поле.
- •Задачи для самостоятельного решения.
- •Закон Био-Савара-Лапласа и принцип суперпозиции.
- •Принцип суперпозиции для вектора .
- •Магнитное поле в веществе (предварительные сведения).
- •Примеры расчета магнитных полей постоянных токов.
- •Задачи для самостоятельного решения.
- •Основные законы магнитного поля. Теорема Гаусса для вектора .
- •Теорема о циркуляции вектора .
- •Применение теоремы о циркуляции вектора .
- •Задачи для самостоятельного решения.
- •Сила Ампера. Закон Ампера.
- •Момент сил, действующий на контур с током.
- •Работа по перемещению контура с током в постоянном магнитном поле.
- •Взаимодействие токов.
- •Примеры
- •Задачи для самостоятельного решения.
- •Вещество в магнитном поле.
- •Вектор напряженности магнитного поля . Теорема о циркуляции вектора .
- •Связь между и,и.
- •Применение теоремы о циркуляции .
- •Электромагнетизм. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
- •Природа сторонних сил в явлении электромагнитной индукции.
- •Явление самоиндукции.
- •Энергия магнитного поля.
- •Примеры проявления самоиндукции.
- •Явление взаимной индукции. Взаимная индуктивность. Эдс взаимной индукции.
- •Явление магнитоэлектрической индукции. Токи смещения.
- •Теорема полного тока.
- •Уравнения Максвелла в интегральной форме.
Частные случаи.
а) Поле бесконечной прямой нити.
Положив
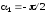 ,
,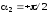 ,
,
Находим
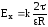 ,
,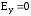 ,
,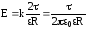 .
.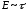 ,
,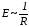 .
.
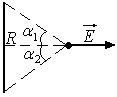
б) Напряженность электрического поля в точках равноудаленных от концов прямой ити.
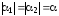 ,
, ,
,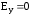 .
.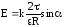 .
.
Для
малых углов
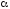 получаем закон обратных квадратов:
получаем закон обратных квадратов:
 ,
так как
,
так как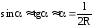 .
.
Лекция 3.
Поток
вектора напряженности
 .
.
Величина напряженности равна числу силовых линий, пересекающих единичную поверхность, перпендикулярную силовым линиям в данном месте.
Число силовых линий, которые пересекают реальную или воображаемую поверхность, называется потоком вектора напряженности.
Число силовых линий, пронизывающих
элементарную площадку
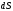 ,
нормаль к которой
,
нормаль к которой составляет угол
составляет угол с направлением вектора напряженности
с направлением вектора напряженности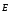 в данном месте равно:
в данном месте равно: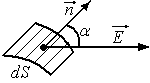
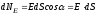 ,
,
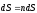 ,
,
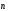 -единичный
вектор, перпендикулярный элементарной
площадке, выбор направления которого
условен.
-единичный
вектор, перпендикулярный элементарной
площадке, выбор направления которого
условен.
Если имеется некоторая произвольная
поверхность S, то поток
вектора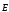 сквозь нее равен:
сквозь нее равен:
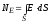 .
.
Поток
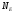 величина алгебраическая, знак которой
зависит не только от конфигурации поля
величина алгебраическая, знак которой
зависит не только от конфигурации поля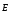 ,
но и от выбора направления нормали. В
случае замкнутых поверхностей принято
нормаль выбирать в направлении наружной
области пространства.
,
но и от выбора направления нормали. В
случае замкнутых поверхностей принято
нормаль выбирать в направлении наружной
области пространства.
Поток через замкнутую поверхность будем представлять интегралом:
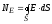 ,
,
где кружок у интеграла означает, что интегрирование проводится по замкнутой поверхности.
Теорема Гаусса.
Поток вектора
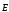 через замкнутую поверхность зависит
только от алгебраической суммы зарядов,
охваченных этой поверхностью. А именно:
через замкнутую поверхность зависит
только от алгебраической суммы зарядов,
охваченных этой поверхностью. А именно:
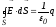 ,
,
где
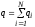 - алгебраическая сумма точечных зарядов,
охваченных замкнутой поверхностью,
или:
- алгебраическая сумма точечных зарядов,
охваченных замкнутой поверхностью,
или: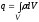 -
в случае непрерывного распределенного
заряда в объеме
-
в случае непрерывного распределенного
заряда в объеме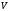 ,
ограниченного замкнутой поверхностью.
,
ограниченного замкнутой поверхностью.
При наличии однородного изотропного диэлектрика этот поток равен:
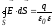 .
.
Доказательство.
Эта теорема является интегральным выражением закона Кулона и отражает то обстоятельство, что источниками и стоками электрического поля являются электрические заряды.
Рассмотрим поток
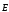 через сферическую поверхность, в центре
которого находится точечный зарядq:
через сферическую поверхность, в центре
которого находится точечный зарядq: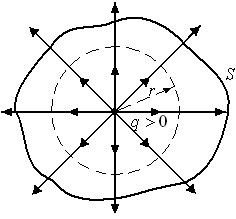
 .
.
Для напряженности можно записать:
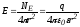 .
.
Откуда следует:
 ,
,
где
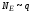 .
.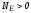 ,
еслиq>0 и
,
еслиq>0 и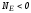 ,
еслиq<0. Положительный
заряд является источником силовых линий
поля, отрицательный – стоком.
,
еслиq<0. Положительный
заряд является источником силовых линий
поля, отрицательный – стоком.
Число силовых линий, пресекающих
сферическую поверхность, равно числу
силовых линий, исходящих из точечного
заряда.
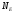 не
зависит от радиуса сферы. Таким образом,
поток
не
зависит от радиуса сферы. Таким образом,
поток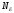 не
зависит от размеров сферической
поверхности, более того, от формы
замкнутой поверхности, которая охватывает
точечный заряд. Все силовые линии,
прошедшие сквозь сферическую поверхность,
пересекут произвольную поверхность
не
зависит от размеров сферической
поверхности, более того, от формы
замкнутой поверхности, которая охватывает
точечный заряд. Все силовые линии,
прошедшие сквозь сферическую поверхность,
пересекут произвольную поверхность .
.
Если произвольная замкнутая поверхность
охватывает систему точечных зарядов,
то, очевидно, результирующий поток будет
равен алгебраической сумме потоков от
всех точечных зарядов через эту
поверхность: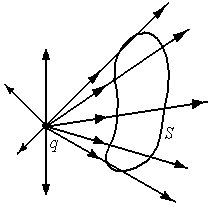
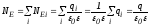 .
.
Что и требовалось доказать.
Поток
 через
замкнутую поверхность для зарядов,
находящихся вне этой поверхности равен
нулю (см. рисунок), так как число силовых
линий входящих и выходящих одинаково.
через
замкнутую поверхность для зарядов,
находящихся вне этой поверхности равен
нулю (см. рисунок), так как число силовых
линий входящих и выходящих одинаково.
Применение теоремы Гаусса.
Поскольку поле
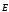 зависит от положения всех зарядов,
теорема Гаусса, не позволяет определить
в общем случае это поле. Однако, в
некоторых случаях она позволяет получать
ответы на некоторые принципиальные
вопросы, не решая задачи, а также находить
само поле
зависит от положения всех зарядов,
теорема Гаусса, не позволяет определить
в общем случае это поле. Однако, в
некоторых случаях она позволяет получать
ответы на некоторые принципиальные
вопросы, не решая задачи, а также находить
само поле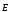 ,
минуя принцип суперпозиции, чрезвычайно
простым путем, если в распределении
зарядов имеется некоторая симметрия.
Рассмотрим несколько примеров.
,
минуя принцип суперпозиции, чрезвычайно
простым путем, если в распределении
зарядов имеется некоторая симметрия.
Рассмотрим несколько примеров.
Может ли система точечных зарядов быть устойчивой?Ответ нет, так как для устойчивого положения, например, положительного заряда
 ,
необходимо, чтобы во всех точках
поверхности
,
необходимо, чтобы во всех точках
поверхности поле
поле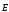 ,
образованное остальными зарядами
системы, было направлено к заряду
,
образованное остальными зарядами
системы, было направлено к заряду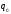 .
Но такая конфигурация поля
.
Но такая конфигурация поля противоречит теореме Гаусса.
противоречит теореме Гаусса.
Поле равномерно заряженной плоскости.
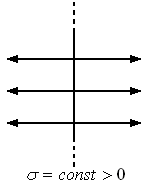
Из
симметрии задачи следует, что силовые
линии поля
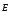 перпендикулярны плоскости. Такая
конфигурация поля подсказывает, что в
качестве замкнутой поверхности можно
выбрать прямой цилиндр, как показано
на рисунке. Поток через боковую поверхность
цилиндра равен нулю, и поэтому поток
через всю поверхность цилиндра равен
перпендикулярны плоскости. Такая
конфигурация поля подсказывает, что в
качестве замкнутой поверхности можно
выбрать прямой цилиндр, как показано
на рисунке. Поток через боковую поверхность
цилиндра равен нулю, и поэтому поток
через всю поверхность цилиндра равен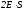 ,
который равен согласно теореме Гаусса
,
который равен согласно теореме Гаусса .
Откуда следует
.
Откуда следует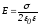 .
Этот результат мы уже получили, используя
принцип суперпозиции. Так как
.
Этот результат мы уже получили, используя
принцип суперпозиции. Так как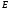 не зависит от расстояния до пластины,
электрическое поле пластины является
однородным. Полученный результат
справедлив только для бесконечной
плоской поверхности. В случае конечной
пластины, полученное значениеEсправедливо для точек вблизи середины
пластины, вдали от ее краев.
не зависит от расстояния до пластины,
электрическое поле пластины является
однородным. Полученный результат
справедлив только для бесконечной
плоской поверхности. В случае конечной
пластины, полученное значениеEсправедливо для точек вблизи середины
пластины, вдали от ее краев.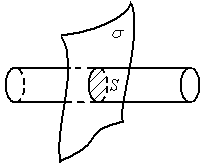
Поле двух параллельных плоскостей, заряженных равномерно разноименными зарядами с поверхностной плоскостью зарядов
 и
и .
.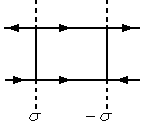
Это
поле можно найти как суперпозицию полей,
создаваемых каждой плоскостью в
отдельности. Вне пластин поля пластин
противоположны, а между пластинами
направлены в одну сторону. Напряженность
поля вне пластин равна нулю, а между
пластинами
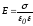 при наличии однородного изотропного
диэлектрика.
при наличии однородного изотропного
диэлектрика.
Электрическое поле пластины, равномерно заряженной по объему
 .
.
Электрическое
поле такой пластины обладает плоской
симметрией E(x)
и силовые линии направлены вдоль осиx. Очевидно, приx= 0E= 0. Выбирая замкнутую
поверхность в форме прямого цилиндра
с образующей вдоль осиxпо теореме Гаусса для точек внутри
пластины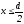 :
:
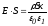 ,
,
вне
пластины
 :
:
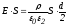 .
.
Откуда находим

 ,
где
,
где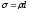 .
.
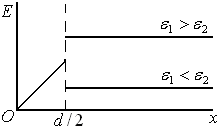
Электрическое
поле внутри пластины увеличивается
пропорционально

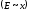 ,
а вне пластины электрическое поле не
зависит от расстоянияxи является однородным. На границе
,
а вне пластины электрическое поле не
зависит от расстоянияxи является однородным. На границе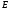 испытывает разрыв (см. рисунок).
испытывает разрыв (см. рисунок).
Поле бесконечного цилиндра, заряженного равномерно по поверхности с линейной плотностью
 .
.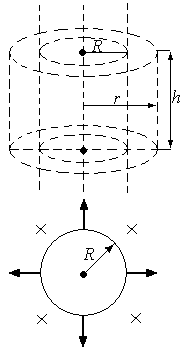
Очевидно,
электрическое поле такого цилиндра
обладает осевой симметрией, т.е.
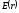 ,
где
,
где – расстояние от оси цилиндра (см. на
рисунке электрическое поле цилиндра в
поперечном разрезе).
– расстояние от оси цилиндра (см. на
рисунке электрическое поле цилиндра в
поперечном разрезе).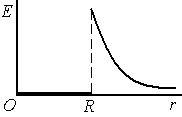
Замкнутую
поверхность целесообразно выбирать в
форме коаксильного цилиндра высотой
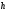 и радиусом
и радиусом (см. рисунок). По теореме Гаусса в случае
(см. рисунок). По теореме Гаусса в случае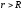 имеем
имеем
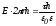 ,
откуда:
,
откуда:
 .
.
Для точек внутри цилиндра
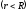 напряженность электрического поля
равна нулю, так как замкнутая поверхность
не содержит внутри зарядов. Зависимость
напряженность электрического поля
равна нулю, так как замкнутая поверхность
не содержит внутри зарядов. Зависимость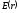 имеет вид (см. рисунок). Вне цилиндра
электрическое поле подобно полю нити,
расположенной вдоль оси цилиндра.
имеет вид (см. рисунок). Вне цилиндра
электрическое поле подобно полю нити,
расположенной вдоль оси цилиндра.
Электрическое поле цилиндра, равномерно заряженного по объему
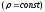 .
.
Электрическое
поле такого цилиндра обладает осевой
симметрией
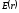 ,
где
,
где – расстояние от оси цилиндра. Выбирая
замкнутые поверхности в форме коаксильных
цилиндров, по теореме Гаусса для точек
вне цилиндра (
– расстояние от оси цилиндра. Выбирая
замкнутые поверхности в форме коаксильных
цилиндров, по теореме Гаусса для точек
вне цилиндра ( –
радиус цилиндра):
–
радиус цилиндра):
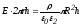 ,
,
для точек внутри цилиндра:
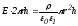 ,
,
где
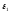 и
и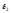 -
диэлектрические проницаемости цилиндра
и окружающей среды,
-
диэлектрические проницаемости цилиндра
и окружающей среды, – высота коаксильного цилиндра.
– высота коаксильного цилиндра.
Поле такого цилиндра описывается следующими соотношениями:
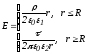 ,
где
,
где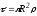 -
линейная плотность заряда цилиндра.
-
линейная плотность заряда цилиндра.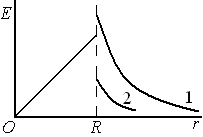
Внутри
цилиндра электрическое поле растет
пропорционально

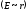 ,
вне цилиндра убывает
,
вне цилиндра убывает аналогично
полю нити, расположенной вдоль оси
цилиндра. На границе раздела
аналогично
полю нити, расположенной вдоль оси
цилиндра. На границе раздела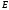 испытывает разрыв.
испытывает разрыв.
Поле сферической поверхности, заряженной равномерно
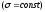 зарядомq. Это
поле обладает сферической симметрией,
т.е.
зарядомq. Это
поле обладает сферической симметрией,
т.е. ,
где
,
где – расстояние от центра сферы. Естественно,
в качестве замкнутой поверхности
выбрать концентрическую сферу. Для
точек вне сферы (
– расстояние от центра сферы. Естественно,
в качестве замкнутой поверхности
выбрать концентрическую сферу. Для
точек вне сферы (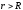 – радиус сферы) по теореме Гаусса:
– радиус сферы) по теореме Гаусса:
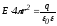 ,
где
,
где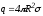 .
.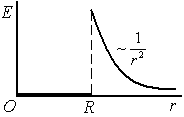
Откуда:
 .
.
Для всех точек внутри сферы
 напряженность равна нулю. Зависимость
напряженность равна нулю. Зависимость представлена на рисунке. Вне сферы
электрическое поле аналогично полю
точечного заряда, находящегося в центре
сферы.
представлена на рисунке. Вне сферы
электрическое поле аналогично полю
точечного заряда, находящегося в центре
сферы.
Электрическое поле шара, равномерно заряженного по объему
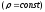 .
.
Поле
такого шара обладает сферической
симметрией
 ,
где
,
где - расстояние от центра шара. Диэлектрическая
проницаемость материала шара
- расстояние от центра шара. Диэлектрическая
проницаемость материала шара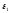 ,
а окружающей среды
,
а окружающей среды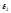 .
Выбирая замкнутые поверхности в форме
концентрических сфер, для точек внутри
шара (
.
Выбирая замкнутые поверхности в форме
концентрических сфер, для точек внутри
шара ( – радиус шара) по теореме Гаусса:
– радиус шара) по теореме Гаусса: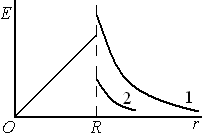
 ,
,
а
для точек вне шара
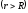 :
:
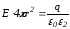 ,
где
,
где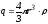 .
.
Откуда следует:
 .
.
Зависимость
 представлена на рис. Внутри шара
представлена на рис. Внутри шара ,
а вне шара
,
а вне шара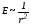 .На
границе раздела диэлектриков
.На
границе раздела диэлектриков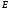 испытывает скачок (разрыв), кривая 1
соответствует значениям
испытывает скачок (разрыв), кривая 1
соответствует значениям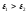 ,
кривая 2 значениям
,
кривая 2 значениям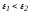 .
.
Лекция 4.
