
- •Федеральное агентство по образованию
- •Предмет курса «Электромагнетизм».
- •Основные понятия и законы. Электрический заряд и его свойства.
- •Взаимодействие заряженных частиц. Закон Кулона (1785г).
- •Электрическое поле неподвижного точечного заряда.
- •Принцип суперпозиции для напряжённости.
- •Электрическое поле точечного диполя.
- •Особенности расчёта напряжённости электрического поля при непрерывном пространственном распределении заряда.
- •Электрическое поле на оси равномерно заряженного тонкого кольца.
- •Электрическое поле на оси равномерно заряженного круга.
- •Электрическое поле равномерно заряженной нити ().
- •Частные случаи.
- •Теорема Гаусса.
- •Применение теоремы Гаусса.
- •Теорема о циркуляции вектора электростатического поля. Понятие потенциала.
- •Понятие потенциала.
- •Потенциал поля точечного заряда.
- •Потенциал поля системы зарядов.
- •Связь между потенциалом и вектором.
- •Эквипотенциальные поверхности.
- •Проводник в электрическом поле.
- •Поле внутри и снаружи проводника.
- •Поле у поверхности проводника.
- •Силы, действующие на поверхность проводника.
- •Свойства замкнутой проводящей оболочки.
- •Общая задача электростатики.
- •Понятие электроемкости. Конденсаторы.
- •Конденсаторы.
- •Ёмкость плоского конденсатора.
- •Ёмкость сферического конденсатора.
- •Вектор поляризации (поляризованность).
- •Поле в диэлектрике.
- •Диэлектрическая восприимчивость и её связь с диэлектрической проницаемостью.
- •Вектор электрической индукции .
- •Физические условия на границе раздела диэлектриков.
- •Энергия электрического поля.
- •Работа поля при поляризации диэлектрика.
- •Электрическая энергия системы зарядов.
- •Примеры.
- •Постоянный ток. Электрический ток.
- •Сила тока.
- •Плотность тока.
- •Закон Ома для однородного проводника.
- •Закон Ома в дифференциальной форме.
- •Закон Ома для участка, содержащего сторонние силы.
- •Закон Ома в интегральной форме для участка, содержащего источник тока.
- •Закон Ома для замкнутой цепи.
- •Соединение проводников.
- •Закон Джоуля - Ленца.
- •Разветвленные цепи. Правила Кирхгофа.
- •Примеры и задачи для самостоятельного решения.
- •Магнетизм. Магнитное поле.
- •Графическое изображение постоянного магнитного поля.
- •Примеры движения заряженных частиц в электромагнитном поле.
- •Задачи для самостоятельного решения.
- •Закон Био-Савара-Лапласа и принцип суперпозиции.
- •Принцип суперпозиции для вектора .
- •Магнитное поле в веществе (предварительные сведения).
- •Примеры расчета магнитных полей постоянных токов.
- •Задачи для самостоятельного решения.
- •Основные законы магнитного поля. Теорема Гаусса для вектора .
- •Теорема о циркуляции вектора .
- •Применение теоремы о циркуляции вектора .
- •Задачи для самостоятельного решения.
- •Сила Ампера. Закон Ампера.
- •Момент сил, действующий на контур с током.
- •Работа по перемещению контура с током в постоянном магнитном поле.
- •Взаимодействие токов.
- •Примеры
- •Задачи для самостоятельного решения.
- •Вещество в магнитном поле.
- •Вектор напряженности магнитного поля . Теорема о циркуляции вектора .
- •Связь между и,и.
- •Применение теоремы о циркуляции .
- •Электромагнетизм. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
- •Природа сторонних сил в явлении электромагнитной индукции.
- •Явление самоиндукции.
- •Энергия магнитного поля.
- •Примеры проявления самоиндукции.
- •Явление взаимной индукции. Взаимная индуктивность. Эдс взаимной индукции.
- •Явление магнитоэлектрической индукции. Токи смещения.
- •Теорема полного тока.
- •Уравнения Максвелла в интегральной форме.
Задачи для самостоятельного решения.
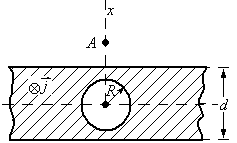
В неограниченном прямом цилиндрическом проводе имеется цилиндрическая полость, ось которой смещена относительно оси цилиндра на расстояние
 (см. рисунок). По цилиндру течет однородный
ток
(см. рисунок). По цилиндру течет однородный
ток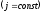 .
Определить индукцию магнитного поля
в точках внутри полости. Принять для
цилиндра
.
Определить индукцию магнитного поля
в точках внутри полости. Принять для
цилиндра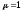 .
.
Ответ:
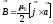 .
.
В неограниченной пластине имеется цилиндрическая полость радиусом
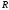 (см. рисунок). По пластине течет однородный
ток
(см. рисунок). По пластине течет однородный
ток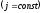 .
Определить индукцию магнитного поля
в точке
.
Определить индукцию магнитного поля
в точке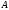 с координатой
с координатой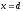 .
.
Ответ:
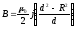 .
.
При решении предложенных задач воспользуйтесь методом вложения и используйте принцип суперпозиции.
Лекция 14.
Сила Ампера. Закон Ампера.
Каждый носитель тока испытывает действие
магнитной силы. Действие этой силы
передается проводнику, по которому
заряды движутся. В результате магнитное
поле действует с определенной силой на
проводник с током. Эта сила называется
силой Ампера. Найдем силу Ампера,
действующую на элементарный участок
тонкого проводника
 (вектор
(вектор направлен вдоль тока). Носители тока
движутся со скоростью
направлен вдоль тока). Носители тока
движутся со скоростью ,
где
,
где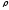 - объёмная плотность заряда носителей
тока. На заряд в объёме элементарного
участка:
- объёмная плотность заряда носителей
тока. На заряд в объёме элементарного
участка:
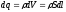 .
.
действует магнитная сила,
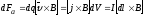 ,
,
где
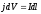 .
.
Векторы
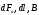 связаны
правилом правого буравчика.
связаны
правилом правого буравчика.
Последнее соотношение выражает закон Ампера. Модуль силы Ампера:
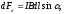
где
 - угол между направлением тока и магнитного
поля.
- угол между направлением тока и магнитного
поля.
При
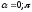 →
→ ,
,
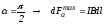 .
.
Сила, действующая на тонкий проводник
с током
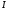 в магнитном поле, находится суммированием:
в магнитном поле, находится суммированием:
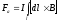 .
.
На прямой проводник в однородном магнитном поле действует сила Ампера:
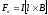 ,
,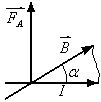
модуль которой
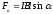 .
.
Результирующая сила Ампера, действующая на контур с током равна:
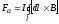 .
.
Если магнитное поле однородно, то результирующая сила Ампера равна нулю:
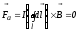 ,
,
так
как
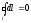 .
.
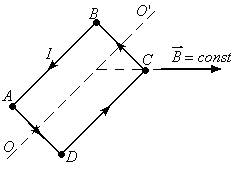
Момент сил, действующий на контур с током.
Рассмотрим плоский контур в форме
прямоугольника в однородном магнитном
поле (см. рисунок). В контуре поддерживается
постоянный ток
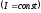 .
На стороны
.
На стороны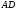 и
и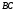 действуют
равные силы, направленные вдоль оси
действуют
равные силы, направленные вдоль оси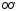 ,
эти силы не создают вращательного
момента относительно оси
,
эти силы не создают вращательного
момента относительно оси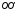 .
Силы, действующие на стороны
.
Силы, действующие на стороны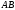 и
и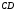 создают вращающий момент относительно
оси ОО’.
создают вращающий момент относительно
оси ОО’.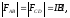 где
где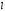 – длина стороны прямоугольника
– длина стороны прямоугольника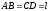 .
Момент этой пары сил равен:
.
Момент этой пары сил равен:
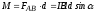 ,
,
где
 – длина сторон
– длина сторон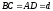 .
.
Учтём, что
 - площадь контура,
- площадь контура,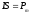 - магнитный момент контура. Для величины
вращательного момента получаем:
- магнитный момент контура. Для величины
вращательного момента получаем:
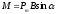 .
.
Вектор вращательного момента равен:
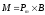 ,
,
так
как
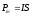 перпендикулярен плоскости контура и
связан с направлением тока в контуре
правилом правого буравчика, а угол
перпендикулярен плоскости контура и
связан с направлением тока в контуре
правилом правого буравчика, а угол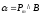 .
.
Отметим, что последнее соотношение пригодно для контура с током произвольной конфигурации.
Углу
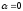 соответствует устойчивое равновесие
контура
соответствует устойчивое равновесие
контура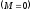 ,
а углу
,
а углу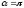 - неустойчивое равновесие. При
- неустойчивое равновесие. При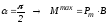 .
.
Свободный контур с током в магнитном поле будет совершать колебательное движение около положения равновесия согласно уравнению:
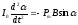 ,
,
где
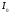 - момент инерции контура относительно
оси
- момент инерции контура относительно
оси .
.
При малых углах
 колебания будут гармоническими с угловой
частотой:
колебания будут гармоническими с угловой
частотой:
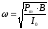 .
.
Если после прохождения положения равновесия изменить направление тока на противоположный, контур будет вращаться в прежнем направлении. В этом заключается физический принцип работы электрического двигателя постоянного тока, в котором электрическая энергия преобразуется в механическую.
Если площадь контура
 ,
то такой контур с током называют
элементарным. Элементарный контурный
ток полностью характеризуется магнитным
моментом
,
то такой контур с током называют
элементарным. Элементарный контурный
ток полностью характеризуется магнитным
моментом .
Атомы, молекулы, элементарные частицы
обладают магнитным моментом и поэтому
участвуют в магнитном взаимодействии.
Под действием внешнего магнитного поля
магнитные моменты ориентируются вдоль
внешнего поля усиливая в целом внешнее
магнитное поле, т.к. обладают собственным
магнитным полем. В этом заключается
физический механизм парамагнетика.
.
Атомы, молекулы, элементарные частицы
обладают магнитным моментом и поэтому
участвуют в магнитном взаимодействии.
Под действием внешнего магнитного поля
магнитные моменты ориентируются вдоль
внешнего поля усиливая в целом внешнее
магнитное поле, т.к. обладают собственным
магнитным полем. В этом заключается
физический механизм парамагнетика.
Отметим, что элементарный контурный ток в неоднородном магнитном поле не только поворачивается к положению устойчивого равновесия, но и под действием результирующей магнитной силы втягивается в область больших значений индукции магнитного поля. Рассмотреть самостоятельно.
