Принцип суперпозиции для вектора .

Опыт показывает, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитное поле, создаваемое совокупностью движущихся зарядов или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом ли током в отдельности:

,

.

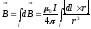Магнитное поле в веществе (предварительные сведения).

Вещество в магнитном поле намагничивается. При этом в объеме и на поверхности вещества возникают связанные токи (молекулярные токи), которые создают свое магнитное поле 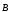. Магнитное поле в веществе равно сумме магнитного поля в вакуумеи поля молекулярных токов:

.

В однородном изотропном веществе (магнетике) магнитное поле молекулярных токов может быть направлено вдоль(парамагнетики) или против (диамагнетики).

Отношение 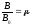называется магнитной проницаемостью, которая зависит от природы магнетика и его термического состояния.- величина безразмерная. Для парамагнетиков, а для диамагнетиков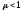. Существуют магнетики, у которых наблюдается остаточная намагниченность и. К ним относятся железо, кобальт, никель и их сплавы. Они получили наименование – ферромагнетики.

Примеры расчета магнитных полей постоянных токов.

1. Магнитное поле прямого тока.

Рассмотрим прямолинейный участок тонкого провода, по которому течет постоянный ток (см. рисунок). Найдёмв произвольной точке пространства, удаленной от проводника на расстояние, а концам участка соответствуют полярные углыи.

Вектор перпендикулярен плоскости листа, что условно обозначено знаком. Силовые линииявляются окружностями.

Величина магнитного поля элементарного участка токав выделенной точке пространства равна:

.

Здесь учтено, что .

Интегрируя от донаходим величину индукции магнитного поля в исследуемой точке:

.

В частном случае бесконечного прямого тока :

.

Другие частные случаи исследуйте самостоятельно.

2. Магнитное поле на оси кругового тока в однородном изотропном магнетике.

Выделим элементарный участок кругового тока (см. рисунок). Величина индукции в точкена осиот элементарного участка равна:

,

где .

От всех элементов тока будет образовываться конус векторов , а результирующий векторбудет направлен вдоль оси. Это означает, что для нахождения модуля векторадостаточно сложить проекции векторовна ось. Каждая такая проекция равна:

,

где .

Интегрируя последнее соотношение по всем элементам dl, находим:

.

В центре кругового тока :

.

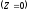Для всех точек на оси при :

.

Произведение силы тока Iна площадь кругового тока называется магнитным моментом кругового тока.

Индукция магнитного поля в точках на оси кругового тока пропорциональна его магнитному моменту:

,

где вектор магнитного момента связан с направлением кругового тока правилом правого буравчика (см. рисунок) и перпендикулярен его плоскости.

Отметим, что магнитное поле кругового тока в целом имеет сложную конфигурацию и обладает осевой симметрией.

3. Магнитное поле элементарного контура.

Особый интерес представляет случай, когда контур с током плоский и его размеры достаточно малы. Такой контур с током называется элементарным.Примером элементарного контура являютсямолекулярные токи.Магнитное поле элементарного контура удобно описывать с помощью магнитного момента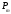, который определяется произведением токана площадь контура: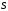

.

Магнитный момент является вектором . Векторперпендикулярен плоскости контура и его направление связано с направлением тока в контуре правилом правого буравчика (см. рисунок).

Магнитное поле элементарного контура подобно электрическому полю диполя (см. рисунок). Используя аналогично можно записать:

,

где .

Модуль вектора равен:.

4. Ток течет по длинному проводнику, имеющему форму желобас поперечным сечением в форме тонкой дуги окружности радиусом(см. рисунок). Определить индукцию магнитного поля в точках на оси желоба.

Магнитное поле на оси желоба можно представить как сумму полей элементарных линейных токов, результирующая которой направлена вдоль оси (см. рисунок).

Проекция:

где,.

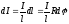Интегрируя по углу с учетом симметрии находим:

, где.

В частном случае тонкостенного полуцилиндра :

,

а на оси тонкостенной трубы .