§2. Примеры приведения матриц к жордановой форме

1.. Корни характеристического уравнения:_{1, 2, 3}= 1..

Собственные векторы Апо λ = 1, т.е. ядроА₁:

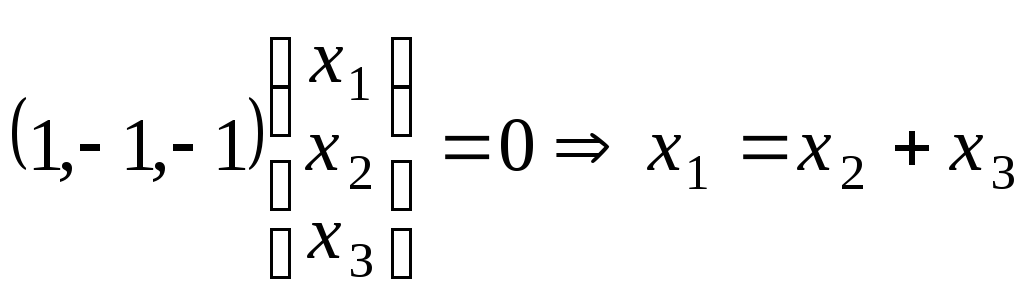, значит базисN(А₁):.

Образ оператора А₁ М(А₁) находим из соотношений:

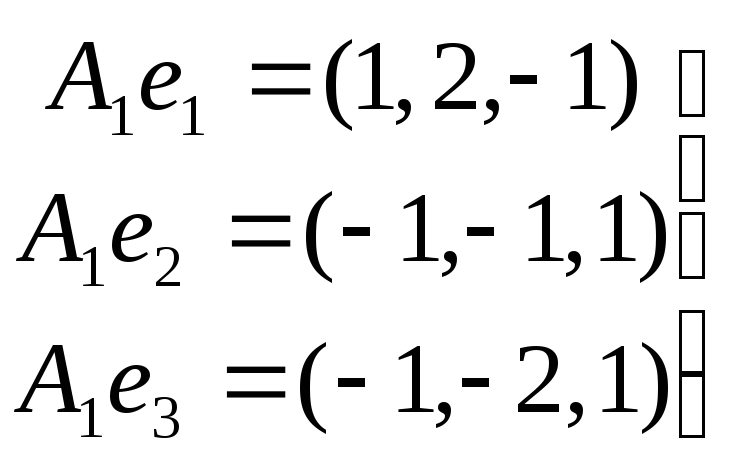; базисМ(А₁)f₃(1, 2, –1), и т.к.f₃= 2f₁–f₂, тоf₃ℒ(f₁,f₂).

Тогда: базисом будет вектор; вектором, дополняющим базисдо базисабудет любой из векторов, например вектор; а базисдополнить до базисанечем, т.к..

Прообраз А₁у= (1, 2, –1)у₁–у₂–у₃= 1 , например (1, 0, 0).

Кстати: система А₁у= (1, 0, 0) решений не имеет, т.е. прообраза второго слоя для вектора (1, 2, –1) нет.

Следовательно, жорданов базис оператора А:.

И, окончательно, имеем жорданову форму матрицы оператора А:.

2. Найти нормальную жорданову форму матрицы линейного оператора А = и базис, в котором матрица оператора имеет жорданову форму.

Δ. Для матрицы линейного оператора А=составим и решим характеристическое уравнение: det(AE) = 0 .

Получим:

=.

Тогда: = 0 и, следовательно,_{1, 2}= –1;_{3, 4}= 1.

a) Рассмотрим операторА_-1 =АE =А+E =. Ищем собственные векторы оператораАпри=1, т. е. ядро оператораА_-1. Для этого решим систему четырех линейных однородных уравнений с матрицейА_-1. Из третьего и четвертого уравнений системы видно, что. Тогда можно легко установить, что. Векторf₁(1, 1, 0, 0)единственный собственный вектор оператораА, соответствующий собственному значению=1 и образует базис ядра оператораА_–1. Далее ищем базис образа оператораА_–1:

.

Отметив, что для векторов f₂,f₃,f₄существует соотношение:f₃ +f₄ –f₂ = (0, 0, 0, 1), находим базис образа оператораА_–1:

{₁ (1, 1, 0, 0),₂ (0, –1, 1, 1),₃ (0, 0, 0, 1).

Отметив, что векторы f₁ и совпадают, делаем вывод о том, что этот вектор образует базис пересечения образа и ядра оператораА_-1.

Кратность корня λ = 1 равна двум, а собственный вектор, соответствующий этому собственному значению, только один. Поэтому, полагаемg₁ равным вектору, а еще один вектор жорданового базиса ищем, как прообраз первого слоя для. Решаем неоднородную систему линейных уравненийи находим второй векторg₂(1, 3/4, 0, 0) жорданового базиса, соответствующего собственному значению=1 кратности два. При этом, что характерно, у векторанет прообраза второго слоя, ибо системас расширенной матрицей

решений не имеет. Это и не случайно, потому что собственному значению =1 кратности 2 должно соответствует два вектора жорданового базиса оператораА:

g₁(1, 1, 0, 0);g₂(1, 3/4, 0, 0).

При этом отметим, что:

.

б) Теперь рассмотрим собственное значение = 1 и, соответственно, операторА₁=А+Е:

.

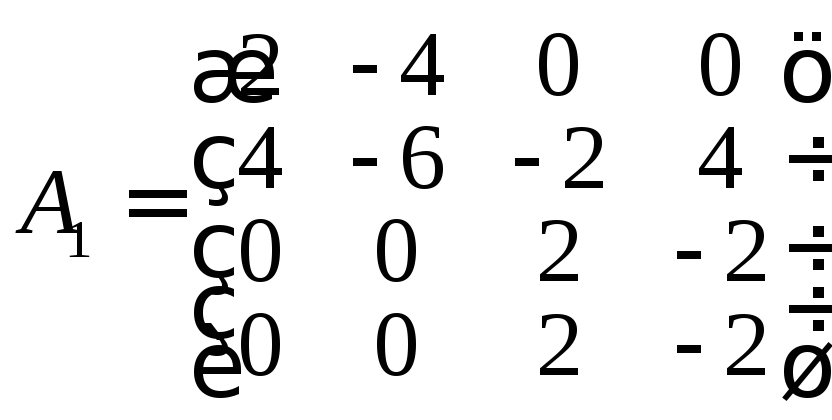Найдем ядро этого оператора, т.е. собственные векторы оператора Апри λ = 1.

.

Вектор f₁ (1, 1, 1, 1) образует базис ядра оператораА₁ и является единственным собственным вектором оператораА, отвечающим собственному значению= 1 .

Ищем базис образа М(А₁) оператораА₁ .

.

Отмечая, что f₁ =f₂ +f₃ +f₄, заключаем: базисом пересечения ядра и образа оператораA₁является векторf₁.

Так как собственный вектор только один, а собственное значение имеет кратность 2, требуется найти еще один вектор жорданового базиса. Поэтому полагаем g₃ равным вектору ₁(1, 1, 1, 1), а еще один вектор жорданового базиса ищем как прообраз первого слоя для ₁(1, 1, 1, 1). Для этого решаем неоднородную систему линейных уравнений A₁g₄ = ₁ и находим вектор g₄(0, 1/2, 0, 1/2) жорданового базиса, соответствующего собственному значению  = 1 кратности два. При этом у вектора ₁(1, 1, 1, 1) нет прообраза второго слоя, ибо система A₁y = g₄ с расширенной матрицей решений не имеет. И вновь это не случайно, потому что собственному значению = 1 кратности 2 должно соответствовать два вектора жорданового базиса, а они уже найдены:

g₃(1, 1, 1, 1);g₄(0, 1/2, 0, 1/2).

При этом отметим, что: Ag₃=g₁,Ag₄ =g₃ +g₄. Для оператораАнайден жорданов базис:. При этомА_G=. ▲

3.; det(AE) = 0_{1, 2}= 1;_{3, 4}= 2.

Δa) Рассмотрим операторА₁:А₁-E=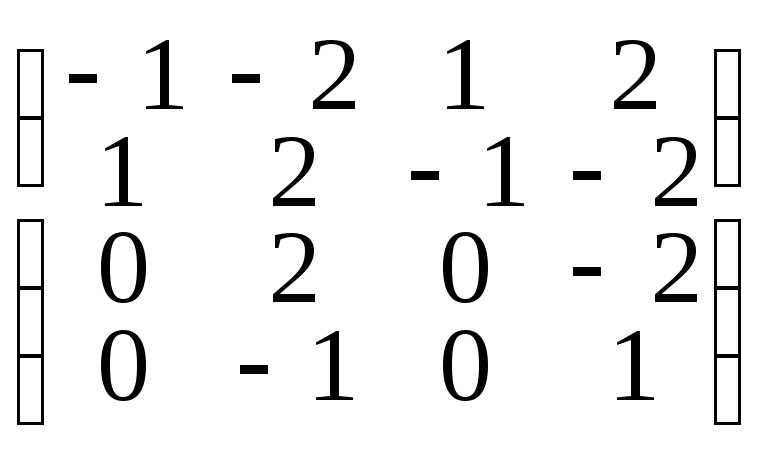. Ищем собственные векторы оператораАпри= 1, т.е. ядро оператораА₁.

. Векторы {f₁,f₂} образуют базисN(A₁).

Далее ищем базис.

Так как векторы f₁,f₂,f₃,f₄– линейно независимы, то, а векторы дополняющие базисдо базиса– векторы:

Кратность корня λ = 1 равна двум, поэтому имеем уже два вектора жорданового базиса А:

g₁(1, 0, 1, 0);g₂(0, 1, 0, 1).

б)Рассмотрим оператор А₂=А-2Е: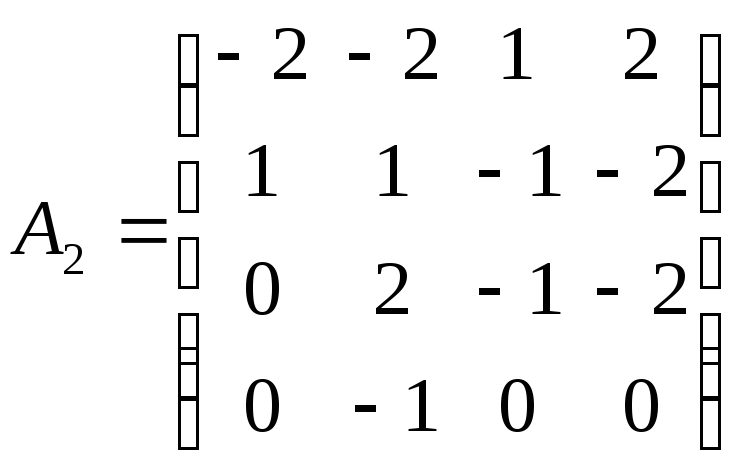, и найдем ядро оператораА₂т.е. собственные вектораАпри λ = 2.. Векторf₁(0, 0, –2, 1), являющийся решением этой системы является одновременно и базисом ядра.

Ищем базис образа оператора А₂ – М(А₂) .

.

Тогда, вектор (0, 0, –2, 1) это вектор жорданового базиса, а второй вектор – прообраз вектора (0, 0, –2, 1), если он есть. Система для его нахождения: А₂у= (0, 0, –2, 1).

Решаем систему А₂у= (0, 0, –2, 1), для нахождения прообраза 1^-гослоя вектора (0, 0, –2, 1) Получаем:.

Решением системы является, например, вектор (1, –1, 0, 0).

Тогда g₃(0, 0, –2, 1);g₄(1, ­1, 0, 0).

Для оператора Анайден жорданов базис:.

При этом 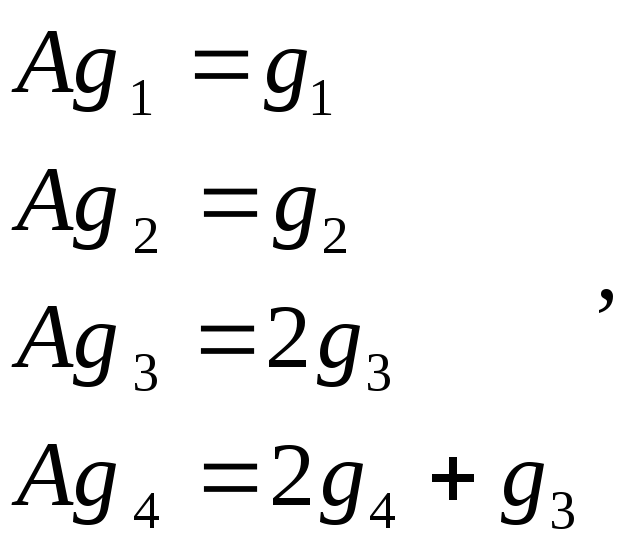т.е. жорданова форма оператораА:. ▲.