§15. Дифференциальные операции 1го порядка

1. Для векторного поляA_iобразуем градиент векторного поля, а затем получившийся тензор свернем по индексамi,j:.

Как известно, такая величина в векторном анализе называется дивергенцией векторного поля А( divA ). Подобным образом можно получить дивергенцию тензорного поля любого ранга, выше нулевого.

Результирующее тензорное поле имеет ранг на единицу меньший, чем исходное поле.

Для тензорного поля ранга r можно получитьrразличных тензорных полей (r – 1)^горанга типа «дивергенции» в зависимости от того, какой из индексов исходного поля сворачивается с индексом дифференцирования:.

2. В векторном анализе известна такая дифференциальная операция, как rotA=A. В тензорном представлении. Операторомможно действовать на тензор любого ранга выше нулевого и затем сворачивать индексlс одним из индексов этого тензора. Результирующее тензорное поле имеет тот же ранг, что и исходное.

Для тензорного поля ранга rможно получитьrразличных тензорных полейr^горанга типа «ротор» в зависимости от того с каким из индексов исходного поля сворачивать индексl.

.

3. Схематически операции градиента, дивергенции и ротора тензорного поля произвольного ранга можно задать следующим образом:

(gradT…)_i = ,

(divT…_i…) = ,

(rotT…_l…) =.

§16. Дифференциальные операции 2го порядка

1. Для скалярной функции φ:, и такая величина называется лапласианом функции.

Аналогично можно ввести лапласиан произвольного тензора ранга rи получить тензорное поле того же ранга:

Рассмотрим divrotA, гдеА– произвольное векторное поле:

Div rotA =

.

Равенство подчеркнутых выражений позволяет заключить, что divrotA= 0 для любого векторного поляА.

Аналогичное тождество имеет место для тензорного поля любого ранга (кроме нулевого): .

3. Проверим справедливость тождества: rot rot= grad divΔ.

◀ (rot rotA)_i =

(divA)  (A)_i = (grad divA)_i  (A)_i = (grad divA  A)_i ▶

Аналогичное тождество можно записать и для произвольного тензорного поля.

§17. Интегральные формулы тензорного анализа

1. В векторном анализе поток векторного полячерез поверхностьSопределяется как:(здесь– орт нормали к поверхностиS). При этом поток векторного поля это скаляр.

Аналогично можно определить поток тензорного поля ранга rчерез поверхностьS, как.

При этом поток тензорного поля ранга r через поверхностьSэто тензор (r– 1)^горанга (покажите, что поток это тензор). Всего существуетrразличных полей ранга (r– 1)типа «поток» в зависимости от того по какому индексу тензораТидет свертка.

2. Для векторных полей известна формула Гаусса-Остроградского:

.

Для тензорных полей существует rформул типа «Гаусса-Остроградского»

(справа и слева немой индекс должен быть один и тот же)

3. Формула Стокса для векторного поля имеет вид.

Та же формула в тензорной записи выглядит так: .

Формула Стокса может быть записана и для тензорных полей ранга r:

.

Всего может быть записано rформул типа «Стокса».

§18. Тензоры (задачи)

1. Показать, что произведение скаляра на тензор 2-го ранга является тензором 2-го ранга.

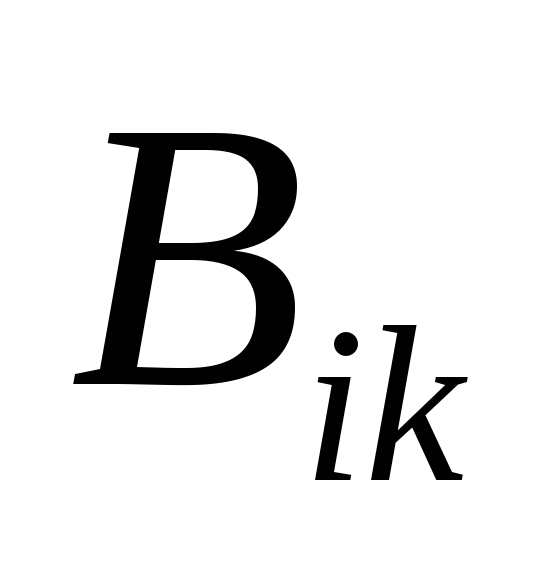2. Показать, что величина (где- тензор 3-го ранга,– тензор 2-го ранга) является вектором.

3. Доказать инвариантность свойств антисимметрии антисимметричного тензора 2-го ранга .

4. Показать, что произведение тензоров 3-го ранга и 2-го ранга является тензором 5-го ранга.

5. Компоненты тензора Т_ikв некотором ортонормированном базисеобразуют матрицуи, в том же базисе, векторВимеет координаты (1,2,3).

а) Разложить тензор Т_ikв сумму симметричногоS_ikи антисимметричноготензоров. б) Найти:

6. Пользуясь аппаратом тензорной алгебры, проверить тождества:

7. Записать в векторной форме выражение:

8. Пользуясь аппаратом тензорной алгебры, проверить тождества:

9. Пользуясь аппаратом тензорной алгебры, вычислить:

(радиус – вектор – , (постоянный вектор –))

10) Найти дивергенции и роторы следующих векторов:.

(радиус – вектор – , (постоянный вектор –а,b))

11) Вычислить интеграл , гдеa,c– постоянные вектора,n(r) – орт нормали к поверхностиS, которая ограничивает объемV.