§12. Связь тензоров 2го ранга с матрицей линейного оператора и с определителями

Пусть в Е_nзадан линейный операторАс матрицей (а_ij). Тогда:y_i=a_ijx_j(в базисее_i). Рассмотрим вЕ_nбазис {e_i}:y_i=a_ijx_j p_iiy_i =a_ijp_jjx_j . Умножим обе части равенства наp_ik.p_iip_iky_i =a_ijp_jjp_ikx_j _iky_i=a_ijp_jjp_ikx_j y_k=p_ikp_jja_ijx_j. С другой стороны:y_i=a_ijx_j, т.е.a_ij =p_iip_jja_ij.

Таким образом, элементы матрицы линейного оператора образуют тензор 2^горанга.

Наоборот всякий тензор 2^горанга можно истолковать как матрицу линейного оператора.

Поэтому теория тензоров 2^горанга непосредственно связана с теорией линейных операторов и с теорией матриц.

Это дает возможность выявить связь тензоров 2^горанга с определителями и т.д.

Теперь: пусть _ik– произвольный тензор 2^горанга. Построим тензор 3^горанга_abcпо правилу:_abc=_ikl_ia_kb_lc. Тогда_bac=_ikl_ib_ka_lc_kil_kb_ia_lc=_kil_ia_kb_lc= =_ikl_ia_kb_lc= –_abc. Следовательно абсолютно антисимметричный тензор 3^горанга всегда можно представить в виде:_abc=_abc, где φ – скаляр. Т.е. каждому тензору 2^горанга φ_ikможно поставить в соответствие скаляр φ такой, что:

_ikl_iа_kb_lc = _abc (*)

Оказывается, что этот скаляр равен определителю, составленному из компонент φ_ik:, в этом легко убедиться непосредственным вычислением, например, зафиксировав в (*) говорящие индексы (скажема= 1,b= 2,c = 3) и выполнив суммирование по немым индексамi,k,l:₁₂₃ =_ikl_i1_k2_l3 = …

В этой же идеологии нетрудно ввести понятия тензора обратного к данному тензору 2^горанга (Если, то тензоробратный к тензору_ik), и получить условия обратимости тензора 2^горанга.

Можно сформулировать (а для симметричного тензора и всегда решить) задачу о приведении тензора 2^горанга к главным осям. Эта задача равносильна задаче построения собственного базиса для линейного оператора.

§13.Тензорные поля

В физических приложениях, как правило, встречаются тензоры, компоненты которых представляют собой функции координат (x₁,x₂,x₃) точек пространства.

Def: Тензорным полемr^горанга(x₁,x₂,x₃) является совокупность 3^rфункций, которые в любой данной точке пространства образуют тензорr^горанга.

Изучение тензорных полей и составляет предмет тензорного анализа.

В дальнейшем речь будет идти о непрерывных тензорных полях , (где– радиус-вектор точки с координатамиx₁,x₂,x₃). Это значит, что абсолютные величины разностеймогут быть сделаны сколь угодно малыми, при достаточно малых.

§14. Дифференцирование тензорного поля по координатам точки пространства

Пусть – тензорное полеr^горанга. Каждую из 3^rкомпонент этого поля продифференцируем по каждой из трех координатx₁,x₂,x₃. Получим совокупность 3^r+1функций вида(j= 1, 2, 3).

Тº.Если– тензорное поле рангаr, тобудет тензорным полем ранга (r+ 1).

◀ Отметим что, если x_i=p_iiто=p_ii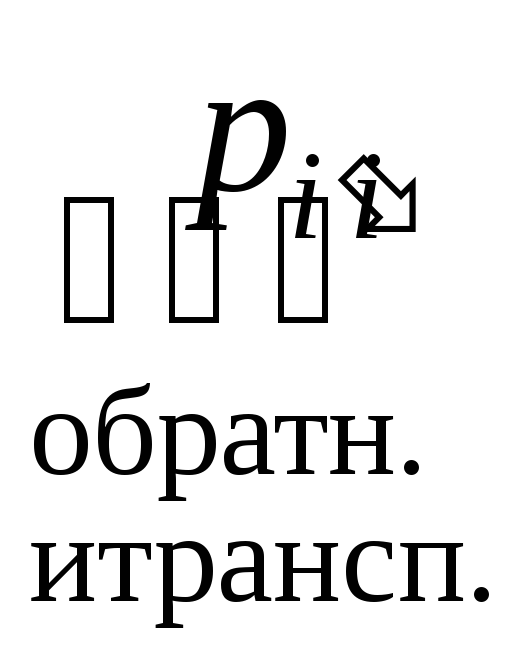 =, и следовательно

▶

Итак, дифференцирование тензорного поля по координатам повышает ранг тензорного поля на единицу.

В частности, применение этой операции к скалярному полю φ порождает векторное поле , которое называется градиентом скалярного поля.

По аналогии с градиентом скалярного поля, тензорное поле (j= 1, 2, 3) называют градиентом тензорного полярангаr.