
- •Министерство образования и науки украины
- •§2. Специальное представление полуторалинейных форм
- •Сопряженные и самосопряженные операторы в унитарном пространстве §1. Сопряженный оператор
- •Свойства сопряженных операторов.
- •§2. Эрмитовы (самосопряженные) операторы
- •§3. Норма оператора
- •4|Re(Ах,у)|4| Re(Ах,у)|.
- •§4. Еще о свойствах эрмитового оператора
- •§5. Спектральное разложение эрмитового оператора. Теорема Гамильтона – Кэли
- •§6. Положительные операторы. Корень m-й степени из оператора
- •Эрмитовы Формы §1. Полуторалинейные эрмитовы формы
- •§2. Квадратичные формы в унитарном пространстве
- •Унитарные и нормальные операторы §1. Унитарные операторы
- •§2. Нормальные операторы
- •Канонический вид линейного оператора §1. Нормальная жорданова форма
- •§2. Примеры приведения матриц к жордановой форме
- •Линейные операторы в евклидовом пространстве §1. Общие замечания и напоминания
- •§2. Ортогональные операторы
- •Билинейные и квадратичные формы
- •§3. Экстремальные свойства квадратичной формы
- •Элементы теории групп §1. Понятие группы. Подгруппы
- •§2. Примеры групп
- •§3. Еще определения
- •§4. Некоторые свойства групп
- •§5. Изоморфизм групп
- •§6. Смежные классы. Нормальные делители
- •§7. Свойства смежных классов (сформулированы для левых, но справедливы и для правых)
- •§8. Примеры построения смежных классов
- •§9. Гомоморфизмы. Фактор-группа
- •§10. Две теоремы о гомоморфизмах
- •§11. Группы линейных преобразований
- •§12. Группа Лоренца
- •§13. Линейные представления групп. Терминология
- •§14. Приводимые и неприводимые представления
- •§15. Характеры
- •§16. Примеры представлений групп
- •Элементы теории тензоров
- •§1. Определитель Грамма
- •§2. Взаимные базисы. Ковариантные и контравариантные координаты векторов
- •Примеры.
- •§3. Преобразование базиса и координат
- •Пример: Пусть е1(1, 1, 0) е1(1, 0, 0)
- •§4. Понятие тензора
- •§5. Примеры тензоров
- •§6. Основные операции над тензорами
- •§7.Афинные ортогональные тензоры
- •§8. Операции над аффинными ортогональными тензорами
- •§9 Признак тензорности величины
- •§10 Еще раз о свойствах симметрии тензоров
- •§11. Псевдотензоры
- •§12. Связь тензоров 2го ранга с матрицей линейного оператора и с определителями
- •§13.Тензорные поля
- •§14. Дифференцирование тензорного поля по координатам точки пространства
- •§15. Дифференциальные операции 1го порядка
- •§16. Дифференциальные операции 2го порядка
- •§17. Интегральные формулы тензорного анализа
- •§18. Тензоры (задачи)
- •Экзаменационные вопросы по курсу высшей алгебры
- •Часть II.
- •Экзаменационные задачи по курсу "высшая алгебра". Часть II
Экзаменационные задачи по курсу "высшая алгебра". Часть II
Найти матрицу A*оператора сопряженного к линейному операторуAпо заданной матрице оператораAи матрице Грамма Г:
а)
![]() :
:![]() ;
б)
;
б) :
: .
.
Найти матрицу A*оператора сопряженного к линейному операторуAпо заданной матрице оператораAи скалярному произведению:
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ;
;
в)
![]() ,
,![]() .
.
Оператор
 переводит векторыa1,a2, в векторыb1,b2,
соответственно. Найти оператор
A*,
если базис в котором заданы
переводит векторыa1,a2, в векторыb1,b2,
соответственно. Найти оператор
A*,
если базис в котором заданы ,
, - ортонормирован:
- ортонормирован:
а)
![]() ;
;![]() ;
;
б)
![]() ;
;![]() .
.
Оператор
 задан матрицей в базисеf1,f2, гдеf1=e1+e2,f2=e1–ie2. НайтиA*в том же базисе.
задан матрицей в базисеf1,f2, гдеf1=e1+e2,f2=e1–ie2. НайтиA*в том же базисе.
Оператор
 задан матрицей в базисе
задан матрицей в базисе ,
где
,
где .
Найти
.
Найти в том же базисе.
в том же базисе.
В евклидовом пространстве полиномов степени не выше 2 со скалярным произведением
 (здесь
(здесь и
и коэффициенты полиномовpиqпри
коэффициенты полиномовpиqпри )
задан оператор
)
задан оператор .
Найти
.
Найти в следующих базисах:
в следующих базисах:
а)
![]() ;
б)
;
б)![]() .
.
В евклидовом пространстве полиномов степени не выше 2 со скалярным произведением
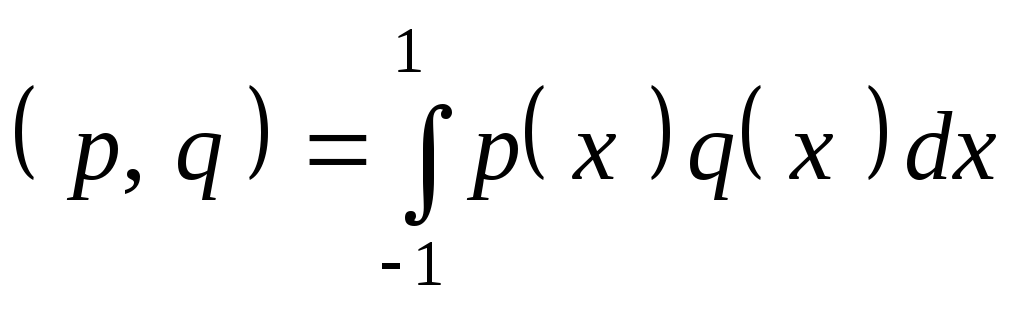 задан оператор
задан оператор .
Найти
.
Найти в следующих базисах: а)
в следующих базисах: а) ;
б)
;
б) .
.
Пусть в унитарном пространстве дифференцируемых и периодичных с периодом
 функций, скалярное произведение имеет
вид:
функций, скалярное произведение имеет
вид: .
Доказать, что оператор
.
Доказать, что оператор - эрмитов.
- эрмитов.
Установить является ли оператор
 самосопряженным, если оператор
самосопряженным, если оператор задан матрицей в базисе с матрицей
Грамма
задан матрицей в базисе с матрицей
Грамма :
:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() .
.
Оператор задан матрицей
 в базисе с матрицей Грамма
в базисе с матрицей Грамма .
Будет ли оператор
.
Будет ли оператор - эрмитовым?
- эрмитовым?
Установить, является ли ортогональным оператор
 ,
действующий на векторы ортонормированного
базиса по формулам:
,
действующий на векторы ортонормированного
базиса по формулам:
а)
![]() ;
б)
;
б)![]() .
.
Установить, является ли оператор
 унитарным, если
унитарным, если действует на векторы ортонормированного
базиса по формулам:
действует на векторы ортонормированного
базиса по формулам:
![]() .
.
Установить, является ли ортогональным линейный оператор, заданный в ортонормированном базисе матрицей:
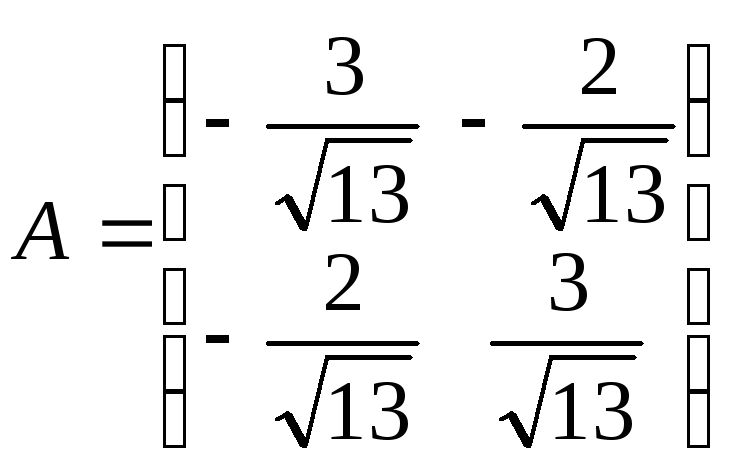 .
.
Установить, является ли ортогональным оператор
 ,
если он задан матрицей в базисе
,
если он задан матрицей в базисе ,
а векторы
,
а векторы выражаются через векторы ортонормированного
базиса
выражаются через векторы ортонормированного
базиса :
:
а)
![]() ;
;
б)
![]() ;
;
в)
 .
.
Построить собственный ортонормированный базис самосопряженного оператора, который, в некотором ортонормированном базисе, задан матрицей:
а)
![]() ;
б)
;
б)![]() .
.
Построить собственный ортонормированный базис эрмитового оператора, который, в некотором ортонормированном базисе, задан матрицей:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Построить собственный ортонормированный базис унитарного оператора, заданного в некотором ортонормированном базисе матрицей:
а)
![]() ;
б)
;
б) ;
в)
;
в)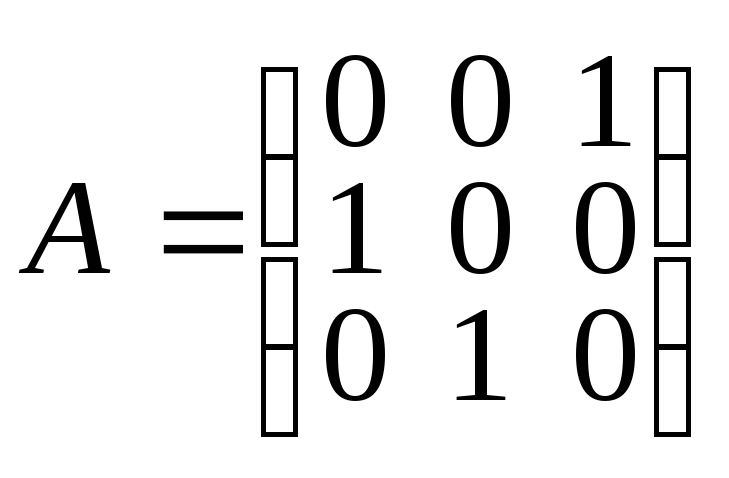 .
.
Привести матрицу
 к диагональному виду.
к диагональному виду.Найти:
а)
![]() ,
,![]() ;
б)
;
б)![]() ,
,![]() ;
в)
;
в)![]() ,
,![]() ;
;
г)
![]() ,
,![]() ;
д)
;
д)![]() ,
,![]() ;
е)
;
е)![]() ,
,![]() .
.
Установить, являются ли следующие квадратичные формы положительно определенными:
а)
![]() ;
;
б)
![]() .
.
Установить, при каких
 следующие квадратичные формы являются
положительно определенными:
следующие квадратичные формы являются
положительно определенными:
а)
![]() ;
;
б)
![]() .
.
Найти ортонормированный базис, в котором следующие квадратичные формы (заданные тоже в ортонормированном базисе) имеют диагональный вид:
а)
![]() ;
;
б)
![]() .
.
Привести следующие квадратичные формы к нормальному виду:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
С помощью одного преобразования привести пару форм к каноническому виду:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Найти базис, взаимный к данному:
а)
![]() ;
;
б)
![]() .
.
Вектор
 задан своими координатами в том же
базисе, в котором заданы координаты
векторов двух взаимных базисов:
задан своими координатами в том же
базисе, в котором заданы координаты
векторов двух взаимных базисов:
 и
и .
Найти ковариантные и контравариантные
координаты вектора
.
Найти ковариантные и контравариантные
координаты вектора .
.
Доказать инвариантность свойства антисимметрии тензора второго ранга
 .
.
Используя тензорную форму записи проверить тождества:
а)
![]() ;
;
б)
![]() .
.
Используя тензорную форму записи, вычислить:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ; г)
; г)![]() ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з)![]() .
.
(здесь
![]() - постоянные векторы,
- постоянные векторы,![]() - радиус вектор).
- радиус вектор).
Используя тензорную форму записи, доказать тождества:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
(здесь
![]() - векторные поля,
- векторные поля,![]() - скалярное поле).
- скалярное поле).
Вычислить (используя интегральные теоремы тензорного исчисления)
 ,
где
,
где - постоянные векторы,
- постоянные векторы, - орт нормали к поверхности
- орт нормали к поверхности ,
которая ограничивает объем
,
которая ограничивает объем .
.
32. Найти результат действия перестановок:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
Возвести перестановки в степень:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
г)
;
г)![]() .
.
Найти перестановку, обратную перестановке:
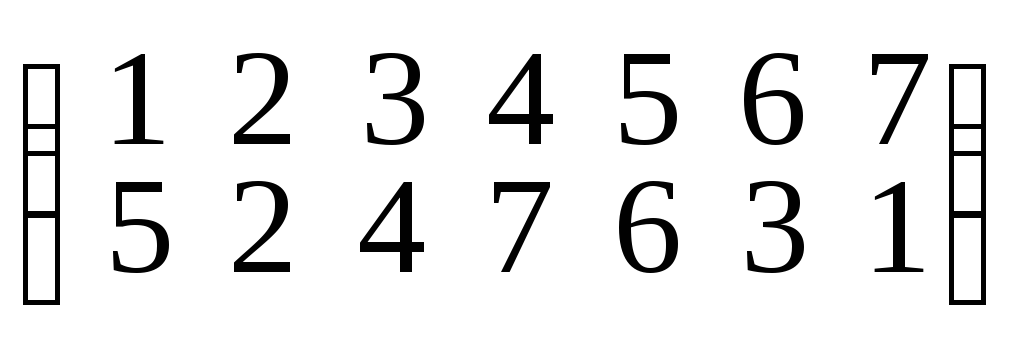 .
.Найти
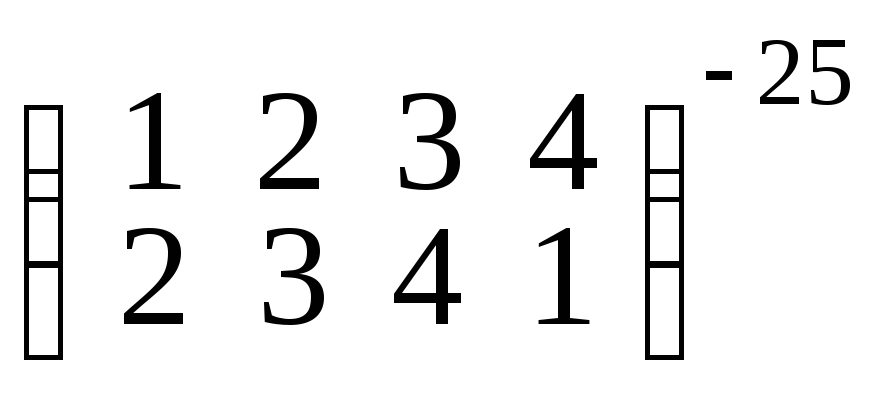 .
.
Найти:
а)
![]() ;
б)
;
б)![]()
Если
 группа перестановок
группа перестановок чисел, то найти все подгруппы
чисел, то найти все подгруппы .
.
Построить смежные классы к
 в
в ,
где
,
где и
и - группы корней 3-й и 6-йстепени из 1, соответственно.
- группы корней 3-й и 6-йстепени из 1, соответственно.
Построить смежные классы к
 в
в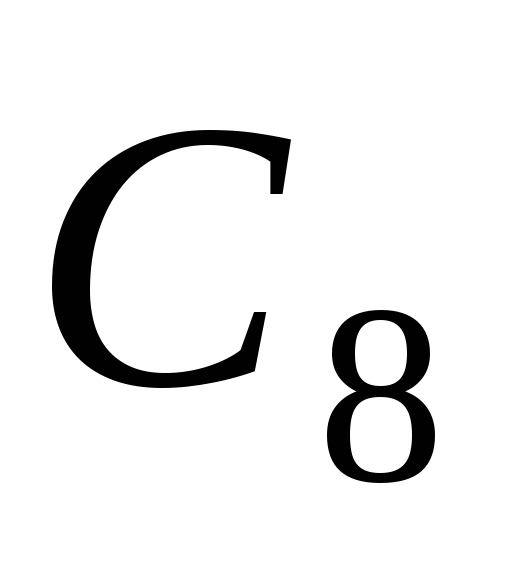 ,
где
,
где и
и - группы корней 4-й и 8-йстепени из 1, соответственно.
- группы корней 4-й и 8-йстепени из 1, соответственно.
Доказать, что
 - нормальный делитель группы
- нормальный делитель группы ,
где
,
где и
и - группы корней 3-й и 6-йстепени из 1, соответственно.
- группы корней 3-й и 6-йстепени из 1, соответственно.
Доказать, что
 - нормальный делитель группы
- нормальный делитель группы ,
где
,
где и
и - группы корней 4-й и 8-йстепени из 1, соответственно.
- группы корней 4-й и 8-йстепени из 1, соответственно.
Найти все гомоморфизмы
 в
в ,
где
,
где группа корнейn-йстепени из 1.
группа корнейn-йстепени из 1.
Найти фактор-группу
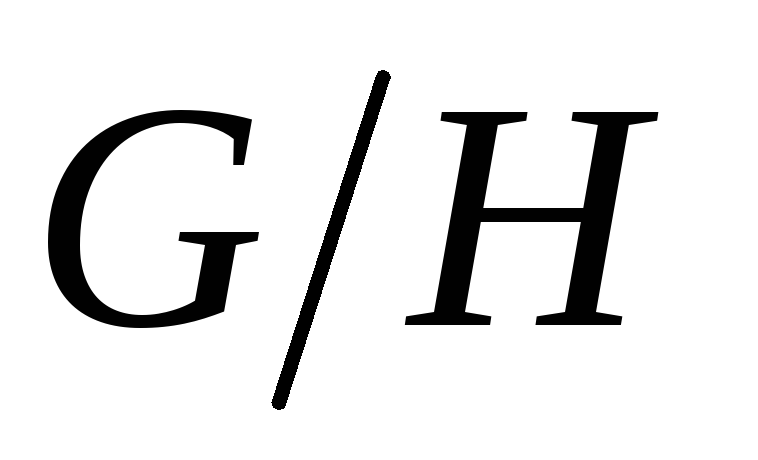 ,
если:
,
если:
а)
![]() - группа целых чисел,
- группа целых чисел,![]() - подгруппа чисел, кратных заданному
целому
- подгруппа чисел, кратных заданному
целому
числу
![]() ;
;
б)
![]() - группа всех вещественных чисел по
сложению,
- группа всех вещественных чисел по
сложению,![]() - подгруппа целых
- подгруппа целых
чисел;
в)
![]() - группа всех комплексных чисел по
сложению,
- группа всех комплексных чисел по
сложению,![]() - группа веществен-
- группа веществен-
ных чисел тоже по сложению;
г)
![]() - группа ненулевых комплексных чисел
по умножению,
- группа ненулевых комплексных чисел
по умножению,![]() - группа
- группа
положительных вещественных чисел по умножению;
д)
![]() - группа ненулевых комплексных чисел
по умножению,
- группа ненулевых комплексных чисел
по умножению,![]() - подгруппа
- подгруппа
чисел по модулю равных 1.
43. Найти нормальную жорданову форму матрицы:
а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
;
д)  ;
е)
;
е)  ;
ж)
;
ж)  ;
з)
;
з)  .
.
