Канонический вид линейного оператора §1. Нормальная жорданова форма

Пусть А– линейный оператор, действующий в комплексном векторном пространствеV. Если вVсуществует базис {e_k} из собственных векторов оператораА, то в этом базисе матрица оператораАимеет диагональный вид, где λ – соответствующие собственные значения оператораА.

Так будет, например, в том случае, когда характеристичное уравнение оператора А: det(A–Е) = 0 имеетnпопарно различных корней.

Однако это далеко не всегда так. Например, оператор Ас матрицейА=имеет характеристическое уравнение:() = (2)²= 0. Это уравнение имеет кратный корень λ = 2 и этому корню соответствует лишь один собственный вектор (1, 0) (или ему коллинеарные). И матрица оператораАни в каком базисе не приводится к диагональному виду.

Поэтому возникает вопрос, о каком-то другом, достаточно простом виде, к которому можно привести матрицу всякого линейного оператора.

В комплексном пространстве таким «простейшим», каноническим видом принято считать так называемую жорданову форму матрицы.

Def: Жордановой клеткойG_k(λ) называется квадратная матрицаk-го порядка вида:

.

Порядок жордановой клетки может быть любым. В частности, если k = 1, то клетка имеет простейший вид : (λ)

Def: Жордановой матрицей называется матрица вида: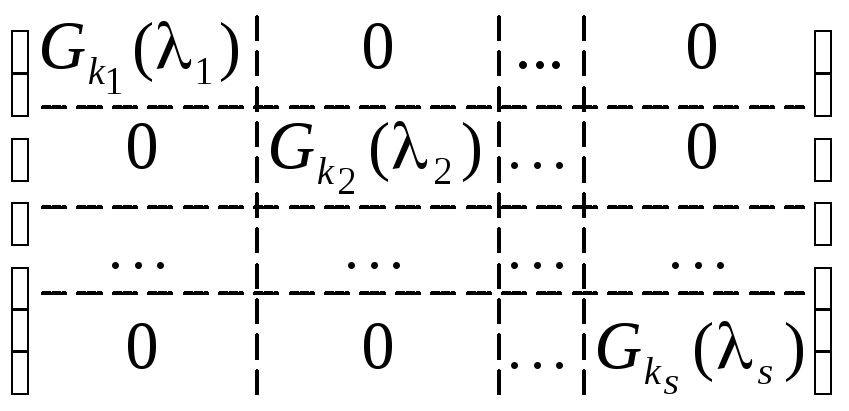. ЗдесьG_k(λ) – жордановы клетки.

В частности, если оператор Аимеет матрицу, то нормальная жорданова форма матрицы оператора состоит из двух жордановых клеток. Нетрудно заметить, чтои β – соответственные значения оператораА. И, кроме того:

Ае₁=е₁; Ае₂=е₂+е₁;Ае₃=е₃+е₂;Ае₄=е₄;Ае₅=е₅+е₄.

Тº. Произвольный линейный операторАв комплексном пространствеVимеет базис

, в котором матрица оператораАимеет жорданову форму.

Доказательство теоремы довольно громоздко и мы его не приводим. Построение базиса и приведение матрицы оператора к жордановой форме продемонстрируем на примерах.

Схема нахождения нормальной жордановой формы матрицы оператора и построения жорданова базиса.

Схема построена на построении циклических инвариантных подпространств, которые были рассмотрены в первой части нашего курса.

1. Нахождение собственных векторов и собственных значений оператора А. Если количество собственных линейно независимых векторов равно размерности пространства, то в указанном базисе матрица оператора имеет диагональный вид;

2. Если для кратного собственного значения кратности kколичество линейно независимых собственных векторов также равноk, то в этом базисе матрица также имеет диагональный вид;

3. Для кратных собственных значений таких, что количество линейно независимых собственных векторов меньше кратности корня, поиск базисных векторов производится так:

а) находим собственные векторы А, т.е. базисN(A_) ядра оператораА_=А–Е;

б) находим М(А_) – образ оператораА_и его базис;

в) ищем базис М(А_) ∩N(А_) ;

г) для каждого вектора М(А_) ∩N(А_) находим прообраз 1-го слоятакой, чтоА_, прообраз 2-го слоятакой, чтоА_, и т.д. до тех пор пока они есть.

Жорданов базис формируется следующим образом:

а) первыми в базис попадают базисные векторы ядра оператора А_вместе со своими прообразамих₁,y₁₁,y₁₂, …,х₂,y₂₁,y₂₂,… …,х_р,y_p1,y_p2….

б) затем в базис включаются векторы х_p+1,х_p+2, …,х_l, дополняющие базисМ(А_) ∩N(А_) до базиса ядра оператораА_ , если такие есть.

* Замечание: Процесс проводится для каждого значения  до тех пор пока количество векторов, включенных в базис не станет равным кратности k собственного значения .

Искомый базис: х₁,y₁₁,y₁₂, …,х₂,y₂₁,y₂₂,… …,х_р,y_p1,y_p2….,х_p+1,х_p+2, …,х_l.

( Всегоkвекторов).