Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

Глава 10

Квантовые алгоритмы

DRAFTМы начали эту книгу со старинных алгоритмов для сложения и умножения чисел и с классической трудной задачи (разложение на множители, factoring). В этой главе –– последней главе книги –– всё будет наоборот: мы расскажем о недавно придуманном алгоритме, и это будет быстрый алгоритм разложения на множители!

Конечно, тут есть тонкость: это будет алгоритм для квантового компьютера.

Поведение элементарных частиц и других микроскопических объектов описывается красивой, но загадочной теорией –– квантовой механикой. В 1990-е годы было обнаружено, что законы квантовой механики открывают возможность для быстрых вычислений –– в том числе экспоненциально более быстрых. Как мы увидим, квантовые компьютеры (если они будут действовать так, как сейчас предполагается) смогут разлагать числа на множители за полиномиальное время. Пока такие компьютеры ещё не сделаны –– но когда и если они появятся, многое изменится, и не только в лучшую сторону. Например, современные системы защиты информации при передаче по интернету и в банках (большей частью используется RSA) утратят надёжность.

10.1. Кубиты, суперпозиция, измерения

В этом разделе мы кратко опишем основные принципы квантовой механики, на которых основано действие квантовых компьютеров.1

В обычных компьютерах два значения бита (нуль или единица) закодированы как низкое и высокое напряжение в проводниках схемы. Можно было бы кодировать их иначе –– например, атом водорода в основном состоянии (с малой энергией) может кодировать нуль, а в возбуждённом состоянии (с большой энергией) –– единицу.

Используя традиционные обозначения квантовой механики, мы записываем основное состояние (ground state) как j0i, а возбуждённое состояние (excited state) как j1i. С точки зрения классической физики, атом может находиться либо в одном состоянии, либо в другом. В квантовой

1Рассказывают, что знаменитый физик Ричард Фейнман как-то сказал: «Думаю, что можно смело утверждать, что квантовую механику не понимает никто». Так что вряд ли чтение этого раздела позволит вам в ней разобраться как следует –– но в конце книги мы указываем несколько источников для дальнейшего чтения. [Мы благодарим М. Н. Вялого за помощь в переводе этой главы. –– Прим. перев.]

механике –– как это ни странно на первый взгляд –– возможны и суперпозиции (superpositions) этих состояний: формальные линейные комбинации0j0i + 1j1i, где 0 и 1 –– любые комплексные числа, сумма квадратов модулей которых равна единице: j 0j2 + j 1j2 = 1. Например, возможно состоя-

называют амплитудами (amplitudes) состояний j0i и j1i соответственно. Напомним, что амплитуды могут быть комплексными, так что, скажем, мож-

мнимую единицу, i = p 1). Такого рода суперпозиции, 0j0i + 1j1i, описывают состояние элементарной ячейки для хранения информации (см. рисунок 10.1), называемой кубитом (qubit).

Рис. 10.1. Электрон в атоме водорода может находиться в основном и возбуждённом состояниях. В обозначениях Дирака, традиционно используемых в квантовой механике, их записывают как j0i и j1i. Но принцип суперпозиции (superposition principle) говорит нам, что на самом деле возможны и линейные комбинации (linear combinations) этих состояний: 0j0i + 1j1i. Говорят, что состояние 0j0i + 1j1i является суперпозицией базисных состояний j0i и j1i. Если бы 0 и 1 были неотрицательными числами, в сумме равными 1, то это можно было бы понимать так: электрон находится в состоянии 0 с вероятностью j 0i и в состоянии 1 с вероятностью j 1i. Однако 0 и 1 могут быть комплексными числами, и единице должна быть равна не их сумма, а сумма квадратов их модулей!

Выражаясь фигурально, можно сказать, что электрон в атоме ещё сам не решил, в каком состоянии он находится –– основном или возбуждённом, а числа 0 и 1 выражают его «предрасположенность» к тому и другому состоянию. Но понимать «предрасположенность» как вероятность нельзя: 0 и 1 могут быть отрицательными или вообще мнимыми. И как тогда её понимать, спрашивается? Это одно из самых загадочных мест в квантовой механике, к которому наша интуиция приспосабливается с трудом.

Продолжая метафору, можно сказать, что состояние электрона (суперпозиция основного и возбуждённого состояний) описывает его «внутренний мир». Этот «внутренний мир» нам недоступен, но мы можем выполнить измерение (measurement), см. рис. 10.2. Результатом измерения является нуль или единица. При этом вероятности появления нуля и единицы равны со-

Рис. 10.2. Измерение системы в состоянии суперпозиции переводит её в одно из базисных состояний, и вероятности их появления равны квадратам модулей амплитуд.

ответственно j 0j2 и j 1j2 (напомним, что как раз сумма квадратов модулей должна быть равна единице). Побочным (но неизбежным) результатом измерения является то, что система оказывается в измеренном состоянии: если измерение дало 0, то система находится после измерения в основном состоянии (j0i = 1 j0i + 0 j1i), а если 1 –– то в возбуждённом (j1i). Невозможность измерить состояние системы, не повлияв на него, –– другая странная особенность квантовой механики, не имеющая аналогов в классической физике.

Принцип суперпозиции применим не только к системам с двумя состояниями. На самом деле даже в нашем примере (электрон в атоме водорода) возможно несколько возбуждённых состояний, и можно рассмотреть систему с k базисными состояниями: основным и k 1 возбуждёнными. Обозначим их j0i, j1i, ‌, jk 1i. Произвольная суперпозиция такой системы записывается тогда как 0j0i + 1j1i + ‌ + k 1jk 1i, где j 0j2 + j 1j2 + ‌ + j k 1j2 = 1. Результатом измерения в такой системе будет число от 0 до k 1, и вероятность появления числа j равна j j j2. Как мы уже говорили, измерение меняет состояние системы, и её новое состояние определяется результатом измерения.

Для кодирования n битов можно было бы использовать систему с 2n базисными состояниями (скажем, достаточно возбуждённый атом водорода), но лучше использовать n кубитов.

Рассмотрим два кубита, представляющих собой состояния электронов в двух атомах водорода (в каждом атоме используются два состояния –– основное и возбуждённое). В классической физике два состояния для каждого атома дают всего четыре комбинации 00, 01, 10, 11 (сначала мы записываем состояние одного атома, а потом –– второго). Тем самым два атома можно использовать для хранения двух битов информации –– по одному на атом. В квантовой механике принцип суперпозиции позволяет рассмотреть линей-

j x j . Если измерение дало исход x = jk, то после измерения система окажется в чистом состоянии x: если, скажем, x = 10, то первый электрон будет в возбуждённом состоянии, а второй –– в основном.

Сцепленность

Пусть у нас есть два кубита. Первый находится в состоянии 0j0i + 1j1i, а второй –– в состоянии 0j0i + 1j1i. Каково состояние системы, состоящей из этих двух кубитов? Ответ: тензорное произведение указанных выше состояний, которое имеет вид

0 0j00i + 0 1j01i + 1 0j10i + 1 1j11i.

Можно ли для произвольного состояния системы из двух кубитов выделить состояния каждого из них, обратив эту процедуру? Не всегда. Говорят, что кубиты сцеплены (entangled), если их совместное состояние невозможно разложить в произведение индивидуальных состояний. Рассмотрим, на-

пример, состояние j i = 1 j00i + 1 j11i (одно из состояний Белла). Его p p

2 2

невозможно разложить в произведение состояний первого и второго кубитов (см. упражнение 10.1). Сцепленность (entanglement) –– главная загадка квантовой механики; именно на ней основана надежда на вычислительные возможности квантовых устройств.

Ещё одна интересная возможность –– это возможность частичного измерения (partial measurement). Мы можем измерить, скажем, только первый бит. Какова вероятность, что мы обнаружим его в состоянии 0? Такая же, как если бы мы измерили два бита сразу, то есть j 00j2 + j 01j2. Более сложный вопрос: в каком состоянии окажется система после такого измерения?

Квантовая механика отвечает на этот вопрос так: если результат измерения первого бита равен 0, то в суперпозиции останутся только члены с таким значением первого бита, а коэффициенты перед ними будут перенормированы: умножены на положительное число с тем расчётом, чтобы сумма квадратов снова стала равной единице. В нашем примере новым состоянием будет

00 01

j новоеi = p j00i + p j01i.

j 00j2 + j 01j2 j 00j2 + j 01j2

Теперь рассмотрим случай n атомов (в качестве n можно взять сравнительно небольшое число, скажем, n = 500). С классической точки зрения, такая система может хранить 500 битов информации. В квантовой механике её состояние представляет собой линейную комбинацию 2500 классических (базисных) состояний с комплексными коэффициентами:

X

x jxi

x2f0,1gn

Получается, что Природе нужно помнить 2500 комплексных чисел –– и это только для состояния 500 атомов водорода! Более того, эти числа надо не только помнить, но и менять, если состояние системы меняется со временем.

Число 2500 много больше числа элементарных частиц во всей Вселенной. Неужели Природа может хранить столько информации? И где? И это только для одной совсем небольшой системы. Как ни странно, именно так всё и происходит согласно квантовой механике.

Раз так, почему бы не обратить это себе на пользу и не использовать возможности Природы для вычислений? В этом и состоит основная идея квантовых компьютеров.

Реализовать её, однако, совсем не просто. Одна из трудностей: упомянутая сумма экспоненциального размера отражает «внутренний мир» системы, а в процессе измерения мы получаем всего лишь n битов информации. (Напомним, что вероятность получить в результате измерения слово x длины n равна j x j2, квадрату модуля соответствующего коэффициента, и после измерения система переходит в состояние jxi.)

Рис. 10.3. Квантовый алгоритм может взять n классических битов входа, сделать их состояниями n кубитов, затем произвести какие-то действия и получить в результате суперпозицию состояний с 2n коэффициентами, после чего в процессе измерения получить снова n классических битов (в соответствии с распределением вероятностей, задаваемым квадратами модулей коэффициентов). Каждое из действий с суперпозицией воздействует на экспоненциальное число коэффициентов –– и тем не менее с физической точки зрения остаётся всего лишь одним шагом.

суперпозиция

296 Глава 10. Квантовые алгоритмы

10.2. План действий

Квантовый алгоритм не будет похож на классические. Причина этого в необходимости всё время иметь в виду разницу между внутренним состоянием экспоненциального размера и доступной для наблюдения информацией (всего лишь n битов).

На входе и выходе квантового алгоритма мы имеем слова из n (классических) битов; работа с экспоненциальными объёмами информации, которую Природа для нас выполняет по законам квантовой механики, остаётся нена-

DRAFTно размеру входа, что, конечно, вовсе не обязательно.) Наконец, мы выполняем измерение и получаем на выходе некоторое n-битовое слово y с вероятностью j y j2.

блюдаемой.

Получив на вход слово из n битов, мы приводим систему в состояние jxi.

Затем выполняются какие-то операции (по законам квантовой механики), и

в результате наша система из n кубитов приходит в состояние P y jyi. (Мы

y

предполагаем для простоты, что число кубитов в квантовом компьютере рав-

То, что выходное слово алгоритма случайно, само по себе не страшно: с такой ситуацией мы уже встречались, говоря о вероятностных алгоритмах (скажем, алгоритме проверки простоты). Нужно только, чтобы слово y с большой вероятностью содержало в себе информацию о верном ответе. Тогда, повторив вычисление несколько раз, мы можем сделать вероятность ошибки пренебрежимо малой.

Обсудим теперь более подробно квантовую часть алгоритма разложения на множители. Как мы вскоре увидим, с помощью квантовых операций мы сможем искать некоторые закономерности в коэффициентах суперпозиции (периодичность), и информация об этих закономерностях поможет разложить число на множители. Но до этого мы должны будем преобразовать («распаковать») n классических битов входа в экспоненциальную сумму таким образом, чтобы эти закономерности в коэффициентах появились. После этого другие операции (и заключительное измерение) позволят их найти.

Всё это звучит более чем загадочно, но вскоре мы все эти шаги объясним. В разделе 10.3 мы описываем основной механизм, используемый в алгоритме –– квантовый вариант быстрого преобразования Фурье (FFT). Затем мы опишем закономерности, которые с его помощью можно найти, и сведём задачу разложения на множители к поиску таких закономерностей. Наконец, мы покажем, как на первой стадии преобразовать заданное нам число N в суперпозицию экспоненциального размера, в которой эти закономерности следует искать.

Вот схема алгоритма разложения N на множители с помощью квантового компьютера (выделенные курсивом термины будут объяснены дальше):

ff Разложение на множители сводится к нахождению нетривиального квадратного корня из единицы по модулю N.

ff Нахождение такого корня сводится к вычислению порядка случайного числа по модулю N.

ffПорядок числа по модулю N оказывается периодом некоторой периодической суперпозиции.

ffНаконец, периоды суперпозиций можно вычислять с помощью квантового преобразования Фурье.

Мы начнём с последнего шага.

10.3. Квантовое преобразование Фурье

DRAFTзуют базис, а j –– коэффициенты разложения в этом базисе.)

Как мы видели в главе 2, входом преобразования Фурье является M-мерный комплексный вектор , а результатом преобразования является вектор , для которого

Здесь ! –– корень из единицы степени M (комплексный). По сравнению с главой 2 мы добавили множитель pM. Он нужен для того, чтобы сумма j i j2 равнялась единице, если она равна единице для j i j2.

Непосредственное применение этой формулы требует O(M2) шагов. Но, как мы видели, если M есть степень двойки, есть более эффективный способ,

требующий всего O(M log M) шагов. (Благодаря этому цифровая обработка сигналов становится реальной.) Мы сейчас увидим, что квантовые алгоритмы позволяют экспоненциально ускорить вычисления и выполнить преобразование Фурье за O(log2 M) шагов.

Но, спрашивается, как же время работы алгоритма может быть меньше длины входа? Дело в том, что вход кодируется как коэффициенты суперпозиции m = log M кубитов (у такого состояния как раз 2m = M коэффициентов).

M 1

В наших обозначениях j i = P j jji, где j –– амплитуда m-битового слова,

j=0

являющего двоичной записью числа j. (Можно сказать, что вектора jji обра-

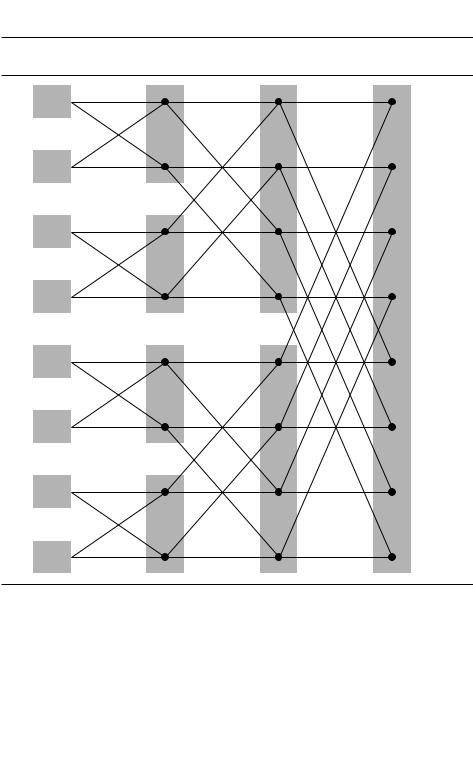
Квантовый алгоритм преобразования Фурье преобразует эту суперпозицию, и это требует m = log M этапов. После выполнения очередного этапа коэффициенты текущей суперпозиции представляют собой промежуточные результаты в схеме быстрого преобразования Фурье. (См. рисунок 10.4, взятый из главы 2.) Как мы увидим, каждый этап может быть реализован как последовательность log M элементарных операций. Таким образом, в общей сложности получается log2 M операций, после которых коэффициенты суперпозиции хранят результат преобразования Фурье.

Таким образом, было бы честнее говорить не о квантовом преобразовании Фурье, а о квантовой выборке из преобразования Фурье:

M 1

Вход: суперпозиция системы из m = log2 M кубитов, j i = P j jji.

j=0

Действия: последовательность из O(m2) = O(log2 M) элементарных квантовых операций с системой, в результате которых она приходит

по распределению вероятностей P(j) = j j j .

Можно сказать, что квантовое преобразование Фурье –– это быстрый способ получить хоть какую-то информацию о результате преобразования Фурье –– а именно, узнать какой-то из его не очень малых коэффициентов. Точнее, мы узнаём не сам коэффициент, а индекс. С первого взгляда трудно себе представить, как можно извлечь пользу из такой скудной информации. Оказывается, что иногда можно –– и мы сейчас обсудим, как.

10.4. Периодичность

Предположим, что последовательность 0, 1, ‌, M 1 имеет период k, где k –– делитель M. Тогда i = j при i j (mod k), и последовательность разбивается на M=k одинаковых участков длины k. Будем говорить, что состояние j i периодично с периодом k и сдвигом j, если в каждом из участков только один член отличен от нуля, и это j , j+k, j+2k, ‌

Рис. 10.5. Примеры периодических состояний (показаны ненулевые коэффициенты).

Для такого состояния выборка из преобразования Фурье (повторённая несколько раз) позволяет с большой вероятностью найти его период. В самом деле, как мы увидим (см. врезку), верно такое утверждение:

Пусть входом квантового алгоритма выборки из преобразования Фурье является состояние с периодом k и сдвигом j, где k –– некоторый делитель M. Тогда индекс на выходе будет кратен M=k, и все кратные M=k одинаково вероятны.

Преобразование Фурье периодического вектора

Рассмотрим вектор j i, который имеет период k и сдвиг 0 (с ненулевыми членами 0, k, 2k, ‌, всего M=k штук). Чтобы сумма квадратов всех мо-

дулей ненулевых членов равнялась 1, сделаем их равными pk=M:

DRAFTнение 10.5 показывает, что сдвиг в аргументе соответствует умножению компонент результата на подходящие множители).

В этом случае преобразование Фурье также будет периодическим с периодом M=k и сдвигом 0:

В правой части стоит геометрическая прогрессия из M=k членов со знаме-

нателем !jk. Если jk кратно M, то знаменатель равен 1, так как ! –– комплексный корень из единицы степени M. Тогда сумма прогрессии равна M=k, так что j = 1=pk при этих j (то есть при j, кратных M=k). Если же jk не кратно M, то можно воспользоваться формулой для суммы геометри-

ческой прогрессии, (1 !jk(M=k))=(1 !jk), в которой теперь знаменатель

то преобразование Фурье по-прежнему будет сосредоточено в кратных

M=k:

Отсюда мы заключаем (по линейности), что у любого состояния с периодом k преобразование Фурье сосредоточено в координатах, кратных M=k. Если к тому же лишь один коэффициент в периоде исходного состояния от-