Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

отвечающие за то, что i-я вершина имеет номер j в гамильтоновом пути. Используя эти переменные, нужно записать ограничения задачи.)

8.6. На странице 249 мы узнали, что задача 3-выполнимости остаётся NP-пол- ной даже для формул, в которых каждый литерал встречается не более двух раз.

(a) Докажите, что если каждый литерал встречается не более одного раза, то задача может быть решена за полиномиальное время.

(b) Докажите, что задача о независимом множестве остаётся NP-полной DRAFTдля графов, в которых степень каждой вершины не выше 4.

8.7. Рассмотрим следующий частный случай задачи выполнимости: каждый дизъюнкт состоит ровно из трёх литералов, каждая переменная встречается не более трёх раз. Докажите, что данная задача может быть решена за полиномиальное время. (Подсказка: в двудольном графе, где слева дизъюнкты, справа переменные, а рёбра соответствуют вхождению переменной в дизъюнкт, есть совершенное паросочетание, см. упражнение 7.30.)

8.8. Входом задачи точной 4-выполнимости (exact 4SAT) является множество дизъюнктов, каждый из которых содержит ровно четыре переменные, причём все эти переменные различны. Найти, как обычно, нужно выполняющий набор. Покажите, что данная задача NP-полна.

8.9. В задаче о множестве представителей (hitting set) на вход даются семейство множеств fS1, S2, ‌, Sng и число b. Требуется найти множество H размера не более b, пересекающее каждое Si (то есть Si \ H 6= ? при всех i), или сообщить, что такого нет. Докажите, что эта задача NP-полна.

8.10. Доказательство NP-полноты обобщением. Покажите, что каждая приведённая ниже задача NP-полна, поскольку она обобщает некоторую уже известную нам NP-полную задачу.

(a) Изоморфизм подграфа (subgraph isomorphism). По двум неориентированным графам G и H выяснить, является ли G подграфом H (то есть можно ли удалить из H некоторые вершины и рёбра так, чтобы остался граф, который с точностью до названий вершин совпадает с G), и если является, указать соответствие между вершинами.

(b) Максимальный путь (longest path). Даны граф G и число g; найти в G простой путь длины не менее g.

(c) Задача максимальной выполнимости (max SAT). По данной формуле в КНФ и числу g найти набор, выполняющий хотя бы g дизъюнктов.

(d) Плотный подграф (dense subgraph). Даны граф G и числа a и b; найти a вершин в G, соединённых друг с другом хотя бы b рёбрами.

(e) Разреженный подграф (sparse subgraph). Даны граф G и числа a и b; найти a вершин в G, между которыми в G есть не более b рёбер.

(f) Покрытие множествами (set cover). Эта задача обобщает две известные нам NP-полные задачи.

(g)Задача о надёжной сети (reliable network). Даны две матрицы размера n n: матрица расстояний di j и матрица требований связности ri j , а также число b. Надо найти граф G = (f1, 2, ‌, ng, E), в котором (1) сумма длин рёбер не превосходит b и (2) между любыми двумя вершинами i и j есть хотя бы ri j путей, не пересекающихся по вершинам. (Подсказка: пусть все di j равны 1 или 2, b = n, а все ri j равны 2. Какая NP-полная задача получается?)

8.11.Есть несколько версий задачи о гамильтоновом пути: граф может быть ориентированным или нет, искать можно путь или цикл. Сведите задачу о гамильтоновом пути в ориентированном графе к следующим двум задачам.

(a)Задача о гамильтоновом пути в неориентированном графе.

(b)Задача о гамильтоновом (s, t)-пути в неориентированном графе (ищется гамильтонов путь с заданным началом s и концом t).

8.12.Задача о k-покрывающем дереве (k-spanning tree) состоит в следующем.

Вход: неориентированный граф G = (V, E).

Выход: покрывающее дерево G, в котором каждая вершина имеет степень не более k.

Покажите, что для любого k ¾ 2

(a)задача о k-покрывающем дереве является задачей поиска (лежит в

NP);

(b)задача о k-покрывающем дереве NP-полна. (Подсказка: начните с k = 2

иустановите связь между этой задачей и задачей о гамильтоновом пути.)

8.13. Для каждой из перечисленных ниже задач предложите полиномиальный алгоритм или докажите NP-полноту. На вход даётся неориентированный граф G = (V, E), а также

(a)множество вершин L V , и надо найти покрывающее дерево, в котором все вершины из L являются листьями;

(b)множество вершин L V , и надо найти покрывающее дерево, в котором листьями являются все вершины из L и только они;

(c) множество вершин L V , и требуется найти покрывающее дерево,

вкотором множество листьев лежит в L;

(d)число k, и надо найти покрывающее дерево, у которого не более k ли-

стьев;

(e)число k, и надо найти покрывающее дерево, у которого не менее k листьев;

(f)число k, и надо найти покрывающее дерево, у которого ровно k листьев.DRAFT

(Подсказка: Все задачи, кроме одной, являются непосредственными обобщениями NP-полных.)

8.14. Докажите NP-полноту следующей задачи: по данному неориентированному графу G = (V, E) и числу k найти клику размера k и независимое множество размера k, если оба искомых объекта есть в графе.

8.15. Докажите, что следующая задача о максимальном общем подграфе NP-полна.

Вход: два графа G1 = (V1, E1), G2 = (V2, E2) и число b.

Выход: два подмножества вершин V10 V1, V20 V2, после удаления которых получатся два одинаковых (изоморфных) графа с не менее чем b вершинами.

8.16. Повар-экспериментатор хочет приготовить новое блюдо, использовав максимальное количество из имеющихся ингредиентов. Некоторые из них плохо сочетаются: для каждых двух ингредиентов i и j (номера от 1 до n) в таблице есть число от 0 до 1 –– штраф за их совместное использование (0 –– нет проблем, 1 –– максимальная несовместимость). Вот пример подобной таблицы с 5 ингредиентами:

DRAFTВ данном примере ингредиенты 2 и 3 сочетаются почти идеально, а 1 и 5 –– крайне плохо. Два естественных свойства таблицы: она симметрична и на диагонали стоят нули. Для любого набора ингредиентов можно вычислить штраф (сумма штрафов по всем парам; например, для f1, 3, 5g получаем 0,2 + 1,0 + 0,5 = 1,7). Мы хотим, чтобы штраф был небольшим. Получаем такую задачу о поваре-экспериментаторе (experimental cuisine):

Вход: число n, матрица штрафов n n и число p ¾ 0.

Выход: вариант с максимально возможным числом ингредиентов и суммарным штрафом не более p.

Покажите, что если эта задача решается за полиномиальное время, то за полиномиальное время можно решить и задачу 3-выполнимости.

8.17. Покажите, что для любой задачи из класса NP существует алгоритм, который решает за время O(2p(n)), где n –– размер входа, а p –– некоторый полином (свой для каждой задачи).

8.18. Докажите, что если P = NP, то криптосистема RSA (раздел 1.4.2) может быть взломана за полиномиальное время.

8.19. Граф с 2n вершинами называется воздушным змеем (kite), если n его вершин образуют клику, а оставшиеся n вершин соединены в путь, начинающийся в одной из вершин клики. В задаче о воздушном змее (kite problem) по данному графу и числу g требуется проверить, есть ли в графе подграф на 2g вершинах, являющийся воздушным змеем. Докажите NP-полноту этой задачи.

8.20. Доминирующим множеством (dominating set) неориентированного графа G = (V, E) называется такое подмножество его вершин D V , что любая вершина графа либо лежит в D сама, либо соединена с вершиной, лежащей в D. Докажите NP-полноту данной задачи.

8.21. Секвенирование путём гибридизации. Пусть мы хотим восстановить последовательность аминокислот в ДНК и узнали (для данного k), какие наборы из k символов она содержит (нашли все подстроки длины k) и сколько раз встречается каждый из них.

DRAFTБолее формально, для строки x обозначим через (x) мультимножество всех её k-подстрок; в нём jxj k + 1 элементов (каждый с учётом кратности). Нам нужно по данному мультимножеству строк длины k найти строку x, для которой (x) именно такое.

(a) Сведите эту задачу к задаче о гамильтоновом пути. (Подсказка: постройте ориентированный граф, вершинами которого будут все данные подстроки, а рёбра соединяют a и b, если последние k 1 символов a совпадают с первыми k 1 символами b.)

(b) Мало того, эта задача также сводится к задаче об эйлеровом пути. (Подсказка: на этот раз данные подстроки задают рёбра графа.)

8.22. Представим последовательно выполняемые дела в виде ориентированного графа (ребро из i в j означает, что i должно предшествовать j). Иногда ограничения противоречат друг другу (если в графе есть цикл). Мы хотим удалить минимальное количество рёбер так, чтобы после этого циклов не осталось.

Подмножество рёбер E0 E ориентированного графа G = (V, E) называется множеством обратной связи (feedback arc set), если удаление этих рёбер делает граф ациклическим.

Задача: по данному ориентированному графу G = (V, E) и числу b найти множество обратной связи размера не более b.

(a) Докажите, что данная задача NP-полна.

Это можно сделать, сведя к ней задачу о вершинном покрытии. Пусть дан неориентированный граф G = (V, E) и мы хотим найти в нём вершинное покрытие размера не более b. Пусть V = fv1, ‌, vng. Построим ориентированный граф G0 = (V 0, E0), в котором V 0 состоит из 2n вершин w1, w10 , ‌, wn, wn0 , а E0 содержит n + 2jEj (ориентированных) рёбер:

ff (wi , wi0) для всех i = 1, 2, ‌, n;

ff (wi0, wj ) и (w0j , wi ) для всех (vi , vj ) 2 E.

(b) Покажите, что если в G есть вершинное покрытие размера b, то в G0 есть множество обратной связи размера b.

(c) Покажите обратное: если в G0 есть множество обратной связи размера b, то в G есть вершинное покрытие размера b. (Подсказка: удобно сперва слегка переделать данное множество обратной связи размера b, не увеличивая его размер, после чего построить по нему вершинное покрытие того же размера, что и переделанное множество.)

8.23. В задаче о путях без общих вершин (node disjoint paths) на вход даётся неориентированный граф, в котором некоторые вершины s1, ‌, sk помечены как «истоки», а некоторые вершины t1, ‌, tk –– как «стоки». Требуется соединить все si с соответствующими ti путями, не имеющими общих вершин. Мы хотим доказать NP-полноту этой задачи; следующие пункты указывают способ это сделать (чем дальше –– тем подробнее).

(a) Сведите к ней задачу 3-выполнимости.

(b) Для формулы в 3-КНФ с n переменными и m дизъюнктами используйте DRAFTk = m + n пар исток-сток. Заведите пару исток-сток (sx , tx ) для каждой переменной x и пару исток-сток (sc , tc ) для каждого дизъюнкта c.

(c) Для каждого дизъюнкта введите 6 промежуточных вершин, соответствующих литералам дизъюнкта и их отрицаниям.

(d) Если путь из sc в tc проходит через промежуточную вершину, соответствующую некоторому литералу, то никакой другой путь уже не может проходить через эту вершину. Как использовать это, чтобы обеспечить согласованность выбора истинных литералов в разных дизъюнктах?

Глава 9

Решение NP-полных задач

DRAFTПосмотрим на ситуацию с точки зрения практики. Возникла какая-то задача про графы, и нужно написать программу, её решающую. Чем может помочь наша теория? Если повезёт, задача может оказаться вариантом какой-то из разобранных или сводиться к ним, или решаться каким-то известным приёмом (динамическое или линейное программирование, минимальные покрывающие деревья, потоки) –– хотя не всегда легко это сразу заметить. Такое везение, увы, бывает редко –– наугад взятая задача поиска скорее окажется NP-полной, и что тогда?

Для начала можно доказать, что ваша задача NP-полна. Возможно, ка- кая-то из стандартных задач является её частным случаем (см. обсуждение на с. 253 и упражнение 8.10), или можно свести к ней одну из NP-полных задач (скажем, выполнимость или УНЕ). Но что это даёт? Конечно, поупражняться всегда полезно, к тому же приятно осознавать, что дело не в недостатке умения, а в сложности задачи. Но можно ли сделать что-то ещё?

Иногда можно, несмотря на доказанную NP-полноту задачи –– не исключено, что на практике попадаются несложные случаи. Скажем, NP-полнота задачи выполнимости не страшна, если нас интересуют (как в логическом программировании) только хорновские формулы (см. раздел 5.3). Другой пример: если реально интересующие нас графы представляют собой деревья, то трудные для произвольных графов задачи (например, задача о независимом множестве) могут быть решены быстро при помощи динамического программирования (раздел 6.7).

К сожалению, такой подход работает не всегда –– задача может остаться NP-полной и после ограничения. Скажем, задача выполнимости остаётся полной для дизъюнктов с тремя литералами, а задача о независимом множестве (и многие другие) –– для планарных графов (графов, которые можно нарисовать на плоскости без пересечений). Да и понять, какие частные случаи нужны на практике, не просто. Что ж, тогда можно попытаться хотя бы оптимизировать перебор (см. раздел 9.1 о переборе с возвратом и методе ветвей и границ) –– вдруг этого хватит для практически важных случаев.

С другой стороны, можно смириться с тем, что оптимального решения мы не найдём, и удовлетвориться решением, которое не сильно хуже оптимального. Например, в разделе 5.4 мы рассмотрели жадный алгоритм, который гарантирует, что найденное семейство покрывающих множеств отличается от оптимального не более чем в log n раз. Алгоритмы, дающие подобные гарантии, называют приближёнными (approximation algorithms), и они известны для многих NP-полных оптимизационных задач (см. раздел 9.2). Часто они

268 Глава 9. Решение NP-полных задач

очень изящны (хотя и не просты). С другой стороны, и тут есть некоторый барьер: для некоторых NP-полных задач доказано, что отыскание приближённых решений с точностью лучше некоторой границы означало бы P = NP.

На худой конец бывают и «эвристические» алгоритмы, которые в принципе ничего не гарантируют (ни времени работы, ни качества приближения), но могут реально работать, если их автор достаточно изобретателен, имеет опыт работы в данной области, долго подбирал параметры и придумывал разные улучшения, или воспользовался идеей из физики или биологии. Некоторые примеры такого рода рассмотрены в разделе 9.3.

9.1. Оптимизация перебора

9.1.1. Перебор с возвратом

Иногда можно понять, что выбранный путь –– тупиковый. Например, если мы

(w x y z), (w ¯x), (x ¯y), (y ¯z), (z ¯w¯), (¯w¯ ¯z).

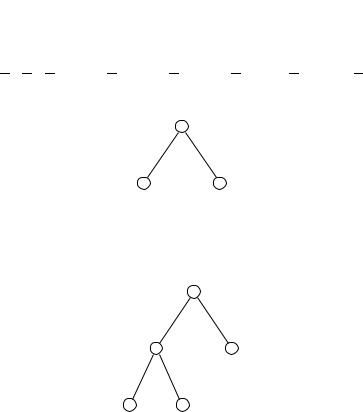
Будем подбирать значения переменных по очереди, начав с w: исходная формула '

w = 0 w = 1

Оба варианта w = 0 и w = 1 допустимы (ни один из дизъюнктов не становится заведомо ложным), так что надо оставить обе ветви поиска. Начать можно с любой, выбрав в ней следующую переменную, например, так:

ложным, и эту ветвь поиска можно закрыть, признав тупиком. Поиск продолжается в одной из двух оставшихся активных вершин.

Таким образом, перебор с возвратом исследует возможные наборы, наращивая дерево только в тех вершинах, где выполняющий набор всё ещё возможен, и останавливается, когда такой набор найден.

Для задачи выполнимости булевой формулы в каждой вершине дерева поиска есть частичный набор значений переменных и множество дизъюнктов, остающихся при подстановке этих значений в исходную формулу. Например, если w = 0 и x = 0, то все дизъюнкты, содержащие ¯w¯ или ¯x, а также вхождения w и x в другие дизъюнкты могут быть удалены, так как первые всегда

где пустой дизъюнкт ( ) свидетельствует о том, что формула уже не может быть выполнена. Таким образом, подзадача для каждой вершины сама имеет вид задачи выполнимости.

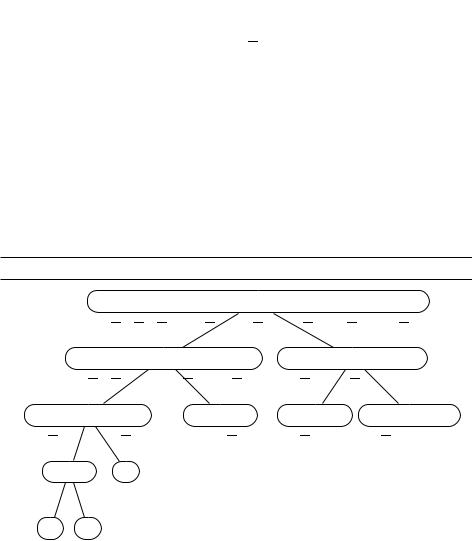
На каждом шаге поиска нужно решать, какую ветвь выбрать и по какой переменной расщеплять на два случая. Хочется сократить пространство поиска, это происходит при появлении пустых дизъюнктов. Поэтому логично выбирать подзадачу с наиболее коротким условием-дизъюнктом и расщеплять по одной из его переменных. Если в этом дизъюнкте окажется всего один литерал, то одну из ветвей можно будет сразу отбросить. (Если это не определяет выбор однозначно, то из разных подзадач логично выбирать ту, которая ниже по дереву, поскольку она, возможно, ближе к выполняющему набору.) На рисунке 9.1 изображено итоговое дерево для рассмотренного выше примера.

Рис. 9.1. Перебор с возвратом показывает, что формула ' невыполнима.

В общем случае, алгоритм перебора с возвратом содержит тест, который по данной подзадаче быстро выдаёт один из трёх ответов:

1)неудача: подзадача не имеет решения;

2)успех: найдено решение подзадачи;

3)неопределённость.

В нашем примере тест даёт ответ «неудача», если текущая формула содержит пустой дизъюнкт; «успех», если формула пуста (не содержит ни одного

дизъюнкта); «неизвестно» –– в остальных случаях. DRAFTОбщий вид алгоритма перебора с возвратами:

начать с некоторой задачи P0

S fP0g {множество активных подзадач} пока S не пусто:

выбрать подзадачу P 2 S и удалить её из S разбить P на меньшие подзадачи P1, P2, ‌, Pk для каждой Pi :

если тест(Pi ) = успех: вернуть найденное решение если тест(Pi ) = неудача: отбросить Pi

иначе: добавить Pi в S сообщить, что решения нет

Процедура выбрать выбирает одну из подзадач, а разбить выбирает переменную для расщепления и строит две подзадачи для двух вариантов её значения. (Мы уже обсуждали способы такого выбора.)

При удачном подборе и реализации процедур тест, выбрать и разбить перебор с возвратами может быть вполне практичным: рассмотренный нами алгоритм поиска для задачи выполнимости лежит в основе многих успешно работающих на практике программ. Дополнительным подтверждением его эффективности является то, что выполнимость формул в 2-КНФ он проверяет за полиномиальное время (упражнение 9.1).

9.1.2. Метод ветвей и границ

Рассмотренный метод может быть использован не только для задач поиска (в нашем примере –– задачи выполнимости), но и для задач оптимизации. Допустим, мы решаем задачу минимизации (для задачи максимизации всё аналогично).

Как и раньше, мы рассматриваем частичные решения. Нам необходимо понять, какие из них заведомо не приведут к оптимальному решению, чтобы их отбросить и сэкономить время. Отбросить подзадачу можно, если мы знаем, что на этом пути получится решение, худшее уже найденного в другой ветви. Но откуда мы это можем узнать? Для этого надо использовать нижнюю оценку стоимости решения.

начать с некоторой задачи P0

SfP0g {множество активных подзадач}

текущий_минимум 1