Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

7.6.2. Алгоритм

На каждой итерации симплекс-метод должен:

1)проверить, является ли текущая вершина оптимальной (и если это так, то остановиться);

2)решить, куда переходить дальше.

Как мы увидим, обе задачи просты, если текущая вершина находится в начале координат. А если вершина находится где-то ещё, то мы просто преобразуем систему координат, сделав текущую вершину началом.

Для начала посмотрим, почему начало координат удобно. Пусть мы имеем некоторую линейную программу общего вида

cT x ! max

Ax ¶ b x ¾ 0

где x = (x1, ‌, xn) –– вектор из переменных. Пусть начало координат является допустимым. Тогда оно, очевидно, является вершиной, так как это единственная точка, в которой n неравенств fx1 ¾ 0, ‌, xn ¾ 0g обращаются в равенство. (Мы предполагаем вершину невырожденной, так что другие неравенства в равенства не обращаются.) Шаг симплекс-метода, как мы говорили, состоит из двух частей. Для первой:

Начало координат оптимально тогда и только тогда, когда ci ¶ 0 для всех i.

Действительно, если ci ¶ 0 для всех i, то при x ¾ 0 рассчитывать на лучшее (положительное) значение целевой функции мы не можем. Обратно, если ci > 0 для какого-то i, то начало координат не оптимально, так как мы можем увеличить значение целевой функции, увеличив xi . (Напомним, что по предположению остальные неравенства не обращаются в равенства, так что xi можно хотя бы немного увеличить.)

Если начало координат не оптимально, можно переместиться по некоторому ребру, увеличив некоторое xi , для которого ci > 0. Насколько мы можем увеличить xi ? Пока мы не столкнёмся с каким-то другим ограничением. Другими словами, мы делаем одно из определяющих вершину неравенств xi ¾ 0 строгим и увеличиваем xi до тех пор, пока какое-то другое неравенство, до этого выполнявшееся с запасом, не обратится в равенство. При этом мы снова имеем n равенств, то есть мы находимся в новой вершине.

Например, пусть мы имеем дело со следующей линейной программой:

2x1 + 5x2 ! max

212 Глава 7. Линейное программирование

Симплекс-метод можно запустить в начале координат, которое задаётся ограничениями ○4 и ○5 . Для перехода мы «освобождаем» ограничение x2 ¾0, превращая его из равенства в строгое неравенство. Увеличивая x2, мы прежде всего наталкиваемся на ограничение x1 + x2 ¶3, и поэтому должны остановиться на x2 = 3, в точке, где это новое неравенство обращается в равенство. Новую вершину задают неравенства ○3 и ○4 .

Таким образом, мы знаем, что делать, если мы находимся в начале координат. Но что если наша текущая вершина u расположена где-то ещё? Мы

сводим этот случай к уже рассмотренному с помощью линейного преобразо- DRAFTвания координат. В качестве новых координат мы выбираем те самые линей-

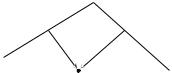
ные функции, которые использованы в определяющих точку неравенствах, сдвинутые в нуль. Другими словами, новые координаты точки x пропорциональны расстояниям y1, ‌, yn от точки x до гиперплоскостей, пересечением которых является вершина u:

u

y2 y1

x

Более точно, если одно из неравенств, задающих вершину, имеет вид ai x ¶ bi , то расстояние от точки x до грани, соответствующей этому неравенству, пропорционально

yi = bi ai x.

Получаем n линейных функций yi , по одной на каждую грань, причём переход от x к y можно обратить и выразить xi как линейную функцию от yj . Таким образом, мы можем переписать всю линейную программу в переменных yi . Получаем эквивалентную линейную программу (например, оптимальное значение остаётся тем же), но записанную в другой системе координат.

1. Новая программа содержит неравенства y ¾0, в которые преобразуются неравенства, задающие u.

2. Точка u становится началом координат y-пространства.

3. Целевой функцией становится cu + c˜T y, где cu –– это значение целевой функции в u, а c˜ –– преобразованный вектор коэффициентов целевой функции в новых координатах.

В результате мы вернулись к случаю, с которым уже умеем работать! На рисунке 7.13 описанный алгоритм применяется к нашему примеру.

Теперь симплекс-метод полностью описан. Он переходит от вершины к соседней вершине, останавливаясь, когда дальнейшее увеличение целевой функции невозможно, то есть когда все коэффициенты её выражения в новых координатах меньше или равны 0. Как мы уже говорили, вершина с этим свойством даёт глобальный оптимум. Пока текущая вершина не является локально оптимальной, её локальная система координат включает некоторое

Рис. 7.13. Пример работы симплекс-метода.

направление, по которому целевую функцию можно улучшить, так что мы сдвигаемся в этом направлении (по соответствующему ребру многогранника), пока не попадём в соседнюю вершину. В силу предположения о невырожденности (см. сноску на с. 210), это ребро имеет ненулевую длину, и поэтому мы улучшаем значение целевой функции. Таким образом, процесс рано или поздно должен остановиться (вершин конечное число).

214 Глава 7. Линейное программирование

7.6.3. Тонкости

В симплекс-методе есть ряд важных моментов, которые мы ещё не рассмотрели.

Начальная вершина. Как нам найти вершину, из которой запускать алгоритм? В наших двумерных и трёхмерных примерах мы всегда начинали из начала координат: эта точка не только лежала в области допустимых значений, но и была её вершиной. Для произвольной линейной программы это не гарантировано: вообще говоря, мы заранее не знаем ни одной допустимой DRAFTточки. Но оказывается, поиск такой точки можно свести к некоторой линейной программе, которую можно решить с помощью того же симплекс-метода!

Чтобы увидеть, как это делается, начнём с произвольной линейной программы в стандартном виде (см. раздел 7.1.4):

cT x ! min, где Ax = b и x ¾ 0.

(Мы хотим найти какое-либо решение; на этом этапе вектор c роли не играет.) Можно считать, что все правые части уравнений неотрицательны: если bi < 0, то мы просто умножаем обе части i-го уравнения на 1.

Далее мы следующим образом записываем новую линейную программу:

ff Вводим m вспомогательных переменных z1, ‌, zm ¾ 0, где m –– количество уравнений.

ff Модифицируем уравнения, добавляя zi к левой части i-го уравнения. ff Целевой функцией для минимизации будет z1 + z2 + ‌ + zm.

Для этой новой линейной программы легко получить допустимую точку –– пусть zi = bi для всех i, а все другие переменные равны нулю. Затем можно воспользоваться симплекс-методом, чтобы получить оптимальное решение.

Имеются две возможности. Если в этом решении значение z1 + ‌ + zm нулевое, то все zi –– нули, а значит, оптимальная вершина для новой линейной программы является допустимой вершиной исходной линейной программы. Мы можем забыть про zi и (наконец-то) запустить симплекс-метод для исходной задачи!1

Но оптимальное значение целевой функции может оказаться ненулевым. Что это означает? Мы пытались минимизировать сумму zi , но симплекс-ме- тод установил, что она не может быть нулевой. Значит, исходная линейная программа несовместна: ей требуются какие-то ненулевые zi , чтобы свести концы с концами. Тем самым мы, использовав симплекс-метод, обнаружили несовместность линейной программы.

Вырождение. У многогранника на рисунке 7.12 вершина B вырожденная, то есть принадлежит более чем трём граням многогранника (в данном случае

1Тут есть ещё одна тонкость: имея допустимую точку, надо найти вершину. Изменяя значение какой-то из переменных до тех пор, пока одно из неравенств не превратится в равенство, можно попасть на границу области. Затем можно двигаться по грани, сохраняя полученное равенство, пока ещё одно неравенство не обратится в равенство, и так далее. Мы не будем обсуждать это подробно.

○2 , ○3 , ○4 , ○5 ). Алгебраически это означает, что из четырёх плоскостей, проходящих через эту вершину, можно оставить любые три ({○2 ,○3 ,○4 }, {○2 ,○3 ,○5 }, {○2 ,○4 ,○5 } или {○3 ,○4 ,○5 }), и соответствующая система с тремя уравнениями от трёх неизвестных имеет единственное решение –– нашу вершину

(0, 300, 100).

Для симплекс-метода это создаёт проблемы: естественно задавать вершину набором неравенств, которые в ней обращаются в равенства, а соседство понимать как замену одного из равенств на другое. Но в вырожденном случае такое задание уже не однозначно и соседство уже так просто не описыва- DRAFTется. Другая возможность вырождения –– когда движение по ребру не меняет значения целевой функции (что создаёт потенциальную возможность зацикливания).

Один из способов избавиться от этих проблем –– произвести шевеление (perturbation): добавить к коэффициентам небольшие случайно выбранные числа. С практической точки зрения это не играет роли, так как изменения очень малы. Зато теперь можно быть уверенным, что вырожденных вершин не будет –– вероятность того, что после случайного шевеления сдвинутые плоскости ○2 , ○3 , ○4 , ○5 по-прежнему пересекутся в одной точке, равна нулю.

Неограниченность. В некоторых случаях линейная программа не ограничена в том смысле, что целевая функция может быть сделана произвольно большой (или малой, если речь о задаче минимизации). В таком случае сим- плекс-метод это обнаружит следующим образом. На каждой итерации алгоритм пытается увеличить текущее значение целевой функции, увеличивая некоторое xi , для которого соответствующий коэффициент ci целевой функции строго положителен. При этом то, насколько можно увеличить xi , определяется оставшимися ограничениями. Если же эти ограничения не мешают увеличивать xi до бесконечности, то целевая функция не ограничена. В этом случае симплекс-метод останавливается и сообщает об ошибке.

7.6.4. Время работы симплекс-метода

Каково время работы симплекс-метода для линейной программы общего вида

cT x ! max, где Ax ¶ 0 и x ¾ 0,

если в ней n переменных и A содержит m ограничений-неравенств? Так как это итеративный алгоритм, который переходит от вершины к вершине, давайте начнём с оценки времени работы одной итерации. Пусть u –– текущая вершина. По определению, это единственная точка, в которой n ограниче- ний-неравенств обращаются в равенства. Каждая из соседних с ней вершин также использует n 1 из этих неравенств, так что u может иметь не более nm соседей: нужно выбрать, какое неравенство отбросить, а какое новое добавить.

Можно было бы для каждого потенциального соседа проверить, действительно ли он является некоторой вершиной многогранника, и вычислить значение целевой функции. Второе несложно (скалярное произведение требует

n умножений), но проверка того, что перед нами действительно вершина, требует решения системы из n уравнений с n неизвестными (состоящей из неравенств, обращающихся в равенства) и проверки допустимости результата. При использовании метода Гаусса (см. следующую врезку) это занимает время O(n3), что даёт большое время работы: O(mn4) на одну итерацию.

Метод Гаусса

x2 + 3x3 + x4 = 5

Если прибавить к одному уравнению другое (возможно, с каким-то коэффициентом), получим эквивалентную систему. Прибавим первое уравне-

x2 + 2x3 x4 = 2 x2 + 3x3 + x4 = 5

Коэффициент подобран так, чтобы исключить переменную x1 из третьего уравнения (оставив только одно уравнение с x1). Получилась система с тремя уравнениями и тремя неизвестными x2, x3, x4: решив её, мы подставим решение в первое уравнение и найдём x1.

функция Gauss(E, X )

{Вход: система E из n уравнений с n неизвестными X = fx1, ‌, xng,

i-е уравнение ei : ai1 x1 + ai2 x2 + ‌ + ain xn = bi .}

{Выход: решение системы, если оно существует и единственно.}

если все коэффициенты ai1 равны нулю:

вернуть «система несовместна или линейно зависима» если n = 1: вернуть b1=a11

выбрать коэффициент ap1 с наибольшим абсолютным значением поменять местами уравнения e1 и ep

(Мы заботимся о том, чтобы коэффициент, на который нужно делить, был побольше –– деление на малые числа приводит к большой погрешности.)

Метод Гаусса выполняет O(n2) арифметических операций, уменьшая n на 1; всего будет O(n3) операций. Но операции эти проводятся с рациональными числами, числители и знаменатели которых могут расти по ходу дела, так что для честной оценки времени работы надо бы ещё оценить битовый размер возникающих чисел. Это можно сделать, но в такие по-

дробности мы входить не будем.

DRAFTметод действительно производит экспоненциальное число итераций. Другими словами, симплекс-метод является экспоненциальным по времени. Однако подобные экспоненциальные примеры практически не встречаются, и это делает симплекс-метод полезным на практике алгоритмом.

К счастью, можно уменьшить множитель mn4 до mn, тем самым сделав симплекс-метод применимым на практике. Вспомним, что мы для каждой вершины переписывали систему в локальных координатах (раздел 7.6.2) и что на каждом шаге меняется только одна из этих координат. В результате на каждой итерации расходы по переписыванию линейной программы в новых

локальных координатах составляют всего лишь O((m + n)n).

Выбирая соседа с лучшим значением целевой функции, вспомним, что це-

левая функция имеет (в локальных координатах) вид cu + c˜ y, где cu –– значение целевой функции в u. Это сразу определяет перспективное направление перехода: мы выбираем произвольное ˜ci > 0 (если такого нет, то текущая вершина оптимальная, и симплекс-метод останавливается). Определить, на сколько можно увеличить yi , тоже легко, так как неравенства уже переписаны в локальных координатах, и остаётся разрешить их относительно yi . Так мы либо находим следующую точку, либо (если можем увеличивать yi бесконечно) узнаём, что линейная программа не ограничена.

Итак, время работы одной итерации симплекс-метода –– всего O(mn). Но сколько всего может быть итераций? Ясно, что их не может быть больше,

чем вершин, которых не больше Cmn +n. Но эта верхняя оценка экспоненциальна по n. Существуют примеры линейных программ, для которых симплекс-

7.7. Эпилог: вычисление значения схемы

Мы уже видели, что многие задачи сводятся к задаче линейного программирования. Сейчас мы подтвердим это, показав, что в некотором смысле все задачи, разрешимые за полиномиальное время, сводятся к задаче линейного программирования.

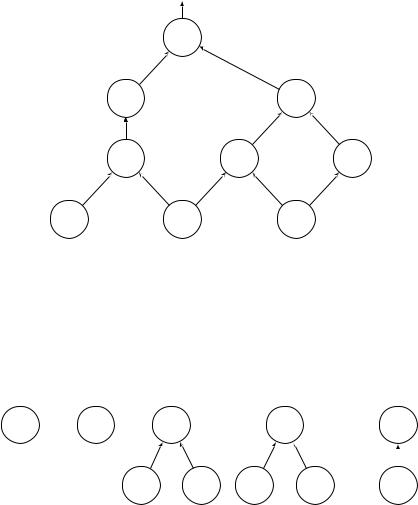
Рассмотрим для начала одну из таких (разрешимых за полиномиальное время) задач. Пусть нам дана булева схема, то есть ациклический ориентированный граф, состоящий из функциональных элементов следующих типов.

ff Входные элементы имеют нулевую входящую степень и значение true или false.

DRAFT1Это утверждение выглядит бессодержательным, поскольку эта задача сама разрешима за полиномиальное время, так что и линейное программирование не нужно. На самом деле в этом разделе речь идёт о более ограниченном виде сводимости, когда память сводящего алгоритма логарифмически ограничена. Мы не будем обсуждать это подробно, ограничившись описанием конкретного свед´ения.

Пример булевой схемы приведён на рисунке. Задача состоит в вычислении значения схемы: что будет на выходе при данных значениях на входах? (При вычислении надо обходить элементы в порядке топологической сортировки и выполнять указанные булевы операции для уже известных входов.)

Линейное программирование за полиномиальное время

Симплекс-метод не является полиномиальным (время работы не ограничено полиномом от размера входа). Для некоторых линейных программ он обходит экспоненциально много вершин, хотя на практике такое случается редко. Долгое время линейное программирование считалось парадоксальной задачей, которая решается быстро на практике, но не в теории.

Однако в 1979 году молодой советский математик Леонид Хачиян доказал, что некоторый другой алгоритм решения задач линейного програм- DRAFTмирования, называемый методом эллипсоидов, решает любую задачу линейного программирования за полиномиальное время. Вместо того чтобы искать решение, переходя от одного угла многогранника к другому, алгоритм Хачияна заключает решение во всё меньшие эллипсоиды (сплющенные многомерные шары). Сам по себе метод довольно прост, но доказательство его корректности сложное. Публикация этого алгоритма, как и (много раньше) запуск первого спутника, стала эффектным достижением, в разгар холодной войны обеспокоившим американские власти возможным отставанием от СССР. На практике метод эллипсоидов так и не заменил симплекс-метод, несмотря на своё теоретическое значение. Вышло ещё более парадоксально: для задачи линейного программирования есть два эффективных алгоритма, но один эффективен только теоретически, а

другой –– только практически.

Несколько лет спустя Нарендра Кармаркар (Narendra Karmarkar), аспирант университета Беркли, придумал совершенно другую идею, которая привела к ещё одному (доказуемо) полиномиальному алгоритму для задачи линейного программирования. Алгоритм Кармаркара известен как метод внутренней точки, потому что он движется к оптимуму не от одной вершины к другой (по рёбрам), как это делает симплекс-метод, а разумно «срезая» путь внутри многогранника. И он таки практически полезен.

Но, возможно, наибольшим достижением оказались не теоретический прорыв Хачияна и не новый подход Кармаркара сами по себе, а возникшее соревнование между симплекс-методом и методом внутренней точки, в результате которого появились очень быстрые алгоритмы для задач линейного программирования.

Эти ограничения вынуждают все элементы принимать правильные значения –– 0 для false и 1 для true. Нам не нужно ничего максимизировать или минимизировать, и мы можем прочитать ответ в переменной xout, соответствующей выходному элементу.

В чём интерес задачи о вычислении значения схемы? Она в некотором смысле является наиболее общей задачей среди всех решаемых за полиномиальное время! Это можно объяснить примерно так: в конечном счёте всякий алгоритм исполняется компьютером, а компьютер по существу представляет собой булеву схему. Правда, один и тот же бит в памяти компьютера последовательно принимает разные значения. С учётом этого работу компьютера