Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

Теперь нам предстоит создать тройки, которые будут моделировать дизъ-

юнкты. Для дизъюнкта c = (x _ ¯y _ z) заведём мальчика bc и девочку gc . Каждый из них будет входить в три тройки, соответствующие трём литералам нашего дизъюнкта. Эти три тройки должны отражать три способа выполнить дизъюнкт: (1) x = true, (2) y = false, (3) z = true. Для (1) возьмём тройку (bc , gc , px1), где px1 –– это p1 в конструкции для x. Эту тройку можно использовать, если p1 остался свободным, то есть если x = true. Аналогичным образом добавим тройки для литералов ¯y и z (одну из троек (bc , gc , py0) или (bc , gc , py2), а также одну из троек (bc , gc , pz1) или (bc , gc , pz3)). Возможность подобрать домашнее животное для bc и gc означает, что дизъюнкт c выполнен.

DRAFTщую bc , gc и животное, оставшееся свободным при выбранном значении переменной).

Тут есть проблема: если один и тот же литерал встречается в нескольких дизъюнктах, то может не хватить животных: для каждой переменной их только два (для каждого из двух её возможных значений). Но мы уже знаем, как переделать формулу в такую, где каждый литерал встречается не более двух раз, и тогда их хватит, потому что в каждом блоке есть два животных для пе-

ременной и два для её отрицания.

Кажется, что всё готово. По решению полученной задачи о трёхдольном сочетании легко восстановить выполняющий набор для исходной формулы: для каждой переменной надо посмотреть на изображающий её блок. Напротив, чтобы по выполняющему набору построить трёхдольное сочетание, закодируем значения переменных на языке блоков, то есть возьмём трой-

Осталась одна небольшая тонкость: в построенном трёхдольном сочетании могли остаться беспризорные животные, и даже понятно сколько: если в формуле n переменных и m дизъюнктов, то 2n m питомцев не попадут в тройки (тут всё сходится: это число неотрицательно, поскольку каждая переменная входит в формулу не более трёх раз, а каждый дизъюнкт содержит не менее двух литералов). Понятно, как тут быть: добавим 2n m пар маль- чик-девочка, которым годятся любые животные (то есть добавим все тройки, включающие одну из таких пар и одно животное).

Трёхдольное сочетание ! уравнения в нулях и единицах

Напомним, что входом задачи УНЕ является битовая матрица A размера m n, а найти нужно битовый вектор x = (x1, ‌, xn), удовлетворяющий уравнению

Ax = 1,

где через 1 обозначен вектор из единиц. Как же сформулировать задачу о трёхдольном сочетании в этих терминах?

Это несложно: искомый объект (в данном случае трёхдольное сочетание) описывается переменными, а уравнения задают ограничения. Как это сде-

лать в нашем случае? Пусть у нас m мальчиков, m девочек, m животных, а также n троек. Заведём n булевых переменных x1, ‌, xn, по одной для каждой тройки; xi = 1 означает, что i-я тройка вошла в сочетание.

Теперь нужно записать уравнения, гарантирующие, что решение, задаваемое переменными x1, ‌, xn, является корректным сочетанием. Рассмотрим какого-нибудь мальчика. Пусть он входит в тройки с номерами j1, ‌, jk. Нам надо записать, что выбрана ровно одна из этих троек:

Столбцы матрицы A соответствуют пяти представленным тройкам, а строки соответствуют Андрею, Борису, Владимиру, Вере, Надежде, Любови, кошке, собаке и канарейке.

Убедиться в том, что решения для этих задач переделываются одно в другое, не представляет никакого труда.

УНЕ ! сумма подмножества

Данное сведение связывает два частных случая задачи целочисленного линейного программирования: в обоих случаях переменные булевы, но в одном случае много уравнений с коэффициентами 0 и 1, а в другом –– всего одно уравнение, но зато с произвольными целочисленными коэффициентами. Идея сведения простая, но важная: целые числа можно задавать с помощью битовых векторов.

Для примера рассмотрим такую матрицу:

Мы ищем столбцы матрицы A, которые при сложении дают вектор из одних единиц. Столбцы матрицы можно интерпретировать как числа в двоич-

ной системе счисления (младшие разряды снизу), тогда задача преобразуется в такую: нужно выбрать некоторые из чисел 18, 5, 4, 8, получив сумму 111112 = 31. Таким образом, мы построили сведение задачи УНЕ к задаче о сумме подмножества.

За исключением одной детали –– мы забыли про переносы. Из-за переносов сумма пятибитовых чисел может оказаться равной 31, даже когда сумма соответствующих векторов не равна (1, 1, 1, 1, 1): например, 5 + 6 + 20 = = 001012 + 001102 + 101002 = 111112 = 31. Но побороть эту проблему в нашем случае просто: будем рассматривать столбцы матрицы как записи чисел DRAFTне в двоичной системе счисления, а в системе по основанию (n + 1). Тогда переносов просто не будет (поскольку слагаемых не больше n, а все цифры –– нули или единицы).

УНЕ ! ЦЛП

Если одна задача является частным случаем другой, то сведение (частной задачи к общей) тривиально: обе функции f и h (см. диаграмму сведения на с. 242) тождественны. Скажем, задача 3-выполнимости является частным случаем задачи выполнимости. Это простое замечание часто оказывается полезным: скажем, задача о покрытии множествами NP-полна, потому что она обобщает задачу о вершинном покрытии (а заодно и задачу о трёхдольном сочетании). В упражнении 8.10 приведено ещё несколько подобных примеров.

То же самое (с точностью до небольшой переформулировки) относится к сведению УНЕ к ЦЛП. В задаче ЦЛП мы хотим найти целочисленный вектор x, для которого Ax ¶b. Чтобы записать в такой форме вход задачи УНЕ (систему уравнений с булевыми переменными), нужно всего лишь переписать каждое равенство как два неравенства (как мы делали в разделе 7.1.4) и ещё для каждой переменной xi добавить два неравенства xi ¶ 1 и xi ¶ 0.

УНЕ ! гамильтонов цикл

В задаче о гамильтоновом цикле мы ищем в графе цикл, который проходит через каждую вершину ровно один раз. Мы докажем NP-полноту этой задачи в два приёма: сначала мы сведём УНЕ к чуть более общей задаче о гамильтоновом цикле с парными рёбрами, после чего поймём, как свести это обобщение к исходной задаче о гамильтоновом цикле.

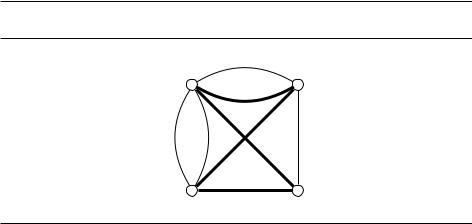
В задаче о гамильтоновом цикле с парными рёбрами дан граф G = (V, E) и множество C E E пар рёбер. Необходимо найти цикл, который: (1) как и в исходной задаче, проходит через каждую вершину ровно один раз и (2) для каждой пары рёбер (e, e0) 2 C проходит ровно по одному из этих рёбер. На рис. 8.10 показан пример такой задачи; решение выделено жирными линиями. Заметьте, что теперь мы разрешаем кратные рёбра (несколько рёбер, соединяющих одни и те же вершины). Во многих задачах на графах смысла в таких дублирующих рёбрах нет, но в рассматриваемой нами сейчас задаче это осмысленно, потому что в разные пары могут входить разные копии одного и того же ребра.

Рис. 8.10. Задача о гамильтоновом цикле в графе с парными рёбрами (множество C равно f(e1, e3), (e5, e6), (e4, e5), (e3, e7), (e3, e8)g) и её решение.

Итак, начнём сводить УНЕ к гамильтонову циклу с парными рёбрами. Имея систему уравнений Ax = 1 (где A –– это матрица размера m n из нулей и единиц, задающая m уравнений от n переменных) мы построим (см. рис. 8.11) цикл, соединяющий m + n семейств кратных рёбер. Для каждой переменной xi в нём два кратных ребра (соответствующих случаям xi = 0 и xi = 1). Для каждого уравнения x j + ‌ + x j = 1 с k переменными будет коллекция из k кратных рёбер, по одному1 дляk каждой переменной. Ясно, что гамильтонов цикл в таком графе должен «выбрать» значение для каждой переменной и «выбрать» по одной переменной в каждом уравнения.

Конечно, это ещё не всё. Мы пока отразили в графе только размеры матрицы A, но не её структуру –– легко догадаться, что для этого мы используем возможность указывать пары рёбер. Для каждого уравнения (напомним, что их m штук) и каждой переменной xi из этого уравнения добавим в C пару (e, e0), где e –– ребро, соответствующее вхождению этой переменной в это уравнение (слева на рисунке 8.11), а e0 –– ребро, соответствующее случаю xi = 0 (на рисунке справа). Этим мы вынуждаем ту переменную в уравнении, через которую прошёл цикл, быть истинной, а остальные быть ложными. На этом конструкция завершена.

Почему это работает? Рассмотрим любое решение полученной задачи о гамильтоновом цикле с парными рёбрами. Как мы уже говорили, такое решение выбирает значение для каждой переменной, а также выбирает по одной переменной в каждом уравнения. Проверим, что выбранные таким образом значения удовлетворяют всем уравнениям. Условия на пары гарантируют, что те переменные, через которые цикл не проходит в левой половине, равны 0, а те, через которые цикл проходит, равны 1. Поэтому в каждом уравнении есть ровно одна единица, так что оно выполняется. Легко выполнить и обратное построение (гамильтонова пути по решению системы уравнений).

Как избавиться от парных рёбер. Осталось свести задачу о гамильтоновом цикле с парными рёбрами к обычной задаче о гамильтоновом цикле, то есть как-то избавиться от парных рёбер (сделать множество C пустым).

Рис. 8.11. Сведение УНЕ к гамильтонову циклу с парными рёбрами.

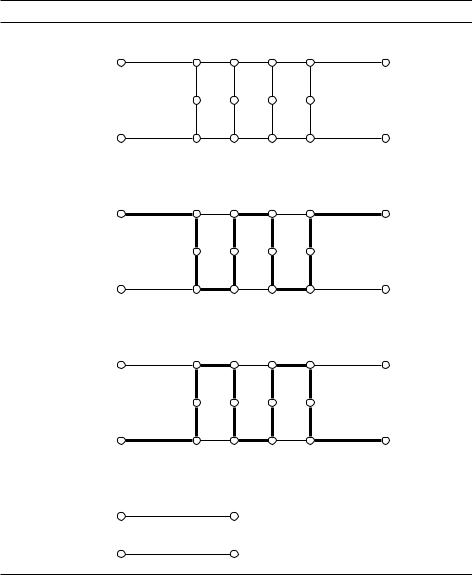
DRAFTЭто делается с помощью блоков, изображённых на рис. 8.12. Пусть этот блок является частью какого-то графа G, соединённой с другими вершинами лишь в точках a, b, c, d. Давайте покажем, что гамильтонов цикл в графе G может проходить блок лишь двумя способами, изображёнными жирными линиями. Ясно, что вертикальные линии неизбежны, иначе мы не посетим средний ряд вершин. Посмотрим на одну из них (не крайнюю): пройдя по ней, цикл должен повернуть налево или направо, и из рисунка видно, что этот выбор определяет всё дальнейшее (и всё предшествующее) поведение: мы попадаем на следующую вертикальную линию, которая продолжает цикл, и следующий выбор однозначен (иначе получится замкнутый круг).

Таким образом, эта конструкция ведёт себя точно так же, как два ребра fa, bg и fc, dg, объединённые в пару (рис. 8.12(d)), в варианте задачи с парными рёбрами.

Теперь понятно, как свести задачу о гамильтоновом цикле с парными рёбрами к задаче об обычном гамильтоновом цикле. Будем постепенно уменьшать количество пар, пока они все не исчезнут. Взяв какую-то пару рёбер (fa, bg, fc, dg) 2 C, мы заменяем эту пару на конструкцию рис. 8.12(a). Но надо иметь в виду, что рёбра fa, bg или fc, dg могли входить и в другие пары. Ничего страшного: во всех оставшихся парах, содержащих ребро fa, bg, заменяем его на ребро fa, f g из только что добавленной конструкции (прохождение по нему кодирует прохождение по ребру fa, bg исходного графа). Аналогично заменяем fc, dg (в других парах) на fc, hg. Такое преобразование графа полиномиально, поскольку на каждую пару рёбер добавляется по

12 вершин. Легко видеть, что гамильтоновы циклы в полученном графе находятся во взаимно однозначном соответствии с гамильтоновыми циклами в исходном графе, согласованными с множеством пар рёбер C.

Гамильтонов цикл ! коммивояжёр

По данному графу G = (V, E) построим следующий граф для задачи коммивояжёра: множество городов совпадает с jV j; расстояние между городами u и v положим равным 1, если fu, vg 2 E, и 1 + в противном случае. Значение

¾ 1 мы подберём позже. В полученном графе будем искать цикл суммарного веса не более jV j.

Ясно, что если в исходном графе есть гамильтонов цикл, то и в полученном графе есть гамильтонов цикл веса ровно jV j. Если же гамильтонова цикла в исходном графе нет, то любой гамильтонов цикл в полученном графе будет иметь вес хотя бы jV j + (ему придётся хотя бы раз пройти по ребру веса 1 + , а все остальные jV j 1 рёбер имеют вес хотя бы 1). Итак, мы свели задачу о гамильтоновом цикле к задаче коммивояжёра.

Зачем, однако, мы ввели параметр ? Ведь для сведения достаточно было

DRAFT

бы взять, скажем, =1. При =1 веса рёбер в построенном графе удовлетворяют неравенству треугольника: для городов i, j, k выполняется неравенство di j + djk ¾ dik (действительно, di j + djk ¾ 1 + 1 = 2 ¾ dik). Таким образом, мы свели задачу о гамильтоновом цикле к задаче коммивояжёра с дополнительным ограничением (расстояния удовлетворяют неравенству треугольника). Этот частный случай часто возникает на практике и в некотором смысле проще общего случая: для него есть эффективные приближённые алгоритмы.

Если же взять большее значение , то веса рёбер уже не будут удовлетворять неравенству треугольника, но зато наше сведение будет обладать другим интересным свойством. А именно, в полученном графе либо есть гамильтонов цикл веса jV j, либо любой гамильтонов цикл имеет вес как минимум jV j + , и это число может быть сильно больше jV j. В главе 9 мы увидим, что такой зазор позволяет показать, что (в предположении P 6= NP) для общей задачи коммивояжёра нет эффективных приближённых алгоритмов.

Любая задача класса NP ! выполнимость

Мы свели задачу о выполнимости к разным задачам из схемы на рис. 8.7. Сейчас мы замкнём круг и убедимся, что верно и обратное, установив, что все они –– и вообще любые задачи поиска (= задачи из NP) –– сводятся к задаче выполнимости. Тем самым мы докажем, что все задачи на рис. 8.7 эквивалентны друг другу и NP-полны.

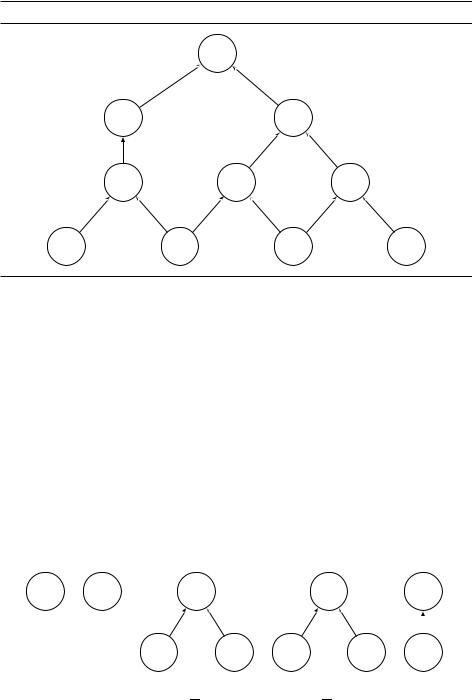
Мы сведём произвольную задачу из NP к чуть более общему варианту задачи о выполнимости –– задаче выполнимости булевой схемы (circuit SAT). Входом данной задачи является булева схема (см. рис. 8.13 и раздел 7.7), то есть ациклический ориентированный граф, в котором есть вершины следующих типов:

ff Элементы AND и OR, имеющие входящую степень 2. ff Элементы NOT, имеющие входящую степень 1.

ff Известные входы (входящая степень ноль), помеченные константой true

или false.

ff Неизвестные входы (входящая степень 0), помеченные знаком «?».

Одна из вершин схемы имеет выходную степень 0 и помечена как «выход». Выбрав значения для неизвестных входов, мы можем определить значе-

ние в каждой вершине (в том числе и в выходной вершине), пользуясь законами булевой логики (типа false _ true = true). Например, при подстановке значений true, false, true схема рис. 8.13 вычисляет значение false.

Рис. 8.13. Вход для задачи выполнимости булевой схемы.

Задача о выполнимости булевой схемы возникает, когда задана булева схема, а найти нужно набор значений неизвестных, при котором на выходе схемы будет true (или же сообщить, что такого набора нет). Например, набор (false, true, true) выполняет схему рис. 8.13.

Эта задача обобщает рассмотренную раньше задачу о выполнимости, ведь формулу в КНФ легко задать схемой. Такая схема будет вычислять конъюнкцию дизъюнктов (с помощью нескольких элементов типа AND), а каждый дизъюнкт будет дизъюнкцией литералов. Наконец, литерал –– это либо неизвестный вход, либо его отрицание. (Известные входы при этом не нужны.)

Это обобщение не является принципиальным: сейчас мы сведём задачу о выполнимости булевой схемы к задаче выполнимости, заменив схему на формулу в КНФ. В ней появятся новые переменные (кроме входных неизвестных): для каждой вершины заведём новую переменную g и запишем следующие дизъюнкты, гарантирующие, что значение этой переменной действи-

(Понятно ли, почему достаточно записать такие дизъюнкты?) Чтобы заставить схему вычислять значение true, добавим также дизъюнкт (g) для выходного элемента g. Выполняющие наборы для полученной формулы в КНФ находятся во взаимно однозначном соответствии с выполняющими наборами исходной схемы.

Вернёмся теперь к нашей основной задаче –– сведению произвольной задачи поиска A к задаче выполнимости булевой схемы. Как построить такое сведение? Кажется, это будет непросто, ведь мы ничего не знаем об A, кроме того, что она является задачей поиска.

DRAFTЗначит, воспользоваться нужно именно этим. Как мы помним, задача поиска задаётся проверяющим алгоритмом. Именно, для A есть алгоритм C , проверяющий по входу I и кандидату S, действительно ли S является решением. Более того, этот алгоритм осуществляет такую проверку за полиномиальное от длины I время (из чего, в частности, следует, что длина S должна быть ограничена полиномом от длины I, иначе мы не успеем даже прочесть S).

Вспомним теперь наше рассуждение из раздела 7.7 о том, что по полиномиальному алгоритму можно построить полиномиальную схему, которая (для входов данной длины) будет вычислять то же самое, что и алгоритм. В нашем случае алгоритм C отвечает на вопрос, является ли S решением для I. Этот ответ появится на выходе схемы.

Итак, по входу I задачи A мы за полиномиальное время можем построить схему, известными входными элементами которой будут биты I, а неизвестными –– биты S. На выходе такой схемы появится значение true тогда и только тогда, когда на неизвестные входы поданы биты, кодирующие решение S

для I. Другими словами, выполняющие наборы для схемы соответствуют решениям задачи A для входа I, что нам и требовалось. Сведение построено.

Неразрешимые задачи

Задача из класса NP может быть решена экспоненциальным алгоритмом, который просто перебирает всех потенциальных кандидатов (напомним, что их размер ограничен полиномом от размера входа). Оказывается, что бывают задачи, которые не решаются вообще никаким алгоритмом (ни полиномиальным, ни экспоненциальным, ни ещё более долго работающим); их называют неразрешимыми (unsolvable).

Например, таков арифметический вариант задачи выполнимости. В нём по заданному алгебраическому уравнению типа

x3 yz + 2 y4z2 7x y5z = 6

(в левой части стоит многочлен от нескольких переменных с целыми коэффициентами) нужно определить, есть ли у него целочисленные решения.

Неразрешимость этой конкретной задачи была доказана в 1970 году (в результате работ Джулии Робинсон, Мартина Дэвиса, Хилари Патнэма и Юрия Матиясевича), но впервые неразрешимая задача была указана Аланом Тьюрингом в 1936 году; он был тогда студентом математического фа-

260 Глава 8. NP-полные задачи

культета в Кембридже (Англия). В те времена ещё не было ни компьютеров, ни языков программирования (скорее наоборот, компьютеры и языки программирования появились благодаря Тьюрингу). На современном языке эту задачу можно описать так.

Допустим, нам дана программа на некотором языке программирования, а также вход этой программы. Мы хотим понять, остановится ли программа, начав работать на этом входе. Было бы очень здорово иметь процедуру Terminates(p, x), которая по программе p и файлу с данными x отвечала

DRAFTбы на вопрос, остановится ли программа p на данных x.

Но как можно было бы реализовать такую процедуру? Если вы не встречались с этой задачей раньше, попробуйте прикинуть, как можно было бы определить, зациклится ли данная программа на данном входе или нет.

На самом деле такую процедуру написать нельзя. Докажем это от противного. Пусть такая процедура Terminates(p, x) есть. Напишем тогда такую процедуру с одним параметром:

процедура Paradox(z)

повторять пока Terminates(z, z) истинно

Она останавливается на входе z тогда и только тогда, когда процедура z не останавливается, если ей на вход дать её собственный код (z).

Наверно, вы уже видите подвох. Давайте создадим файл Paradox с кодом этой процедуры и выполним вызов Paradox(Paradox). Остановится он или нет? Оба ответа на этот вопрос –– положительный и отрицательный –– приводят к противоречию. Противоречие произошло из-за того, что мы предположили существование процедуры, проверяющей остановку. Так что такой процедуры нет: как говорят, проблема останова (halting problem) неразрешима.

Из этого можно сделать вывод, что в программировании можно автоматизировать далеко не всё. Мы видели, что нельзя написать процедуру, определяющую, зацикливается ли программа на данном входе. Может быть, можно хотя бы проверить, не случится ли переполнение буфера во время исполнения программы? Тоже нет (к этой задаче сводится проблема останова –– понятно, как?) Программирование всегда будет требовать дисциплины, изобретательности и остроумия.

Упражнения

8.1. Задачи поиска и задачи оптимизации. Для задачи коммивояжёра варианты с поиском и с оптимизацией выглядят так:

Задача поиска:

Вход: матрица расстояний, бюджет b.

Выход: цикл веса не более b, проходящий по всем вершинам графа, если такой цикл есть.