
Дасгупты, Пападимитриу, Вазирани «Алгоритмы»
.pdf
8.1. Задачи поиска |
231 |
временных терминах, что экспоненциально растущее (он называл это «геометрическим ростом») население неизбежно сталкивается с полиномиально ограниченными ресурсами (идея, позже повлиявшая на Дарвина).
В 1965 году Гордон Мур, один из первых разработчиков микросхем, заметил, что количество транзисторов в микросхеме в 60-х годах удваивалось примерно каждый год. Мур предположил, что так и будет продолжаться. Сейчас «закон Мура» обычно формулируют так: быстродействие компьютера удваивается каждые 18 месяцев. И действительно, это происходит уже
DRAFTлет сорок –– и наряду с разработкой эффективных алгоритмов стало основой стремительного развития информационных технологий.
На первый взгляд кажется, что закон Мура делает ненужными полиномиальные алгоритмы: пусть даже время работы алгоритма экспоненциально велико, почему бы просто не подождать, пока компьютеры станут достаточно быстрыми? На самом деле наоборот: рост быстродействия важен именно потому, что мы используем полиномиальные алгоритмы.
Для примера рассмотрим алгоритм, решающий задачу выполнимости за время O(2n). В 1975 году такой алгоритм за час мог бы решить задачу для 25 переменных, в 1983 –– для 31, в 1995 –– для 38. Наконец, на современных компьютерах этот алгоритм за час смог бы обрабатывать формулы с 45 переменными. Прогресс налицо, да только появление новой переменной (удвоение числа операций) требует полутора лет ожидания, а размеры формул в приложениях (в том числе используемых при разработке процессоров) растут гораздо быстрее.
А вот для алгоритма с асимптотикой O(n) или O(n log n) допустимый размер входов увеличивается примерно в 100 раз каждые 10 лет, для алгоритма со временем работы O(n2) –– в 10 раз. Даже не особо эффективный алгоритм с оценкой O(n6) позволит за это время удвоить размер решаемых задач. Можно сказать так: экспоненциальный рост скорости процессоров приводит к полиномиальному росту размера задач в случае экспоненциальных алгоритмов, и к экспоненциальному росту размера задач для полиномиальных алгоритмов. Так что воспользоваться законом Мура мы смогли именно благодаря эффективным алгоритмам.
Как понимали и Сисса, и Мальтус, и Мур, экспоненциальному росту рано или поздно приходит конец –– бактерии останутся без еды, а микросхемы упрутся в атомный масштаб, закону Мура осталось десять или двадцать лет. Дальше будут нужны новые алгоритмы или же совсем новые идеи –– скажем, квантовые вычисления, о которых пойдёт речь в главе 10.
решаются за полиномиальное время). Сейчас же настало время познакомиться с задачами, для которых эффективного решения до сих пор не известно. В них тоже надо найти объект с некоторыми свойствами среди экспоненциально большого множества кандидатов –– но для них никто не знает, как избежать перебора: самые быстрые известные алгоритмы для таких задач имеют экспоненциальное время работы.

8.1. Задачи поиска |
|
|
233 |
Несмотря на усилия множества исследователей в течение последних пя- |
|||
тидесяти лет, все известные алгоритмы для задачи выполнимости имеют экс- |
|||
поненциальное (в худшем случае) время работы. С другой стороны, для двух |
|||
её естественных частных случаев известны эффективные (полиномиальные) |
|||
алгоритмы. |
|
|
|
(1) Если каждый дизъюнкт содержит не более одного положительного ли- |
|||
терала, то формула называется хорновской и её выполнимость может быть |
|||
проверена простым жадным алгоритмом из раздела 5.3. |
|||
(2) Если все дизъюнкты содержат не более двух литералов, то помогает |
|||
теория графов: задачу можно решить при помощи поиска компонент силь- |
|||
ной связности в специальном графе, построенном по входной формуле (уп- |
|||
ражнение 3.28). Ещё один алгоритм для этого частного случая см. в главе 9. |
|||
Но чуть ослабив ограничения и разрешив каждому дизъюнкту содержать |
|||
до трёх литералов (как в примере выше), мы опять получаем трудную задачу! |
|||
Задача коммивояжёра |
|
|
|
В задаче коммивояжёра (traveling salesman problem, TSP) даны n вершин 1, |
|||
, n и все n(n 1)=2 расстояний между ними, а также некоторый бюджет b. |
|||
Найти необходимо маршрут, то есть цикл, который проходит по каждой |
|||
вершине графа ровно один раз, общей стоимостью не более b (или же со- |
|||
общить, что такого цикла нет). Другими словами, мы ищем перестановку |
|||
(1), , (n) вершин, для которой длина обхода в этом порядке не превос- |
|||
ходит b: |
|
|
|
d (1), (2) + d (2), (3) + + d (n), (1) ¶ b. |
|||
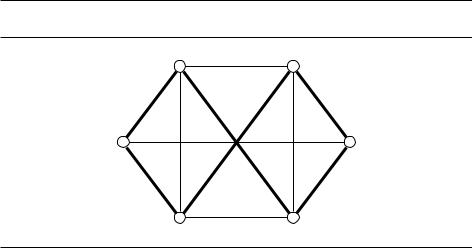
Пример приведён на рис. 8.1 (нарисованы не все рёбра; считаем, что осталь- |
|||
ные длины очень велики). |
|
|
|
Рис. 8.1. Оптимальный маршрут коммивояжёра, выделенный жирным, имеет дли- |
|||
ну 16. |
|
|
|
|
|
5 |
|
3 |
2 |
3 |
3 |
|
|
|
4 |
1 |
|
|
|
3 |
4 |
|
2 |
|
|
||
DRAFT |
|||
|
|
6 |
|


8.1. Задачи поиска |
235 |
рами –– соединяющие их мосты:
северный берег
малый остров 
 большой остров DRAFTвестно. южный берег
большой остров DRAFTвестно. южный берег
В графе есть кратные рёбра, отвечающие за разные мосты между двумя вершинами. Мы хотим найти путь, который проходит по всем рёбрам ровно по одному разу (путь может проходить через некоторые вершины больше одного раза). Другими словами, нас интересует, можно ли нарисовать граф, не отрывая пера от бумаги.
Эйлер придумал простой и изящный ответ на этот вопрос: необходимо и достаточно, чтобы граф был связен и чтобы степень всех вершин, кроме, возможно, двух (начала и конца пути), была чётна (упражнение 3.26). Это объясняет, почему нельзя обойти все мосты Кёнигсберга по одному разу: степени всех четырёх вершин нечётны.
В терминах задач поиска: входом задачи об эйлеровом пути (Euler path) является граф, а решением –– путь, проходящий по каждому ребру ровно по одному разу. Из критерия Эйлера следует, что эта задача может быть решена за полиномиальное время (рассуждение Эйлера указывает искомый путь).
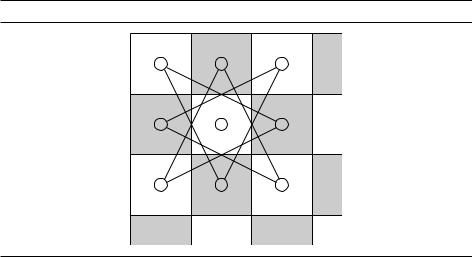
Почти за тысячу лет до этого кашмирский поэт по имени Рудрата задал следующий вопрос: можно ли ходом коня обойти все клетки шахматной доски, побывав в каждой клетке ровно один раз, и вернуться в исходную клетку? Снова получаем задачу на графе: в нём 64 вершины (клетки); две клетки соединены ребром, если за один ход конём можно из одной попасть в другую (в таком случае координаты этих двух клеток по одному направлению различаются на 2, а по другому –– на 1). На рис. 8.2 показана часть графа, соответствующая левому верхнему углу доски. Можете ли вы найти искомый маршрут?
Как видите, здесь требуется обойти по разу все вершины графа, а не все рёбра как в задаче Эйлера. Аналогичный вопрос может быть поставлен не только для шахматной доски, но и для любого графа. Получаем задачу о гамильтоновом цикле: найти в данном графе цикл, проходящий через все вершины графа по одному разу, или сообщить, что такого нет.1 Задача очень похожа на задачу коммивояжёра, и полиномиальных алгоритмов для неё неиз-
1В оригинале книги авторы называют данную задачу задачей Рудраты и замечают, что её
вXIX веке переоткрыл ирландский математик Гамильтон –– тот самый, в честь которого названы гамильтонианы в физике. В русском переводе сохранено традиционное название –– задача о гамильтоновом цикле. –– Прим. перев.
236 |
Глава 8. NP-полные задачи |
Рис. 8.2. Ходы коня в углу доски.
DRAFTВ задаче о эйлеровом пути необходимо обойти все рёбра, в то время как в задаче о гамильтоновом цикле нужно обойти все вершины. Но есть ещё и другое различие: в первой мы ищем путь, а во второй –– цикл. Это, однако, не принципиально: можно искать гамильтонов путь, проходящий все вершины по одному разу, и эта задача так же сложна, как и задача о цикле (см. ниже).
Разрезы и бисекции
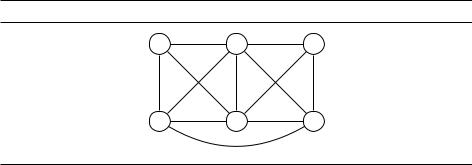
Разрезом (cut) называется множество рёбер, при выкидывании которого граф теряет связность. В задаче о минимальном разрезе (minimum cut) по данному графу и бюджету b необходимо найти разрез из b (или меньше) рёбер. Например, минимальный разрез графа рис. 8.3 имеет вес 3. Эту задачу можно решить, вычислив максимальный поток n 1 раз: присвоим каждому ребру графа пропускную способность 1, зафиксируем какую-нибудь вершину графа и найдём максимальный поток из этой вершины до каждой из оставшихся вершин. Минимальная величина этих потоков будет равна (по теореме о максимальном потоке и минимальном разрезе) минимальному разрезу. (Мы видели совсем другой вероятностный алгоритм для этой задачи на с. 137.)
Для многих графов (в том числе графа рис. 8.3) минимальный разрез отсоединяет от графа одну вершину (состоит из всех рёбер, инцидентных ка- кой-то вершине графа). Более интересны разрезы, которые разделяют вершины графа на две сопоставимые по размеру части. В задаче о сбалансированном разрезе (balanced cut) по данному графу с n вершинами и бюджету b необходимо найти разбиение вершин графа на два множества S и T , для которого jSj, jT j ¾ n=3 и множества S и T соединены не более чем b рёбрами. Очередная трудная задача...
Вот пример практической ситуации, где полезны сбалансированные разрезы. Пусть на картинке нужно выделить объекты (скажем, отделить слона от
8.1. Задачи поиска |
237 |
Рис. 8.3. Каков минимальный разрез в этом графе?
DRAFTзелёной травы и синего неба). Построим граф, где каждому пикселю изображения будет соответствовать вершина и где два пикселя соединены ребром, если они расположены рядом и имеют похожие цвета. Тогда отдельному объекту картинки (слону, например) будет соответствовать множество сильно связанных друг с другом (и слабо связанных с остальной частью) вершин. Минимальный сбалансированный разрез разделит вершины на два кластера, не разрезав объекты –– скажем, сначала он может отделить слона от неба и травы, а последующий разрез второй части разделит небо и траву. Подобные задачи называют кластеризацией.
Целочисленное линейное программирование
Как мы уже видели в главе 7, симплекс-метод не полиномиален по времени, но известны и полиномиальные алгоритмы решения задач линейного программирования, так что эта задача эффективно решается и в теории, и на практике. Хуже обстоит дело, если нас интересуют только целые значения переменных. Эта задача называется задачей целочисленного линейного программирования (ЦЛП; integer linear programming, ILP). В виде задачи поиска она выглядит так: дано множество линейных неравенств Ax ¶ b, где A –– матрица размера m n, а b –– вектор длины m; кроме того, дана целевая функция, заданная вектором c размера n, а также цель g (аналог бюджета в максимизационных задачах). Необходимо найти неотрицательный целочисленный вектор x длины n, для которого Ax ¶ b и c x ¾ g.
Как видно, нужно найти вектор, удовлетворяющий некоторым линейным неравенствам (в нашей формулировке ограничение c x ¾ g можно присоединить к системе неравенств Ax ¶ b). Таким образом, по данным A и b нужно найти вектор x, для которого Ax ¶b, или же сообщить, что такого нет. Эффективный алгоритм для такой задачи был бы чрезвычайно полезен на практике, но такой алгоритм до сих пор не придумали.
Есть также очень специальный случай этой задачи, который уже труден: необходимо найти вектор x, состоящий только из нулей и единиц, для которого Ax = 1, где A –– матрица размера m n, состоящая из нулей и единиц, а 1 –– вектор длины m из одних единиц. Это действительно частный случай (см. раздел 7.1.4); назовём его задачей об уравнениях в нулях и единицах (УНЕ; zero-one equations, ZOE).
238 |
Глава 8. NP-полные задачи |
Мы привели несколько примеров задач поиска: одни решаются за полиномиальное время, а другие, хотя и похожие, до сих пор такому решению не поддаются. Мы приведём ещё несколько задач, которые нам понадобятся дальше, при сравнении сложности задач; нетерпеливые читатели могут пока это пропустить и перейти к разделу 8.2 (и возвращаться, когда эти задачи будут упоминаться).
Трёхдольное сочетание
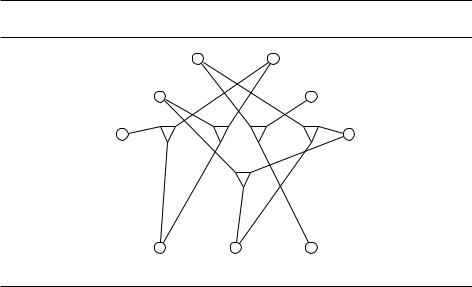
Вспомним задачу о паросочетании в двудольном графе: дан двудольный граф с долями размера n (условно говоря, n мальчиков и n девочек); требуется найти n рёбер, не имеющих общих вершин, или сообщить, что таких нет. В разделе 7.3 мы видели, как решить эту задачу, сведя её к задаче о максимальном потоке. Но для более общей задачи трёхдольного сочетания (3D Matching) полиномиальный алгоритм придумать не удаётся. В новой постановке кроме n мальчиков и n девочек есть ещё и n домашних животных, а вместо рёбер задаются тройки, состоящие из мальчика, девочки и животного. Тройка (b, g, p) означает, что мальчик b, девочка g и животное p уживутся друг с другом. Мы хотим найти n непересекающихся троек, создав тем самым n счастливых «семей».
Видите ли вы решение на рис. 8.4?
Рис. 8.4. Пример задачи о трёхдольном сочетании. Треугольники обозначают допустимые варианты.
Владимир |
Вера |
Борис |
Надежда |
Андрей |
Любовь |
кошка |
собака канарейка |
Независимое множество, вершинное покрытие и клика |
|
DRAFT |
|
В задаче о независимом множестве (independent set problem), которую мы уже |
|
рассматривали в разделе 6.7, на вход даётся граф и число g, а найти необходимо g вершин, никакие две из которых не соединены ребром. Можете ли

8.1. Задачи поиска |
239 |
вы найти три такие вершины в графе на рис. 8.5? А четыре? Из раздела 6.7 мы знаем, что для дерева эта задача простая –– но для произвольных графов полиномиальный алгоритм неизвестен.
Рис. 8.5. Каково максимальное независимое множество в этом графе?
DRAFTЕсть много других задач поиска для графов. В задаче о вершинном покрытии (vertex cover problem) для данного графа и числа b требуется найти b вершин, которые «задевают» каждое ребро (для любого ребра графа хотя бы один из концов ребра лежит в этом множестве). Можете ли вы покрыть все рёбра графа рис. 8.5 семью вершинами? А шестью? Как связана эта задача с задачей о независимом множестве?
Задача о вершинном покрытии (vertex cover problem) является частным случаем задачи о покрытии множествами (см. главу 5). В задаче о покрытии множествами на вход даются множество E и несколько его подмножеств S1, , Sm, а также число b. Найти необходимо b из заданных подмножеств, объединение которых покрывает E. (Как свести задачу о трёхдольном сочетании к задаче о покрытии множествами?)
В задаче о вершинном покрытии элементами E являются рёбра графа, а для каждой вершины графа есть множество Si , содержащее все смежные с ней рёбра.
Наконец, в задаче о клике (clique problem) по данному графу и числу g необходимо найти множество из g вершин, каждые две из которых соединены ребром. Каков размер максимальной клики в графе на рис. 8.5? Как задача о клике связана с задачей о независимом множестве?
Максимальный путь
Мы уже знаем, что задача о кратчайшем пути в графе решается эффективно. А что можно сказать про задачу о максимальном пути (longest path problem)?
240 |
Глава 8. NP-полные задачи |
В ней дан граф G с неотрицательными весами на рёбрах и двумя выделенными вершинами s и t, а также число g. Найти необходимо путь из s в t суммарного веса не меньше g. Естественно, мы предполагаем, что путь должен быть простым (не заходить дважды в одну и ту же вершину).
Эффективных алгоритмов для этой задачи (которой могли бы заинтересоваться жулики-таксисты) тоже пока не нашли.
Рюкзак и сумма подмножества
DRAFTВспомним задачу о рюкзаке (knapsack problem), уже рассмотренную нами в разделе 6.4. В ней заданы целочисленные веса w1, , wn и стоимости v1, , vn для n предметов. Также задана граница W для веса и цель g (первый параметр есть в исходной оптимизационной задаче, второй параметр добавлен для того, чтобы получить задачу поиска). Необходимо выбрать несколько предметов так, чтобы их суммарный вес не превышал W и чтобы в то же время их суммарная стоимость была не меньше g. Как обычно, если такой возможности нет, требуется сообщить об этом.
С помощью динамического программирования в разделе 6.4 мы разработали алгоритм для задачи о рюкзаке со временем работы O(nW ). Мы отмечали, что это экспоненциальное время работы, потому что в качестве множителя оно включает W , а не log W (размер двоичной записи числа W ). Есть и другой алгоритм с экспоненциальным временем работы: просто переберём все 2n возможных вариантов выбора. А вот существует ли для этой задачи полиномиальный алгоритм, неизвестно.
Рассмотрим теперь вариант задачи о рюкзаке, в котором числа на вход даются в унарной системе счисления: например, число 12 запишется как I I I I I I I I I I I I. Ясно, что неразумно записывать числа таким образом, но тем не менее мы имеем полное право определить такую задачу поиска, которую будем называть унарной задачей о рюкзаке (unary knapsack problem). Мы уже знаем, что эта (искусственная) задача решается за полиномиальное время.
А вот ещё один вариант: пусть вес каждого предмета равен его стоимости (и все числа даны в двоичной системе счисления), а также g = W . Продолжая историю с вором, здесь можно сказать, что все предметы представляют собой золотые слитки (разного веса) и вор хочет забить ими свой рюкзак под завязку. Ясно, что в этой задаче нам просто надо найти в данном множестве (или даже мультимножестве, если есть повторяющиеся числа) подмножество с суммой W . Это частный случай задачи о рюкзаке –– быть может, хотя бы для него есть полиномиальный алгоритм? Оказывается, что эта задача, называемая задачей о сумме подмножества (subset sum problem), тоже очень трудна.
Но раз уж задача о сумме подмножества не проще общей задачи о рюкзаке, почему этот специальный случай интересен? Потому что он просто формулируется, и когда мы будем сводить задачи поиска друг к другу, такие простые эталонные задачи, как задача о сумме подмножества и задача 3-выпол- нимости, будут очень полезны.
