Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

Рис. 4.16. Операции с двоичной кучей.

процедура Insert(h, x)

BubbleUp(h, x, jhj + 1)

процедура DecreaseKey(h, x) BubbleUp(h, x, h 1(x))

DRAFTфункция DeleteMin(h)

если jhj = 0:

вернуть null

иначе:

x h[1]

SiftDown(h, h[jhj], 1)

вернуть x

функция MakeHeap(S)

h пустой массив размера jSj для x 2 S:

h[jhj + 1] x

для i от jSj до 1:

SiftDown(h, h[i], i)

вернуть h

процедура BubbleUp(h, x, i)

{помещает элемент x в позицию i массива h и даёт ему «всплыть»}

p di=2e

пока i 6= 1 и key(h[p]) > key(x):

c MinChild(h, i)

пока c 6= 0 и key(h[c]) > key(x):

h[i] h[c]; i c; c MinChild(h, i) h[i] x

функция MinChild(h, i)

если 2i > jhj:

вернуть 0 {нет детей} иначе:

вернуть arg minfkey(h[j]): 2i ¶ j ¶ minfjhj, 2i + 1gg

Последнего легко добиться, поддерживая значения h 1 во вспомогательном массиве.

(c) Покажите, что время работы процедуры MakeHeap на множестве из n элементов есть O(n). Для какого множества время работы будет наихудшим? (Подсказка: для начала покажите, что время работы не превосходит

n

P log(n=i).)

i=1

(d) Что надо изменить, чтобы хранить d-ичные кучи?

DRAFTПостройте эффективный алгоритм, который по данному графу с положительными весами и по данной вершине s заполняет массив best.

4.17. Допустим, что нам нужно найти кратчайшие расстояния от данной вершины в графе с весами рёбер в интервале 0, 1, ‌, W , где W –– сравнительно небольшое число.

(a) Покажите, что тогда алгоритм Дейкстры можно модифицировать, по-

лучив время работы O(W jV j + jEj).

(b) Постройте другой вариант алгоритма с оценкой O((jV j + jEj) log W ).

4.18. Если в графе с различными длинами рёбер есть несколько кратчайших путей между двумя вершинами, часто выбирают тот, в котором меньше рёбер. Например, если вершины обозначают города, а веса рёбер –– стоимость перелёта, то из нескольких одинаково дорогих вариантов удобнее маршрут с наименьшим количеством пересадок. С учётом этого зададим массив best следующим образом:

best[u] = минимальное число рёбер на кратчайшем пути из s в u.

Например, для графа на рисунке значениями массива best для вершин

S, A, B, C, D, E, F будут 0, 1, 1, 1, 2, 2, 3 (соответственно).

4.19. Обобщённая задача о кратчайших путях. При маршрутизации пакетов в сети задержки есть не только на линиях, но и в узлах (маршрутизаторах). Поэтому разумно рассмотреть обобщение задачи о кратчайших путях.

Пусть для графа заданы не только длины рёбер fle : e 2 Eg, но и стоимости вершин fcv : v 2 V g. Определим стоимость пути как сумму длин его рёбер и стоимости всех его вершин. Постройте эффективный алгоритм для следующей задачи.

Вход: ориентированный граф G = (V, E); положительные длины рёбер le и стоимости вершин cv ; начальная вершина s 2 V .

Выход: массив cost, в котором для каждой вершины u значение cost[u] есть минимальная стоимость пути из s в u.

Отметим, что cost[s] = cs.

4.20. Пусть граф G = (V, E) представляет собой множество городов V и множество дорог E между ними. У каждой дороги e 2 E есть длина le. Решено построить новую дорогу, и список E0 содержит пары вершин, между которыми новая дорога может быть построена. Для всех возможных новых дорог e0 2 E0

известна длина l . Надо найти дорогу из E0, строительство которой приведёт

DRAFTe0

к максимальному уменьшению длины кратчайшего пути между заданными

двумя городами s и t в G. Постройте эффективный алгоритм для такой задачи.

4.21. Применения задачи о кратчайших путях можно найти даже в валют-

ных операциях. Пусть через c1, c2, ‌, cn обозначены различные валюты. Например, c1 может обозначать рубли, c2 –– доллары, c3 –– фунты. Пусть через ri, j обозначен курс конвертации валюты ci в cj : на одну единицу валюты ci можно купить ri, j единиц валюты cj . Данные курсы удовлетворяют естественному условию ri, j rj,i < 1, которое говорит, что обмен туда-обратно невыгоден.

(a) Постройте эффективный алгоритм, который, зная все ri, j , находит наиболее выгодную последовательность обменов для конвертации заданной ва-

люты s в заданную валюту t. (Подсказка: для решения задачи представьте входные данные в виде графа с вещественными весами.)

Под влиянием спроса и предложения курсы валют меняются. Представим, что в какой-то момент нашлись валюты ci , ci , ‌, ci , для которых ri ,i ri ,i ‌ri ,i ri ,i > 1. Это означает, что обменяв1 2 какоеk-то количество валюты1 2 2 3 в kсоответствии1 k k 1 с данной последовательностью, мы в итоге полу-

ci

чим больше1 исходного. (Вряд ли это продлится долго, но обидно упустить

такую возможность!)

(b) Постройте эффективный алгоритм, проверяющий наличие такой аномальной ситуации. (Подсказка: используйте граф предыдущего пункта.)

4.22. Задача о путешествующем пароходе. Представьте, что у вас есть пароход, который может совершать рейсы между портовыми городами из множества V . Посещая город i, вы зарабатываете pi рублей, а стоимость перемещения из города i в город j составляет ci j > 0 рублей. Вы хотите найти циклический маршрут, максимизирующий отношение прибыли к затратам.

Для этого рассмотрим ориентированный граф G = (V, E), где вершинами являются города и каждые две вершины соединены ребром. Определим относительную прибыль цикла C следующим образом:

P

pj r(C) = (i, j)2C .

P

ci j

(i, j)2C

Через r обозначим максимальную относительную прибыль простого цикла. Значение r можно найти двоичным поиском, если мы умеем проверять по данному r, верно ли неравенство r > r .

Глава 5

Жадные алгоритмы

DRAFTЯсно, что оптимальный набор рёбер не может содержать циклов, потому что удаление ребра из цикла снижает стоимость без потери связности:

Хороший шахматист просматривает варианты на много ходов вперёд и легко выиграет у новичка, который думает только о ближайших последствиях. В других играх разница не так заметна; например, можно неплохо играть в «Эрудит», думая только о ближайшем ходе. Это же относится к алгоритмическим задачам: бывают ситуации, в которых жадный (greedy) алгоритм, стремящийся максимизировать выгоду (в том или ином смысле) каждого отдельного шага, приводит к оптимальному решению. Таким случаям и посвящена эта глава. Наш первый пример –– минимальные покрывающие (остовные) деревья.

5.1. Покрывающие деревья

Мы хотим связать несколько компьютеров в сеть, соединяя их попарно. Это соответствует задаче на графе, где вершины –– компьютеры, (неориентированные) рёбра –– возможные связи, и надо получить связный граф. Для каждого соединения известна стоимость обслуживания (неотрицательный вес соответствующего ребра). Как найти самый дешёвый вариант?

Свойство 1. Удаление ребра из цикла сохраняет связность графа.

Поэтому решением должен быть связный ациклический граф; неориентированные графы такого вида называются деревьями. Необходимое нам дерево с минимальным суммарным весом называется минимальным покрывающим деревом (minimum spanning tree, MST). Формально говоря, наша задача такова:

Вход: неориентированный граф G = (V, E), неотрицательные веса рёбер we.

Выход: дерево T = (V, E0), где E0 E, минимизирующее

X

weight(T ) = we.

e2E0

В предыдущем примере минимальное покрывающее дерево имеет стоимость 16:

DRAFTДеревья

Дерево –– это неориентированный связный ациклический граф.

Свойство 2. Дерево с n вершинами содержит n 1 ребро.

В самом деле, будем строить дерево, начав с пустого графа и добавляя рёбра по одному. Изначально каждая из n вершин образует компоненту связности. При добавлении ребра две компоненты сливаются (ребро не может соединять две вершины одной компоненты –– будет цикл). В итоге остаётся одна компонента, так что понадобится n 1 шагов.

Верно и обратное:

Свойство 3. Всякий связный неориентированный граф G = (V, E), где jEj = jV j 1, является деревом.

Надо показать, что в G нет циклов. Если есть цикл, по свойству 1 можно удалить одно из его рёбер, не нарушая связности (и не меняя числа вершин). Когда циклов не останется, будет дерево, значит, рёбер по-прежнему jV j 1, что невозможно, если мы их удаляли.

Иначе говоря, мы можем определить, является ли связный граф деревом, просто сосчитав, сколько в нем рёбер.

Свойство 4. Неориентированный граф является деревом тогда и только тогда, когда между любыми двумя вершинами существует ровно один путь.

(Имеются в виду пути, не проходящие по ребру туда-обратно.) Если в дереве есть два пути между одними и теми же вершинами, то в некоторый момент первый путь отклоняется от второго и после этого в какой-то момент снова с ним пересекается. При этом образуется цикл. С другой стороны, если в графе между любыми двумя вершинами имеется путь, то граф связен. Если этот путь единственен, то циклов нет (в цикле между любыми двумя вершинами есть два пути).

5.1.1. Жадная стратегия

Алгоритм Крускала (Kruskal) поиска минимального покрывающего дерева начинает с графа без рёбер и добавляет их; при этом

на каждом шаге выбирается ребро наименьшего веса, которое не создаёт цикла.

Этот алгоритм жадный (можно было бы опасаться, что добавление какого-то лёгкого ребра потом вынудит нас добавить очень тяжёлое, но мы про это не думаем).

DRAFTКорректность алгоритма Крускала следует из свойства разреза, которое носит общий характер и используется также в других алгоритмах построения минимальных покрывающих деревьев.

На рисунке 5.1 мы упорядочиваем рёбра по возрастанию (неубыванию)

весов:

B–C, C–D, B–D, C–F, D–F, E–F, A–D, A–B, C–E, A–C.

Добавляем их одно за другим, если не возникает цикла: первые два годятся, третье ребро B–D при добавлении создаёт цикл, так что мы его пропускаем, и т. д. Окончательный результат –– дерево с минимально возможной сто-

имостью 14.

Рис. 5.1. Минимальное покрывающее дерево, построенное алгоритмом Крускала.

5.1.2. Свойство разреза

Предположим, что мы строим минимальное покрывающее дерево, уже выбрали какие-то рёбра и пока на правильном пути (эти рёбра можно дополнить до минимального покрывающего дерева). Какое ребро нужно добавить дальше? Следующее свойство даёт больш´ую свободу выбора.

Разрез (cut) –– это произвольное разбиение вершин на две части S и V S. Здесь и далее под V S понимается разность множеств V и S (элементы V , не входящие в S), которая также часто обозначается как V n S.

Свойство разреза. Пусть рёбра множества X входят в минимальное покрывающее дерево для графа G = (V, E). Пусть S V –– множество вершин, и ни одно ребро из X не соединяет вершину из S с вершиной из V S. Наконец, пусть e –– ребро с наименьшим весом, соединяющее S и V S. Тогда X [ feg является частью некоторого минимального покрывающего дерева.

Данное свойство утверждает, что если стороны разреза пока не соединены рёбрами, то к X можно добавить минимальное из соединяющих их рёбер, причём X останется частью некоторого минимального покрывающего дерева, если это было так до того.

Почему? Пусть T –– минимальное покрывающее дерево, содержащее все рёбра из X . Оно может не содержать e (если содержит, всё доказано). В этом случае концы ребра e соединены некоторым путём в T , который вместе с e

e

e0

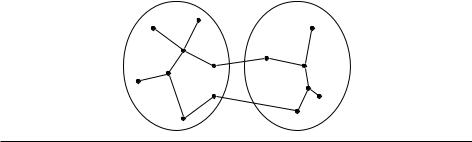
образует цикл. Поскольку e пересекает разрез, то в этом цикле есть и другое ребро e0, пересекающее разрез (перейдя на другую сторону разреза, мы должны вернуться обратно). Это ребро лежит в дереве T . Замена e0 на e в этом дереве даёт связный граф с тем же числом рёбер, то есть тоже дерево. Получили новое покрывающее дерево, которое не хуже старого (вес e0 не меньше веса e, который был минимальным по предположению среди всех рёбер, пересекающих разрез) и содержит X [ feg, что и требовалось. (Заметим, что выкинутое ребро e0 пересекало разрез и потому не могло быть в X .)

Рис. 5.3 иллюстрирует свойство разреза. Где там ребро e0?

5.1.3. Алгоритм Крускала

Теперь легко показать, что алгоритм Крускала корректен. В каждый момент выбранные рёбра образуют лес (набор деревьев). По индукции покажем, что это лес является частью некоторого минимального покрывающего дерева. Следующее добавляемое ребро e соединяет две компоненты, обозначим их через T1 и T2. Так как e –– ребро наименьшего веса между разными компонентами, оно будет ребром наименьшего веса между T1 и V T1. Остаётся воспользоваться свойством разреза.

Опишем некоторые детали реализации. На каждом шаге алгоритм добавляет новое ребро к уже имеющимся. При этом надо уметь проверять для каждого возможного ребра fu, vg, лежат ли u и v в разных компонентах. А после добавления соответствующие компоненты необходимо объединить. Какая структура данных поддерживает такие операции?