Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

2.6. Быстрое преобразование Фурье

Используя метод «разделяй и властвуй», мы научились быстро умножать числа и матрицы. Научимся теперь быстро умножать многочлены (полиномы). Произведение двух многочленов степени d есть многочлен степени 2d, например,

(1 + 2x + 3x2) (2 + x + 4x2) = 2 + 5x + 12x2 + 11x3 + 12x4.

DRAFTбыстрое преобразование Фурье –– произвёл революцию в цифровой обработке сигналов (да и вообще сделал её возможной). Этот важный для практического применения алгоритм (его текст приведён в разделе 2.6.4) мы рассмотрим подробно.

2.6.1. Альтернативное представление многочленов

Быстрый алгоритм умножения использует такое свойство многочленов:

Факт. Многочлен степени d однозначно задаётся значениями в любых d + 1 различных точках.

В частности, как известно, любые две различные точки задают прямую (график многочлена первой степени).

Выберем произвольные d + 1 точек x0, ‌, xd . Многочлен степени не выше d имеет вид A(x) = a0 + a1 x + ‌ + ad xd , и его можно задать одним из двух способов:

ff коэффициентами a0, ‌, ad , ff значениями A(x0), ‌, A(xd ).

Второе представление более удобно для умножения: зная значения сомножителей в каждой из точек, легко вычислить значение произведения (число умножений равно числу точек, то есть пропорционально степени многочлена). Итак, если многочлены задаются своими значениями, то их умножение занимает линейное время.

Для чего нужно умножать многочлены?

Прежде всего, самые быстрые из известных алгоритмы умножения чисел основаны на умножении многочленов (задачи умножения чисел и многочленов родственны: достаточно заменить x на основание системы

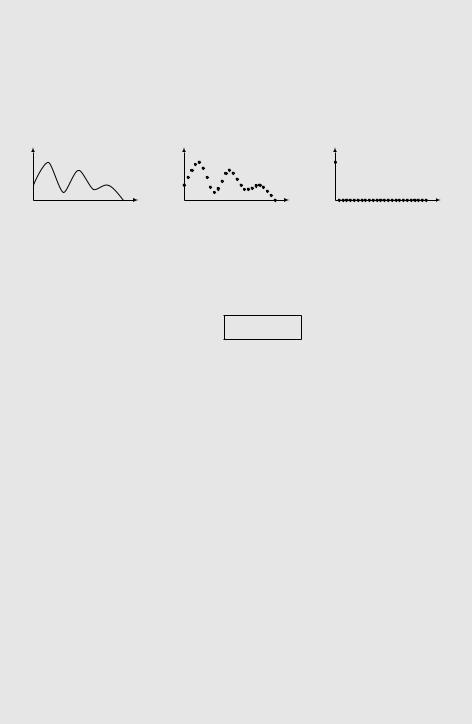
счисления и следить за переносами). Но, пожалуй, наиболее важное применение умножения многочленов –– цифровая обработка сигналов (signal processing). Сигналом (a) называется произвольная функция времени или координаты. Например, человеческий голос будет звуковым сигналом, отражающим колебания воздуха у рта говорящего. Картину ночного неба тоже можно считать сигналом (только двумерным), измеряя яркость как функцию координат.

Обрабатывая сигнал, мы дискретизируем его, беря значения через определённые промежутки времени (b). Посмотрим, как такой сигнал проходит через некоторую преобразующую его систему. Выходной сигнал такой системы называют откликом:

входной сигнал ! СИСТЕМА ! отклик

Важный класс составляют системы, которые обладают свойством линейности (отклик на сумму сигналов равен сумме откликов на каждый из них по отдельности) и инвариантности по времени (сдвинутый на время t сигнал приводит к сдвинутому на то же время отклику). Любая система, обладающая этими свойствами, полностью характеризуется реакцией на самое простое возможное воздействие –– единичный импульс (t) (unit impulse), равный единице в момент времени t = 0 и нулю в остальное время (c). Чтобы убедиться в этом, рассмотрим задержанный импульс (t i), равный единице в момент времени i. Любой сигнал a(t) можно представить как линейную комбинацию задержанных импульсов:

T 1

X

a(t) = a(i) (t i)

i=0

(если сигнал состоит из T отсчётов). По свойству линейности отклик на сигнал a(t) определяется откликом на различные (t i). А по свойству инвариантности эти отклики получаются сдвигом импульсной характеристики b(t) (impulse response) –– реакции системы на импульс (t).

Другими словами, отклик системы задаётся формулой

k

X

i=0

а это в точности формула умножения многочленов!

Многочлены, однако, обычно даны нам в виде списка коэффициентов, и произведение необходимо вычислить в таком же виде. Поэтому умножение будет в три этапа: сначала мы перейдём от коэффициентов к значениям в точках, то есть вычислим значения многочлена в этих точках. После этого найдём значения произведения в точках и, наконец, произведём интерполяцию (interpolation), то есть восстановим коэффициенты произведения по его значениям.

DRAFT2.6.2. Вычисление методом «разделяй и властвуй»

Соответствующий алгоритм приведён на рис. 2.5. Ясно, что алгоритм корректен, но насколько он эффективен? Умножение значений требует линейного времени.1 Но сколько времени нужно для вычисления значений (и интерполяции, о которой мы пока почти ничего не знаем)? Значение многочлена степени d ¶ n в точке можно вычислить за O(d) операций (упражнение 2.29), поэтому значения многочлена степени n в n точках можно вычислить за (n2) операций. Быстрое преобразование Фурье решает эту задачу за время O(n log n) для специально выбранных точек x0, x1, ‌, xn 1; ускорение происходит за счёт того, что одни и те же вычисления оказываются полезны

для разных точек.

Рис. 2.5. Алгоритм умножения многочленов.

{Вход: коэффициенты многочленов A(x) и B(x) степени не выше d.} {Выход: коэффициенты многочлена C = A B.}

выбор

выбрать точки x0, x1, ‌, xn 1 в количестве n ¾ 2d + 1

вычисление

вычислить A(x0), A(x1), ‌, A(xn 1) и B(x0), B(x1), ‌, B(xn 1)

умножение

вычислить C(xk) = A(xk)B(xk) для всех k = 0, 1, ‌, n 1

интерполяция

восстановить C(x) = c0 + c1 x + ‌ + c2d x2d

Допустим, что для вычисления значений многочлена A(x) степени не выше n 1 мы выбрали n точек, разбитых на пары отличающихся знаком:

x0, x1, ‌, xn=2 1.

1Мы считаем, что коэффициенты многочленов являются вещественными числами и что их размер позволяет производить с ними арифметические операции (сложение и умножение) за один шаг. Оценки, которые мы получим, легко обобщаются и на случай больших коэффициентов.

Ясно, что вычисления значений A(xi ) и A( xi ) имеют много общего, поскольку чётные степени xi и xi совпадают.

Чтобы воспользоваться этим, выделим в A(x) мономы чётных и нечётных степеней, скажем,

3 + 4x + 6x2 + 2x3 + x4 + 10x5 = (3 + 6x2 + x4) + x(4 + 2x2 + 10x4).

Выражения в скобках являются многочленами от x2. В общем случае, много-

Этим способом задача размера n сводится к двум задачам размера n=2, после чего за линейное время можно найти ответ. Если бы мы могли использовать эту идею рекурсивно, то получили бы соотношение

T (n) = 2T 2n + O(n),

из которого бы следовала желаемая оценка O(n log n).

Проблема же здесь в том, что выбранные нами числа разбиты на пары лишь на первом шаге. Чтобы продолжить рекурсию, нам нужно, чтобы числа x02, x12, ‌, xn2=2 1 тоже были разбиты на пары отличающихся знаком, но это

невозможно, поскольку квадрат числа не может быть отрицательным.

Зато так может быть для комплексных чисел, в отличие от вещественных. Так почему бы не использовать комплексные числа? Но какие именно? Чтобы понять это, давайте посмотрим, чем должна закончиться рекурсия. На

последнем шаге у нас останется одна точка; пусть это будет 1. Тогда на предыдущем шаге были корни из 1, то есть 1:

.

На уровне выше тогда будут опять p1 = 1, но теперь ещё и p 1 = i, где i –– комплексный корень из 1. Поднимаясь выше, мы должны прийти к изначальным n точкам. Наверное, вы уже догадались, какими будут эти точки: это комплексные корни n-й степени из единицы (complex nth roots of unity), то есть n решений уравнения zn = 1. (Здесь n –– степень двойки.)

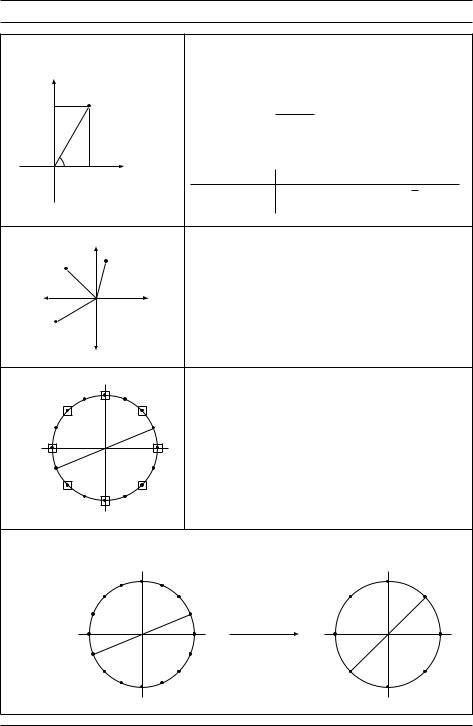
На рис. 2.6 приведены основные факты о комплексных числах. В третьей сверху части рисунка показаны корни n-й степени из единицы, то есть числа 1, !, !2, ‌, !n 1, где ! = e2 i=n.

Для чётного n верны следующие утверждения:

1. Корни n-й степени из единицы разбиваются на пары так, что числа в парах отличаются только знаком: !n=2+j = !j .

2. Квадраты корней n-й степени –– это корни степени n=2.

Таким образом, начав с корней степени n, где n есть степень двойки, мы последовательно будем получать подзадачи для корней степени n=2k для k = 0, 1, 2, ‌ Как мы говорили, такие корни разбиваются на пары, что позволяет нам использовать метод «разделяй и властвуй». Соответствующий алгоритм называется быстрым преобразованием Фурье (fast Fourier transform, FFT, см. рис. 2.7).

2.6.3. Интерполяция

Вернёмся к нашей схеме умножения многочленов (рис. 2.5).

Если точки xi являются корнями (1, w, w2, ‌, wn 1) n-й степени из единицы, то при помощи быстрого преобразования Фурье можно перейти от коэф-

вернуть A(!0), ‌, A(!n 1)

фициентов многочлена к его значениям в этих точках за время O(n log n): hзначенияi = FFT(hкоэффициентыi, !).

Но как перейти обратно (выполнить интерполяцию)? Поразительным образом оказывается, что

hкоэффициентыi = 1n FFT(hзначенияi, ! 1).

Обратный переход, таким образом, осуществляется с помощью всё того же быстрого преобразования Фурье, но с ! 1 вместо !. На первый взгляд это кажется чудесным совпадением. Мы убедимся в верности этого факта, переформулировав операции с многочленами в терминах линейной алгебры. А пока отметим, что все шаги нашего алгоритма умножения многочленов за время O(n log n) (рис. 2.5) теперь полностью определены.

Формулировка в терминах матриц

Интересующее нас утверждение (интерполяция –– это тоже преобразование Фурье) в конечном счёте сводится к несложному вычислению (по формуле для суммы геометрической прогрессии). Но полезно понимать более общий контекст в терминах линейной алгебры.

Мы имеем дело с двумя представлениями многочленов степени не выше n 1: в виде вектора коэффициентов и в виде вектора значений. Переход от коэффициентов к значениям –– линейное преобразование, и матрицу этого преобразования легко написать:

Эта матрица называется матрицей Вандермонда (Vandermonde matrix).

Как мы уже говорили, коэффициенты многочлена степени не выше n 1 однозначно восстанавливаются по его значениям в n точках. В терминах линейной алгебры это соответствует такому свойству матрицы Вандермонда M:

Если x0, ‌, xn 1 попарно различны, то M обратима.

Задача интерполяции состоит в нахождении обратного преобразования, которое, как учит линейная алгебра, сводится к умножению на обратную мат-

рицу:

Вычисление значений есть умножение на M, а интерполяция –– умножение на M 1.

Задача интерполяции состоит в нахождении обратной матрицы, и нам

нужно показать, что в интересующем нас случае матрицы Вандермонда M(!) для точек xi = !i , где !n = 1, имеет место следующее равенство.

Формула обращения.

Mn(!) 1 = 1n Mn(! 1).

Заметим, что ! 1 тоже будет корнем из единицы (сопряжённым к !).

Матрица интерполяции

Как мы видели, преобразование Фурье умножает произвольный вектор размера n, содержащий коэффициенты многочлена, на (n n)-матрицу

где ! –– корень степени n из 1 (в качестве n мы берём степень двойки, но сейчас это не важно). Другими словами, (j, k)-й элемент [Mn(!)]j,k равен !jk (при нумерации строк и столбцов с нуля).

Нам осталось доказать такой факт:

Лемма. Mn(!)Mn(! 1) = nI, где I –– единичная матрица.

Доказательство. В самом деле, (j, k)-й элемент такого произведения по определению равен

Это сумма геометрической прогрессии со знаменателем !j k. Если знаменатель равен 1, то есть j = k, то все члены суммы равны и вся сумма равна n. В противном случае по формуле суммы геометрической прогрессии получаем (1 !n(j k))=(1 !(j k)), что равно нулю, поскольку !n = 1.

В терминах линейной алгебры можно сказать немного иначе. Матрица Mn(! 1) является эрмитово сопряжённой к матрице Mn(!), то есть получается транспонированием (что в данном случае не меняет матрицы) и сопряжением всех её элементов по формуле (a + bi) = a bi; в полярных координатах сопряжение комплексного числа соответствует изменению знака угла, то есть переходу от z = rei к z = re i . Для комплексного числа z единичной длины (в частности, для корней из единицы) z = z 1. Наше равенство приобретает вид M M = nI, что означает, что столбцы матрицы M ортогональны относительно скалярного произведения (inner product)

u v = u0 v0 + ‌ + un 1 vn 1

и имеют длину pn. Можно сказать ещё, что в пространстве многочленов степени не выше n 1 у нас есть два базиса: один –– обычный, состоящий из одночленов, и другой –– базис Фурье, в котором координаты многочлена –– это его значения в корнях из единицы. Матрица Mn(!) преобразует координаты из первого базиса во второй, и при этом она унитарна (с точностью до коэффициента), то есть эти два базиса задают одно и то же скалярное произведение в пространстве многочленов (опять же с точностью до коэффициента).

В базисе Фурье умножать многочлены легко, поэтому для умножения многочленов, заданных наборами коэффициентов, мы переходим к базису Фурье, после чего вычисляем произведение и результат переводим обратно в стандартный базис (интерполяция). Быстрое преобразование Фурье позволяет легко переходить от одного базиса к другому (в обе стороны).

2.6.4. Ещё о быстром преобразовании Фурье

Итак, мы описали все шаги нашей схемы умножения многочленов. Рассмотрим теперь детали реализации самой важной части –– быстрого преобразования Фурье.

Алгоритм быстрого преобразования Фурье

Входом БПФ является вектор a = (a0, ‌, an 1) и комплексное число !; оно является первообразным корнем степени n из единицы, то есть его степени 1, !, !2, ‌, !n 1 различны и среди них есть все корни n-й степени из едини-

Возможность использования метода «разделяй и властвуй» становится яснее, если переставить координаты на входе (и соответствующие столбцы мат-

рицы), разделив их на чётные и нечётные:

Видно, что в левом верхнем и в левом нижнем углах теперь стоит матри-

Мы свели вычисление произведения матрицы Mn(!) на вектор (a0, ‌, an 1), то есть задачу размера n, к двум задачам размера n=2 –– вычислению произведения Mn=2(!2) на (a0, a2, ‌, an 2) и на (a1, a3, ‌, an 1). Получился (рис. 2.8) тот же самый рекурсивный алгоритм быстрого преобразования Фурье, кото-