Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

3.25. Дан ориентированный граф, каждой вершине u 2 V которого приписана цена (price) pu, представляющая собой целое положительное число. Определим массив cost следующим образом:

cost[u] = минимальная цена вершин, достижимых из u (включая u).

Например, значения массива cost для вершин A, B, C, D, E, F графа на рисунке равны 2, 1, 4, 1, 4, 5. (Цены pu указаны около вершин.)

Необходимо заполнить массив cost для всех вершин графа.

(a) Постройте линейный алгоритм для ориентированных ациклических графов. (Подсказка: обрабатывайте вершины в определённом порядке.)

(b) Обобщите алгоритм так, чтобы он (по-прежнему за линейное время) решал задачу для произвольных ориентированных графов. (Подсказка: вспомните о метаграфе из компонент сильной связности.)

3.26. Эйлеровым циклом (Eulerian tour) неориентированного графа называется замкнутый путь, проходящий по всем рёбрам графа ровно по одному разу. В 1736 году Леонард Эйлер решил знаменитую задачу о кёнигсбергских мостах, положившую начало теории графов. В Кёнигсберге (в настоящее время Калининград, Россия) два острова и два берега реки были связаны семью мостами, и возник вопрос: можно ли обойти все эти семь мостов и вернуться в исходную точку, пройдя по каждому из мостов ровно один раз?

Соответствующий граф приведён ниже. Отметим, что в нём есть кратные рёбра (несколько рёбер между парой вершин; мы такого не допускали).

(a) Докажите, что в неориентированном графе есть эйлеров цикл тогда и только тогда, когда он связен и степени всех его вершин чётны.

мула выполнима. (Подсказка: покажите, что следующий алгоритм строит выполняющий набор для формулы. Выбираем в метаграфе GI компоненту-сток и присваиваем значение true всем литералам из неё и значение false отрицаниям всех таких литералов, после чего выкидываем все литералы, у которых уже есть значения.)

(f) Наконец, используя все приведённые выше идеи, покажите, что задача 2-выполнимости решается за линейное время.

3.29. Бинарным отношением (binary relation) на конечном множестве на-

DRAFT S

зывается множество R упорядоченных пар (x, y) 2 S S. Если, например, S является множеством людей, то пара (x, y) 2 R может означать, что x знает y. Отношением эквивалентности (equivalence relation) называется бинарное отношение, удовлетворяющее трём свойствам:

ff рефлексивность (reflexivity): (x, x) 2 R для всех x 2 S;

ff симметричность (symmetry): если (x, y) 2 R, то и (y, x) 2 R;

ff транзитивность (transitivity): если (x, y) 2 R и (y, z) 2 R, то и (x, z) 2 R.

Например, отношение «у x и y дни рождения в один день» является отношением эквивалентности, а «x является отцом y» –– нет (не выполняется ни одно из трёх условий).

Покажите, что отношение эквивалентности разбивает множество S на непересекающиеся множества S1, S2, ‌, Sk (то есть S = S1 [ S2 [ ‌ [ Sk и Si \ Sj = ? для всех i 6= j), при этом

ff любые два элемента одного подмножества эквивалентны: (x, y) 2 R для любых x, y из любого Si ;

ff элементы же разных подмножеств не эквивалентны: (x, y) 2= R для любых x 2 Si и y 2 Sj при i 6= j.

(Подсказка: представьте отношение эквивалентности как неориентированный граф.)

3.30.На с. 93 мы ввели отношение «x связан с y» на множестве вершин ориентированного графа. Покажите, что оно является отношением эквивалентности (см. предыдущее упражнение) и разбивает граф на компоненты сильной связности.

3.31.Компоненты двусвязности. Рассмотрим неориентированный граф G = = (V, E). Будем говорить, что e e0 для двух рёбер e, e0 2 E, если e = e0 или же существует простой цикл, содержащий одновременно e и e0.

(a) Покажите, что отношение является отношением эквивалентности (см. упражнение 3.29).

Классы эквивалентности, на которые данное отношение разбивает множество рёбер, называются компонентами двусвязности (biconnected components) графа G. Мостом (bridge) называется ребро, в компоненту двусвязности которого входит только оно само. Точкой сочленения (separating vertex) называется вершина, удаление которой делает граф несвязным.

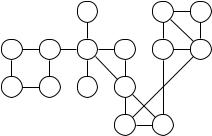
104 Глава 3. Декомпозиция графов

(b) Разбейте рёбра приведённого ниже графа на компоненты двусвязно-

Таким образом, мы получаем разбиение рёбер на классы эквивалентности (двусвязные компоненты); одновременно мы почти что разбиваем вершины графа на классы. А именно:

(c)Для каждой компоненты двусвязности рассмотрим множество концов входящих в эту компоненту рёбер. Покажите, что эти множества для двух различных компонент двусвязности либо не пересекаются вовсе, либо пересекаются по точке сочленения.

(d)Стянем теперь каждую компоненту двусвязности в отдельную «метавершину», сохранив также все точки сочленения (таким образом, метавер- шина-компонента будет соединена со всеми её точками сочленения). Покажите, что полученный граф является деревом.

Компоненты двусвязности, мосты и точки сочленения графа можно найти за линейное время при помощи поиска в глубину.

(e)Покажите, что корень дерева поиска в глубину является точкой сочленения тогда и только тогда, когда у него более одного ребёнка.

(f)Покажите, что некорневая вершина v дерева поиска в глубину является точкой сочленения тогда и только тогда, когда у неё есть ребёнок v0, для которого ни v0, ни его потомки не имеют обратного ребра, ведущего в предка вершины v (само v не считается своим предком).

(g)Для каждой вершины u положим low(u) равным минимальному значению среди pre(u) и всех значений pre(w) для всех обратных рёбер (v, w), у которых v –– потомок u. Покажите, что массив значений low можно заполнить за линейное время.

(h)Покажите, как найти компоненты двусвязности, мосты и точки сочленения графа за линейное время. (Подсказка: используйте значения массива low для нахождения точек сочленения. Запустите поиск в глубину с дополни-DRAFT

тельным стеком рёбер, чтобы по одной удалять компоненты двусвязности.)

Глава 4

Пути в графах

4.1. Расстояния в графе

Поиск в глубину не только быстро находит все вершины, достижимые из начальной, но и строит дерево, содержащее пути к ним (рис. 4.1). Однако эти пути не обязательно будут кратчайшими: например, от S до C можно добраться по одному ребру, в то время как поиск в глубину находит путь из трёх. А как искать кратчайшие, мы изучим в этой главе.

Расстоянием (distance) между двумя вершинами неориентированного графа будем называть длину кратчайшего пути между ними, измеренную в рёбрах. У этого понятия есть простой физический смысл. Представим себе граф из шариков (вершин), соединённых нитками одинаковой длины (рёбрами). Потянем граф вверх за вершину s; за ней потянутся все вершины, достижимые из s. Чтобы найти расстояния от них до s, мы можем теперь просто измерить, насколько они ниже s.

Например, на рис. 4.2 расстояние между вершинами S и B равно 2, и есть два кратчайших пути между ними. Когда граф подвешен за S, все рёбра этих

Рис. 4.1. (a) Простой граф и (b) его дерево поиска в глубину.

Рис. 4.2. Физическая модель графа.

двух путей натягиваются. А ребро (D, E) провисает, поскольку не входит ни в один из кратчайших путей из вершины S.

4.2. Поиск в ширину

Вершины графа рис. 4.2, подвешенного за S, разбиваются на слои: сама S, вершины на расстоянии 1 от S, вершины на расстоянии 2 и так далее. Можно находить расстояния от S до всех вершин, переходя от уровня к уровню.

Когда вершины уровней 0, 1, 2, ‌, d определены, легко найти вершины уров- DRAFTня d + 1: это просто ещё не просмотренные вершины, смежные с вершина-

ми уровня d. Эти рассуждения наталкивают нас на алгоритм, работающий в каждый момент с двумя уровнями: некоторым уровнем d, который уже полностью известен, и уровнем d + 1, который находится просмотром соседей вершин уровня d.

Поиск в ширину (breadth-first search, BFS) непосредственно реализует эту простую идею (рис. 4.3). Изначально очередь Q содержит только вершину S, то есть вершину на расстоянии 0. Для каждого последующего расстояния d = 1, 2, 3, ‌ найдётся момент времени, в который Q содержит все вершины на расстоянии d и только их. Когда все эти вершины будут обработаны (извлечены из очереди), их непросмотренные соседи окажутся добавленными в конец очереди, то есть мы перейдём к следующему значению d.

Запустим этот алгоритм для вершины S в графе рис. 4.1. Считаем, что соседи каждой вершины обрабатываются в алфавитном порядке. На рис. 4.4 слева показан порядок обхода вершин, а справа изображено дерево поиска в ширину. Оно содержит только рёбра, при переходе по которым обнаруживались новые вершины. В отличие от дерева поиска в глубину все пути данного дерева с началом в S являются кратчайшими. Поэтому оно называется деревом кратчайших путей (shortest-path tree).

Рис. 4.3. Поиск в ширину.

процедура BFS(G, s)

fВход: граф G(V, E), вершина s 2 V .g

fВыход: для всех вершин u, достижимых из s, dist[u] будет равно расстоянию от s до u.g

для всех вершин u 2 V : dist[u] 1

dist[s] 0

Q fsg fочередь из одного элементаg

пока Q не пусто:

u Eject(Q)

для всех рёбер (u, v) 2 E:

если dist[v] = 1:

Inject(Q, v)

dist[v] dist[u] + 1

Рис. 4.4. Результат поиска в ширину для графа рис. 4.1.

Этот алгоритм можно применять и к ориентированным графам. В них тоже можно определить расстояние от вершины S до вершины T как минимальное число рёбер, которое надо пройти (в их направлении), чтобы из S попасть в T . Расстояние при этом уже не будет симметрично, но понятие кратчайшего пути имеет смысл, и наш алгоритм по-прежнему годится.

Корректность и время работы

Убедимся в корректности алгоритма. Мы утверждаем, что

для всех d = 0, 1, 2, ‌ найдётся момент времени, когда: 1) для всех вершин на расстоянии не более d это расстояние уже помещено в массив dist; 2) для всех оставшихся вершин значения в dist равны 1; 3) очередь содержит в точности вершины на расстоянии d.

Данное утверждение легко доказывается по индукции (проверьте).

Как и в случае поиска в глубину, время работы поиска в ширину линейно, то есть равно O(jV j + jEj). Действительно, каждая вершина помещается в очередь ровно один раз –– при её обнаружении. Поэтому общее количество операций с очередью есть 2jV j. Вся оставшаяся работа производится во внутреннем цикле алгоритма. На это требуется время O(jEj), поскольку каждое ребро в данном цикле просматривается один раз (для ориентированных графов) или два раза (для неориентированных).

Теперь, когда мы знаем и поиск в глубину, и поиск в ширину, интересно сравнить их способы обхода графа. Поиск в глубину стремится вперёд, и возвращается назад, чтобы пойти вбок, только если впереди уже нет новых вершин. Поэтому он может долго добираться до вершины, которая находится совсем близко (рис. 4.1). Поиск в ширину обходит вершины в порядке увеличения расстояний до них от начальной вершины, как фронт волны на воде.

Если в алгоритме поиска в ширину заменить очередь на стек (вынимается первым тот элемент, который положен последним), то он превратится в поиск в глубину (в нерекурсивном варианте).

При поиске в ширину нас интересуют расстояния от s, поэтому мы не перезапускаем поиск в других связных компонентах (недоступные вершины просто игнорируются).

Будильники

Очевидный недостаток такого решения состоит в том, что при длинных рёбрах нужно много вспомогательных вершин, и алгоритм будет тратить много времени, двигаясь от одного столба до другого.

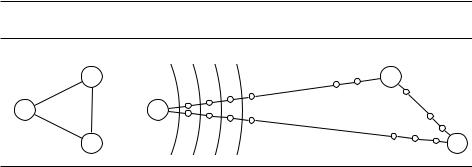
Для примера рассмотрим граф G и граф G0 с добавленными вершинами, показанные на рис. 4.7. Запустим из S поиск в ширину (со скоростью ребро за минуту). Тогда первые 99 минут он будет двигаться вдоль S–A и S–B от

столба к столбу. На это и смотреть скучно, так что мы лучше поспим до того момента, когда произойдёт что-то интересное (мы дойдём до настоящей вершины). Поставим два будильника: один на время 100 для вершины A, второй –– на 200 для B. Первый сработает раньше: поиск дойдёт сначала до вершины A. Из A начнётся новое движение, которое дойдёт до B в момент 150 (раньше, чем движение из S).

DRAFTОпишем ситуацию в общем виде: поиск в ширину продвигается по рёбрам графа G, и для каждой вершины установлен будильник на ожидаемое время прибытия уже запущенного движения. (Реально поиск может прийти туда и раньше, пройдя через другую вершину, как это было в примере.) Главное: пока не сработает хотя бы один будильник, ничего интересного не будет (движение будет продолжаться по рёбрам). Звонок будильника означает, что поиск в ширину добрался до некоторой вершины исходного графа u 2 V . В этот момент начинаются движения по рёбрам, исходящим из u, и это надо учесть в их концевых вершинах и перезавести будильники на концах этих рёбер (если новое время прибытия раньше прежнего). Вот схема алгоритма:

Рис. 4.7. Поиск в ширину на новом графе. Пунктирные линии показывают начальные «фронты волн».

ff Завести будильник для s на время 0.

ff Пока есть заведённые, но не сработавшие будильники:

–– Взять самый ранний из них (пусть он в вершине u на момент T ). –– Констатировать, что расстояние от s до u равно T .

–– Для каждой вершины v, смежной с u в G:

если для вершины v будильник ещё не заведён, завести его на время

T + l(u, v);

если будильник заведён на время, большее чем T + l(u, v), то переставить его на это меньшее время (а иначе оставить как было).

110 Глава 4. Пути в графах

Алгоритм Дейкстры

Алгоритм с будильниками находит кратчайшие пути в графах с положительными целыми весами. Он практически готов к использованию, осталось только как-нибудь реализовать механизм будильников. Подходящая для этих целей структура данных называется очередью с приоритетами; обычно её реализуют с помощью кучи. Очередь с приоритетами хранит множество элементов (в нашем случае –– вершин графа) и соответствующих им числовых значений –– ключей (ожидаемое время, в которое прозвонит будильник) DRAFTи выполняет следующие операции:

Insert: добавить новый элемент (с указанным ключом) в очередь.

DecreaseKey: уменьшить ключ, соответствующий заданному элементу очереди, до заданного значения.

DeleteMin: выдать элемент с минимальным ключом, удалив его из очереди.

MakeQueue: построить очередь из заданных элементов с ключами (выделяется в особую операцию, поскольку иногда это быстрее, чем добавлять все элементы по очереди).

С помощью первых двух операций мы будем ставить и переставлять будильники, а с помощью третьей –– узнавать, какой из будильников прозвонит следующим. Всё вместе даёт алгоритм Дейкстры (D kstra) поиска кратчайших путей (рисунок 4.8).

Рис. 4.8. Алгоритм Дейкстры для нахождения кратчайших путей.

процедура Dijkstra(G, l, s)

{Вход: граф G(V, E) (ориентированный или нет) с неотрицательными длинами рёбер fle : e 2 Eg; вершина s 2 V .}

{Выход: для всех вершин u, достижимых из s,

dist[u] будет равно расстоянию от s до u (и 1 для недостижимых).}

для всех вершин u 2 V : dist[u] 1

prev[u] nil

dist[s] 0

H MakeQueue(V ) {в качестве ключей используются значения dist}

пока H не пусто:

u DeleteMin(H)

для всех рёбер (u, v) 2 E:

если dist[v] > dist[u] + l(u, v): dist[v] dist[u] + l(u, v)

prev[v] u

DecreaseKey(H, v, dist[v])