Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

(b)Найдите преобразование Фурье вектора (0, 1, 1, 1, 5, 2) по модулю 7, используя матричное представление, то есть умножьте данный вектор на M6(!) (для найденного ранее !). Все промежуточные вычисления производите по модулю 7.

(c)Запишите матрицу обратного преобразования Фурье. Покажите, что при умножении на эту матрицу получается исходный вектор. (Как и прежде, все вычисления должны производиться по модулю 7.)

(d)Перемножьте многочлены x2 + x + 1 и x3 + 2x 1 при помощи ПФ по модулю 7.

2.31.В разделе 1.2.3 мы познакомились с алгоритмом Евклида для вычисления наибольшего общего делителя (НОД) двух положительных целых чисел. Рассмотрим алгоритм вычисления НОД, основанный на методе «разделяй и властвуй».

(a)Докажите, что

(b)Постройте алгоритм, основанный на этом соотношении.

(c)Какой алгоритм будет быстрее для n-битовых чисел a и b при больших значениях n –– ваш или алгоритм Евклида? (Поскольку n велико, нельзя считать, что основные арифметические операции с числами производятся за один шаг.)

2.32.В данном упражнении мы построим алгоритм для геометрической задачи о паре ближайших точек.

DRAFTВход: список точек на плоскости

fp1 = (x1, y1), p2 = (x2, y2), ‌, pn = (xn, yn)g.

Выход: пара ближайших точек, то есть такая пара точек pi 6= pj , расстояние между которыми, вычисляемое как

Æ

jpi pj j = (xi x j )2 + (yi yj )2,

минимально (среди всех пар).

Будем для простоты считать, что n есть степень двойки и что все абсциссы и ординаты данных точек различны.

Ниже приведены основные идеи алгоритма.

ffНайдём такое x, что ровно для половины точек xi < x и ровно для половины точек xi > x. Разобьём точки на соответствующие два множества L и R.

ffРекурсивно найдём пары ближайших точек отдельно в L и R. Назовём найденные пары pL , qL 2 L и pR, qR 2 R, а расстояния между ними dL и dR соответственно. Пусть d = minfdL , dRg.

ffОстаётся проверить, есть ли в L точка, расстояние от которой до некоторой точки из R меньше d. Для этого удалим из рассмотрения все точки, для которых jxi xj> d, и упорядочим оставшиеся точки по значениям y.

ffТеперь пройдёмся по упорядоченному списку и для каждой точки вычислим расстояние от неё до семи следующих за ней точек. Пару таких точек с минимальным расстоянием назовём fpM , qM g.

ffОтветом считаем наилучшую из пар fpL , qL g, fpR, qRg, fpM , qM g.

(a)Покажите, что любой квадрат размера d d на плоскости содержит не более четырёх точек из L.

(b)Докажите корректность алгоритма. (Сложен лишь случай, когда одна из точек искомой пары попала в L, а другая –– в R.)

(c)Напишите псевдокод алгоритма и покажите, что время его работы удовлетворяет соотношению

(d)Как улучшить алгоритм, сократив время работы до O(n log n)?

2.33.Даны три (n n)-матрицы A, B, C. Мы хотим проверить равенство AB = C. Это можно сделать за время O(nlog2 7), воспользовавшись алгоритмом Штрассена. Но есть и более быстрый вероятностный алгоритм для такой проверки.

(a)Пусть v –– случайный n-мерный вектор, каждая компонента которого выбирается равновероятно и независимо из множества f0, 1g. Докажите, что для любой ненулевой (n n)-матрицы M вероятность того, что Mv = 0, не больше 1=2.

(b)Покажите, что P(ABv = Cv) ¶1=2 при AB 6= C. Как использовать это для вероятностной проверки равенства AB = C за время O(n2)?

2.34.Линейная 3-выполнимость. Задача 3-выполнимости описана в разделе 8.1: дан набор дизъюнктов с тремя переменными и надо узнать, могут ли они одновременно быть истинными для какого-то набора значенийDRAFT

True/False.

Пусть дополнительно известно, что формула в 3-КНФ с n переменными обладает таким свойством «локальности»: если переменные с номерами i и j входят в один дизъюнкт, то jj ij ¶ 10. Постройте линейный по времени алгоритм проверки выполнимости для таких формул.

Глава 3

Декомпозиция графов

3.1. Откуда берутся графы

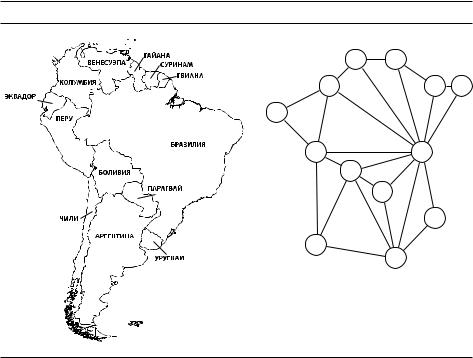
Многие важные задачи легко формулируются на языке графов. Пусть, например, мы хотим выбрать цвет для каждой страны на карте, при этом соседи должны иметь разные цвета (иначе не будет видна их общая граница). Какое минимальное число цветов для этого нужно? Видно, что карта (рис. 3.1(a)) содержит много лишнего: моря, реки и т. п. Достаточно построить граф (рис. 3.1(b)), изобразив каждую страну вершиной (в нашем примере 1 –– Бразилия, 11 –– Аргентина и т. д.) и соединив соседей ребром. Надо покрасить все вершины графа в минимальное число цветов, при этом концы каждого ребра должны быть разного цвета.

Рис. 3.1. Карта (a) и её граф (b).

Одна и та же математическая формулировка возникает в разных практических задачах. Пусть, например, мы хотим назначить даты экзаменов так,

84 Глава 3. Декомпозиция графов

чтобы никому не надо было сдавать два экзамена в один день, и при этом хотим занять поменьше дней. Заведём вершину для каждого экзамена и соединим две вершины ребром, если хотя бы один студент сдаёт оба экзамена. Раскрасив граф в минимальное число цветов, получим оптимальное расписание (экзамены одного цвета назначаются на один день).

В этой главе мы рассмотрим некоторые базовые алгоритмы, связанные с разбиением графа на части. Начнём с определений.

Граф задаётся множеством вершин V и множеством рёбер E, соединяю-

щих пары вершин. (Английская терминология: вершина называется vertex или node, а ребро –– edge.)

DRAFTМатрица смежности неориентированного графа, таким образом, симметрична. В таком представлении мы можем за время O(1) проверить, соединены ли данные вершины ребром (посмотрев на один элемент массива). В то же время хранение матрицы требует памяти O(n2), что во многих случаях неэкономно. Альтернативное представление –– список смежности (adjacency list). Требуемая при этом память пропорциональна размеру графа (сумме числа вершин и числа рёбер). Элементами списка смежности являются связные списки, по одному для каждой вершины графа. Для вершины u в таком списке хранятся вершины, в которые ведут рёбра из u, то есть вершины v, для которых (u, v) 2 E. Для ориентированного графа каждое ребро входит только в один из этих списков (для начальной вершины), а для неориентированного в два (для двух концов ребра). Список смежности, таким образом, тре-

В примере с картой V = f1, 2, 3, ‌, 13g, а рёбра из E соединяют страны, граничащие друг с другом (в частности, E содержит рёбра f1, 2g, f9, 11g и f7, 13g). Отношение «быть соседом» симметрично, так что ребро из x в y возникает одновременно с ребром из y в x. Поэтому мы записываем ребро, соединяющее x с y, как множество: fx, yg. Такие рёбра называются неориентированными (undirected), а соответствующий граф –– неориентированным гра-

фом (undirected graph).

Бывают и несимметричные отношения, и их изображают ориентированными рёбрами (directed edges). В ориентированном графе наличие ребра из x в y не гарантирует наличие ребра из y в x. Ориентированное ребро из x в y будем обозначать (x, y). Можно считать «всемирную паутину» (World Wide Web) ориентированным графом: из вершины u идёт ориентированное ребро в вершину v, если на странице u есть ссылка на страницу v. В этом графе миллиарды вершин и рёбер, так что алгоритмы, с ним работающие, должны быть быстрыми (к счастью, такие алгоритмы есть –– многое можно сделать

за линейное время).

3.1.1. Представление графа

Рассмотрим граф c n = jV j вершинами v1, ‌, vn. Его матрицей смежности (adjacency matrix) называется (n n)-матрица a, в которой

Матрица смежности или список смежности?

Что лучше? Ответ зависит от отношения между числом вершин jV j и числом рёбер jEj. Заметим, что jEj может быть довольно малым –– порядка jV j (если jEj сильно меньше jV j, то граф уже вырожденный –– в частности, содержит изолированные вершины). Или же довольно большим´ –– порядка jV j2 (если граф содержит все возможные рёбра). Графы с большим числом рёбер называют плотными (dense), с малым –– разреженными (sparse).

Выбирая алгоритм, полезно понимать, с какими графами ему в основном DRAFTпридётся иметь дело. Важно это и при хранении: если хранить веб-граф, в котором больше восьми миллиардов вершин, в виде матрицы смежности, то занимать она будет миллионы терабайтов, что сравнимо с общей ёмкостью всех жёстких дисков в мире. И дальше, скорее всего, будет только

хуже (матрица может расти быстрее, чем производство дисков).

А вот хранить граф Интернета в виде списка смежности вполне разумно, поскольку хранить нужно несколько десятков миллиардов гиперссылок, каждая из которых будет занимать в списке всего несколько байтов, и такого размера диск поместится в карман. Такая разница происходит из-за того, что граф Интернета очень разрежен: страница содержит в среднем пару десятков ссылок на другие страницы –– из нескольких миллиардов возможных.

бует памяти O(jV j + jEj). Проверка наличия ребра (u, v) теперь требует просмотра списка вершины u (что может быть больше O(1) шагов). Зато в этом представлении легко просмотреть всех соседей заданной вершины (что часто бывает необходимо). Список смежности для неориентированного графа симметричен (если u содержится в списке для v, то и v содержится в списке для u).

3.2. Поиск в глубину в неориентированных графах

3.2.1. Прохождение лабиринтов

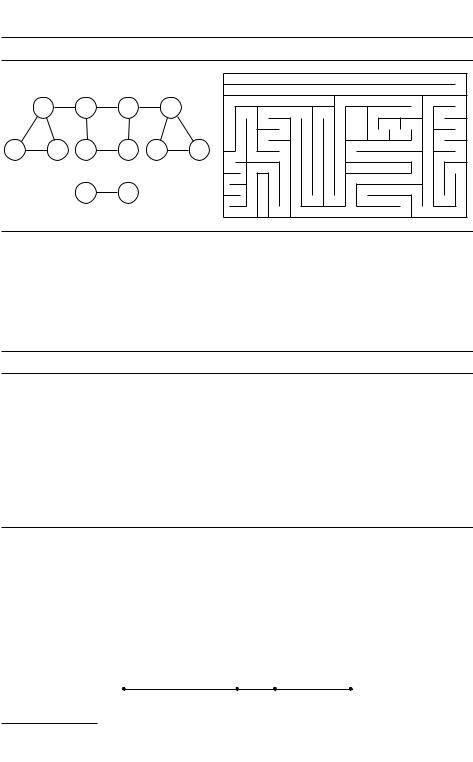
Поиск в глубину (depth-first search) отвечает на вопрос: какие части графа достижимы из заданной вершины? Это похоже на задачу обхода лабиринта: имея граф как список смежности, мы в каждой вершине «видим» её соседей –– как в лабиринте, где мы видим соседние помещения (рис. 3.2) и можем в них перейти. Но если мы будем это делать без продуманного плана, то можем ходить кругами, а в какую-то часть так и не попасть.

Обойти лабиринт можно с помощью клубка ниток (закрепив конец нитки в исходной точке и нося клубок с собой, мы всегда сможем вернуться) и мела (чтобы отмечать, где мы уже были, и не ходить туда ещё раз). Примерно так же работает алгоритм поиска в глубину. Чтобы хранить пометки, для каждой вершины будем хранить бит, показывающий, были мы в этой вершине или нет. Клубок ниток можно было бы заменить стеком (идя в новый коридор,

Выходит, что вершину z процедура посетила, а вершину w –– нет. Но так быть не может: ведь состоявшийся вызов Explore(z) должен был перебрать всех соседей z.

(Уточнение: начальный вызов процедуры Explore(v) предполагает, что visited[u] = false для всех вершин u; в противном случае она обработает лишь часть графа, где это было так.)

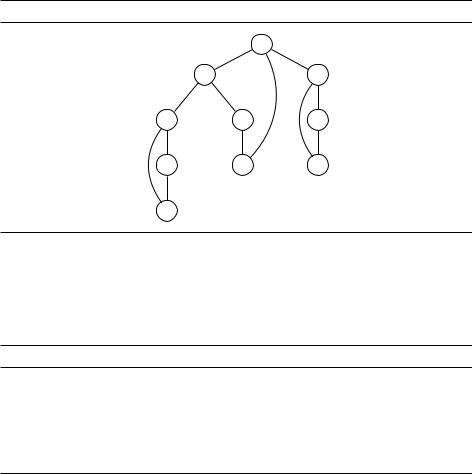
На рис. 3.4 показан вызов Explore для рассмотренного ранее графа и вершины A. Считаем, что соседи вершины перебираются в алфавитном поряд-

ке. Сплошными нарисованы рёбра, которые ведут в ранее не встречавшиеся DRAFTвершины. Например, когда процедура Explore находилась в вершине B, она

прошла по ребру B–E, и, поскольку в E она до этого не бывала, был произведён вызов Explore для E. Сплошные рёбра образуют дерево (связный граф без циклов) и поэтому называются древесными рёбрами (tree edges). Пунктирные же рёбра ведут в вершины, которые уже встречались. Такие рёбра называются обратными (back edges).

Рис. 3.4. Результат вызова Explore(A) для графа с рис. 3.2.

A

B D

E F G

I C H

J

3.2.2. Поиск в глубину

Процедура Explore обходит все вершины, достижимые из данной. Для обхода всего графа алгоритм поиска в глубину (рис. 3.5) последовательно вызывает Explore для всех вершин (пропуская уже посещённые).

Рис. 3.5. Поиск в глубину.

процедура DFS(G)

для всех вершин v 2 V : visited[v] false

для всех вершин v 2 V :

если visited[v] = false: Explore(v)

Сразу же отметим, что процедура Explore вызывается для каждой вершины ровно один раз благодаря массиву visited (пометки в лабиринте). Сколько времени уходит на обработку вершины? Она включает в себя:

1)O(1)-операции: пометка вершины, а также вызовы Previsit и Postvisit (мы не учитываем время внутри этих вызовов);

2)перебор соседей.

Общее время зависит от вершины, но можно оценить количество опе-

раций для всех вершин вместе. Общее количество операций на шаге 1 есть O(jV j). На шаге 2 (будем говорить о неориентированном графе) каждое реб-

DRAFT3.2.3. Связные неориентированные графы

ро fx, yg 2 E просматривается ровно два раза: при вызовах Explore(x) и

Explore(y). Общее время работы на шаге 2, таким образом, есть O(jEj). В целом время работы поиска в глубину есть O(jV j + jEj), то есть линейно. За меньшее время мы не успеем даже прочесть все вершины и рёбра!

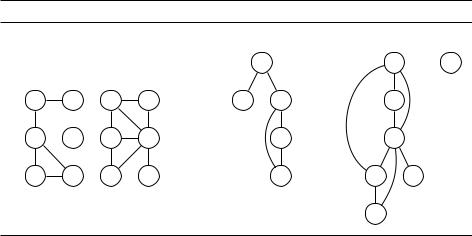
На рис. 3.6 показан поиск в глубину на графе с двенадцатью вершинами (не обращайте пока внимания на пары чисел). Опять считаем, что соседи перебираются в алфавитном порядке. Во внешнем цикле процедура Explore вызывается трижды –– для вершин A, C и F. Результатом является лес (forest)

из трёх деревьев с корнями в этих вершинах.

Рис. 3.6. (a) Граф на двенадцати вершинах. (b) Лес, построенный поиском в глубину.

Неориентированный граф называется связным (connected), если любые две его вершины соединены путём (по рёбрам). Граф на рис. 3.6 не связен: например, нет пути из A в K. Этот граф можно разбить на три непересекающихся связных подмножества:

fA, B, E, I, Jg, fC, D, G, H, K, Lg, fFg.

Они называются компонентами связности (connected components). Каждое из них образует связный подграф, а друг с другом они не соединены. Процеду-

ра Explore обходит как раз компоненту связности той вершины, для которой она была вызвана. При каждом вызове Explore во внешнем цикле алгоритма DFS обходится новая компонента связности. Таким образом, с помощью поиска в глубину легко проверить связность графа. Более того, можно для каждой вершины v найти номер её компоненты связности ccnum[v] (в порядке обнаружения). Для этого нужно завести переменную cc, изначально равную нулю, и увеличивать её на единицу каждый раз, когда Explore вызывается во внешнем цикле, а процедуру Previsit сделать такой:

DRAFTпроцедура Previsit(v) ccnum[v] cc

3.2.4. Время начала и конца обработки вершины

Как мы видим, поиск в глубину позволяет за линейное время определить, связен ли граф. И это далеко не всё –– сейчас мы рассмотрим приём, который лежит в основе многих других применений поиска в глубину. Будем записывать время начала обработки каждой вершины (вызов Previsit) и время конца обработки (Postvisit). Для нашего примера эти числа (для всех 24 таких событий) показаны на рис. 3.6. Например, в момент времени 5 началась обработка вершины I, а в момент времени 21 закончилась обработка вершины D.

Чтобы сохранить эту информацию при поиске в глубину, заведём счётчик clock, изначально равный 1, и напишем так:

процедура Previsit(v)

pre[v] clock clock clock + 1

процедура Postvisit(v)

post[v] clock clock clock + 1

Вот простое (но важное) свойство этих чисел:

Свойство. Для любых двух вершин u и v либо отрезки [pre(u), post(u)] и [pre(v), post(v)] не пересекаются, либо один содержится в другом.

В самом деле, [pre(u), post(u)] –– это промежуток времени, в течение которого вершина u была в стеке, и если вершина v была помещена в стек, когда там уже лежала вершина u, то v будет вынута раньше u.

Таким образом, рассмотренные отрезки отражают структуру дерева, построенного при поиске в глубину. Это особенно полезно для ориентированных графов, к которым мы и переходим.

3.3. Поиск в глубину в ориентированных графах

3.3.1. Типы рёбер

Рассмотренный нами алгоритм поиска в глубину может быть использован и для ориентированных графов (в процедуре Explore надо перебирать выходя-

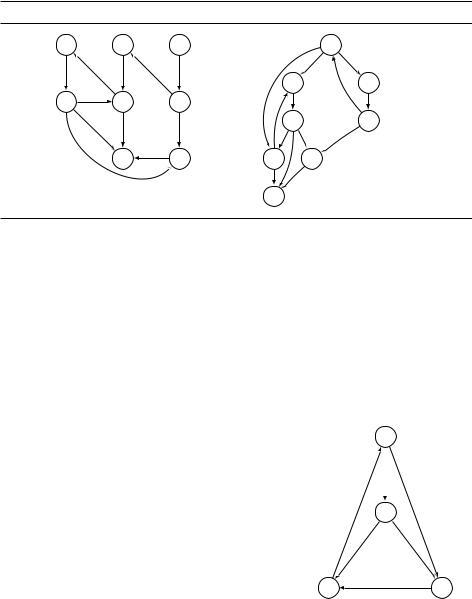
щие из вершины рёбра). На рис. 3.7 показан пример ориентированного графа и дерева, построенного поиском в глубину (напомним, что соседи перебираются в алфавитном порядке).

Рис. 3.7. Поиск в глубину для ориентированных графов.

B A C A 1, 16

Напомним общеизвестную терминологию, связанную с деревьями. Вершина A называется корнем дерева (tree root), все остальные вершины этого дерева являются её потомками (descendants). Вершины F, G, H являются потомками E, а E является их предком (ancestor). Наконец, C является родителем (parent) D, а D –– ребёнком (child) C. (В отличие от людей, у вершины дерева может быть только один родитель.)

При поиске в глубину в неориентированных графах мы различали древесные рёбра дерева и обратные (все остальные). Для ориентированных графов

На рис. 3.7 можно обнаружить два прямых, два обратных и два перекрёстных ребра (найдите их).