
Дасгупты, Пападимитриу, Вазирани «Алгоритмы»
.pdf
6.3. Расстояние редактирования |
161 |
В первом случае стоимость этого столбца равна 1, а оставшиеся столбцы |
|
представляют собой выравнивание строк x[1i 1] и y[1j], причём оптимальное. А это в точности подзадача E[i 1, j], и она уже решена. Во втором случае стоимость последнего столбца также равна 1, и остаётся задача E[i, j 1]. В последнем же случае стоимость равна 1, если x[i] 6= y[j], и 0, если x[i] = y[j], а остаётся задача E[i 1, j 1]. Мы не знаем, какой из вариантов реально происходит в оптимальном выравнивании, поэтому проверим
все и выберем лучший: |
|
|
DRAFT |
||
E[i, j] = minf1 + E[i 1, j], 1 |
+ E[i, j 1], diff(i, j) + E[i 1, j 1]g, |
|
где diff(i, j) = 0, если x[i] = y[j], и 1 в противном случае. |
||
Например, для слов EXPONENTIAL и POLYNOMIAL подзадача E[4, 3] соот- |
||
ветствует префиксам EXPO и POL. Правый столбец их наилучшего выравни- |
||
вания может выглядеть одним из следующих способов: |
||
O |
|
O |
|
L |
L |
Поэтому E[4, 3] = minf1 + E[3, 3], 1 + E[4, 2], 1 + E[3, 2]g. |
||
Решения всех подзадач E[i, j] образуют двумерную таблицу (рис. 6.4). |
||
В каком порядке следует решать эти подзадачи? Подойдёт любой порядок, где E[i 1, j], E[i, j 1] и E[i 1, j 1] обрабатываются раньше, чем E[i, j]. Например, мы можем заполнять таблицу по строкам, сверху вниз, а внутри строки слева направо. Или, наоборот, по столбцам. В обоих случаях к тому времени, когда мы подойдём к вычислению очередной ячейки, требуемые для неё значения будут уже известны.
Рис. 6.4. (a) Таблица подзадач. Для вычисления значения E[i, j] необходимы значения E[i 1, j 1], E[i 1, j] и E[i, j 1]. (b) Заполненная таблица.
(a) |
|
|
|
|
|
|
|
|
|
(b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
j |
|
1 j |
|
|
n |
|
|
P |
O |
L |
Y |
N |
O |
M |
I |
A |
L |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
2 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
i |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
P |
3 2 3 3 4 5 6 7 8 9 10 |
|
||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
O |
4 3 2 3 4 5 5 6 6 8 9 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
5 |
4 |
3 |
3 |
4 |
4 |
5 |
6 |
6 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
6 |
5 |
4 |
4 |
4 |
5 |
5 |
6 |
6 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
7 |
6 |
5 |
5 |
5 |
4 |
5 |
6 |
6 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
8 |
7 |
6 |
6 |
6 |
5 |
5 |
6 |
6 |
8 |
9 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
цель |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
9 |
8 |
7 |
7 |
7 |
6 |
6 |
6 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
10 |
9 |
8 |
8 |
8 |
7 |
7 |
7 |
7 |
6 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
11 |
10 |
9 |
8 |
9 |
8 |
8 |
8 |
8 |
7 |
6 |
|
|
|
|
||||||||||||||||||||||||
|
|
Остаётся понять, с чего начинать (когда формула ещё не применима). |
||||||||||||||||||||||||
В данной задаче начальными значениями являются E[ , 0] и E[0, ] и за- |
||||||||||||||||||||||||||
полняются они очевидным образом: E[0, j] есть расстояние редактирования
162 |
Глава 6. Динамическое программирование |
между пустой строкой и первыми j символами из y, то есть j. Аналогично
E[i, 0] = i.
Теперь у нас всё готово для записи алгоритма.
для i от 0 до m:
E[i, 0] i
для j от 0 до n:
E[0, j] |
j |
|
для i от 1 до m: |
||
DRAFT6.4. Задача о рюкзаке |
||
для j от 1 |
до n: |
|
E[i, j] |
minfE[i 1, j] + 1, E[i, j 1] + 1, E[i 1, j 1] + diff(i, j)g |
|
вернуть |
E[m, n] |
|
Эта процедура заполняет таблицу построчно, слева направо в каждой строке. Обработка каждой ячейки занимает время O(1), поэтому общее время работы пропорционально размеру таблицы, то есть O(mn).
В рассмотренном нами ранее примере расстояние редактирования равно 6:
E X P |
O |
N E |
N |
– T |
I |
A |
L |
– – P |
O |
L Y |
N |
O M I |
A |
L |
|
Граф задачи и путь в нём
Мы уже говорили, что подзадачи можно рассматривать как вершины графа, в котором рёбра отражают зависимости между ними. В задаче нахождения расстояния редактирования вершинами можно считать клетки (i, j) таблицы, а рёбра соответствуют рекуррентной формуле:
(i 1, j) ! (i, j), (i, j 1) ! (i, j), (i 1, j 1) ! (i, j)
(см. рис. 6.5). Рёбрам этого графа можно так присвоить веса, что оптимальное расстояние редактирования будет равно длине кратчайшего пути. Для этого рёбрам типа (i 1, j 1) ! (i, j) при x[i] = y[j] (пунктирным) присвоим вес 0, а всем остальным –– вес 1. Ответом тогда будет просто длина кратчайшего пути из s = (0, 0) в t = (m, n). На рисунке показан один из таких путей. Он соответствует как раз оптимальному выравниванию, рассмотренному нами ранее. Каждый шаг вниз на этом пути соответствует удалению, вправо –– вставке, а по диагонали –– либо совпадению, либо замене.
Теперь видно, что точно так же можно решить и более общий вариант задачи о расстоянии редактирования, когда операции вставки, удаления и замены имеют не обязательно равные стоимости. Нам просто нужно будет изменить веса рёбер в этом графе.
Забравшийся в магазин вор нашёл больше добычи, чем он может унести с собой. Его рюкзак выдерживает не больше W килограммов. Ему надо выбрать

6.4. Задача о рюкзаке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
163 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 6.5. Граф выравнивания и путь длины 6. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
P |
O |
|
L |
|
Y |
|
N |
|
O |
|
M |
I |
|
A |
|
L |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E 





















 X
X 




















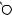


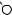
 P
P 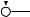
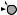



















 O
O 


















 N
N 











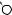


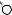


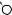


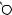


 E
E 
























 N
N 



















 T
T 




















 I
I 





















 A
A 





















 L
L 





















DRAFTЕсть две разновидности этой задачи. Если каждый товар имеется в неограниченном количестве, то оптимально будет взять товар номер 1 и две штуки товара номер 4 (общая стоимость: 48). Если же каждый товар есть в
какие-то из n товаров веса w1, , wn и стоимости v1, , vn. Как найти самый дорогой вариант?1
Пусть, например, рюкзак выдерживает W = 10 килограммов, а в магазине
имеются следующие изделия: |
|
|
Товар |
Вес |
Стоимость |
1 |
6 |
30 |
2 |
3 |
14 |
3 |
4 |
16 |
4 |
2 |
9 |
1Если этот пример кажется чересчур легкомысленным, несложно выбрать другие математически эквивалентные формулировки.
164 |
Глава 6. Динамическое программирование |
Часто используемые подзадачи
Включение задачи в семейство подзадач требует изобретательности –– но есть несколько стандартных вариантов.
ffВход –– последовательность x1, x2, , xn, подзадача –– тот же вопрос для префикса x1, x2, , xi для i < n.
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
|
DRAFT |
|||||||||
Количество таких подзадач линейно. |
|
|
|
|
||||||
ff Вход –– последовательности x1 |
, , xm и y1, , yn, подзадачи –– префиксы |
|||||||||
x1, , xi и y1, , yj для i < m |
и j < n. |
|
|
|
|
|||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
|
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
|
|
Количество подзадач есть O(mn).
ff Вход –– последовательность x1, , xn, подзадача –– участок xi , , x j для i < j < n.
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
Количество подзадач есть O(n2).
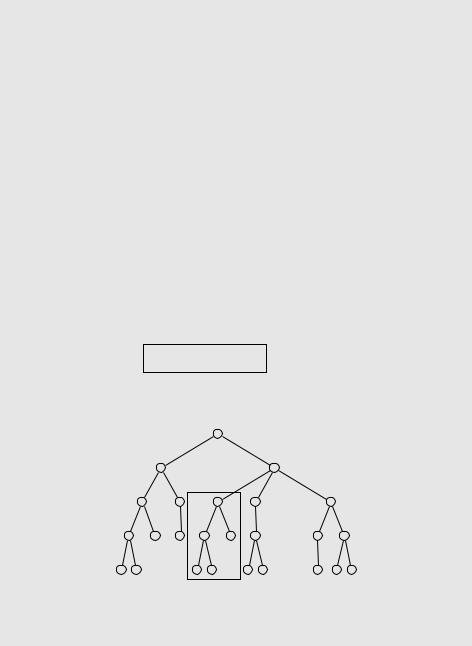
ff Вход –– корневое дерево, подзадача –– поддерево.
Сколько в этом случае будет подзадач?
Первые два случая нам уже встречались, скоро очередь дойдёт и до остальных.
единственном экземпляре (как в художественной галерее), тогда оптимальным будет набор из 1 и 3 (стоимость: 46).
В главе 8 мы увидим, что полиномиальных по времени алгоритмов для этих двух задач, скорее всего, не существует. Однако динамическое програм-
6.4. Задача о рюкзаке |
165 |
мирование позволяет решить обе задачи (в случае целых весов) за время O(nW ), которое вполне допустимо для малых W , но всё же не является полиномиальным, так как размер входа пропорционален log W , а не W .
Задача о рюкзаке с повторениями
Начнём с варианта с повторениями. Как обычно, важно правильно выбрать подзадачи. В данном случае есть два естественных способа: рассмотреть рюк-
зак меньшей ёмкости w ¶ W (для краткости максимально допустимый вес мы называем «ёмкостью») или же меньшее число товаров (скажем, товары 1, 2, , j, где j ¶ n). Для того чтобы понять, какой подход действительно работает, обычно приходится немного поэкспериментировать.
DRAFTгде, как обычно, максимум по пустому множеству считается равным 0. Получаем простой алгоритм:
Попробуем взять рюкзак меньшей ёмкости и положим
K[w] = максимально возможная стоимость для рюкзака ёмкости w.
Можем ли мы выразить K[w] через ответы для меньших подзадач? Ясно, что если в оптимальное заполнение рюкзака ёмкости w входит товар i, то без одной штуки этого товара мы получим оптимальное заполнение рюкзака ёмко-
сти w wi . Другими словами, K[w] –– это просто K[w wi ] + vi для некото- |
||||||||
рого i. Мы не знаем, для какого именно i, поэтому нам нужно перебрать все |
||||||||
возможные варианты: |
|
|
|
|
|
|
|
|
max |
K |
[ |
w |
|
w |
v |
i g |
, |
K[w] = i : wi ¶wf |
|
|
|
i ] + |
|
|||
K[0] 0
для w от 1 до W :
K[w] maxfK[w wi ] + vi : wi ¶ wg
вернуть K[W ]
Алгоритм последовательно заполняет массив размера W + 1. Значение каждой ячейки вычисляется за время O(n), общее время работы O(nW ).
Как обычно, данной задаче соответствует некоторый ориентированный ациклический граф на подзадачах. Решение исходной задачи можно свести к нахождению самого длинного пути в этом графе.
Задача о рюкзаке без повторений
Теперь рассмотрим вариант задачи, когда каждый товар есть в одном экземпляре. Тогда воспользоваться подзадачами из прошлого решения не удаётся, поскольку надо как-то учитывать, что мы уже взяли. Сделаем это, добавив второй параметр 0 ¶ j ¶ n: обозначим через K[w, j] максимальную стоимость унесённого, если разрешается уносить лишь товары 1, , j и общий вес должен быть не больше W . Исходная задача: найти K[W, n].
Теперь нужно научиться выражать K[w, j] через результаты для меньших подзадач. Это несложно. В оптимальном заполнении товар j либо участвует,

166 Глава 6. Динамическое программирование
О мышах и людях
В каждой живой клетке есть «программа» –– последовательность символов алфавита {A, C, G, T} (нуклеотидов), записанная в молекулах ДНК (дезоксирибонуклеиновой кислоты).
У любых двух людей последовательности ДНК (длиной примерно в 3 миллиарда символов) отличаются всего лишь на 0,1%. Но этих трёх миллионов различий достаточно, чтобы люди были совсем разные. Эти различия важны для биологии и медицины –– например, анализ ДНК может вы-
DRAFTявить предрасположенность к некоторым болезням.
ДНК –– огромная программа, с которой учёные только начинают разбираться. В ней есть участки с конкретными ролями (производство тех или иных белков), которые называют генами. При их обнаружении используются компьютеры, и эта область называется вычислительной геномикой. Как могут помочь тут наши алгоритмы?
1. При открытии нового гена в геноме человека один из способов понять его функцию –– найти похожие известные гены (возможно, у других хорошо изученных видов –– например, мышей). Слово «похожие» можно уточнять с помощью того или иного расстояния.
База данных GenBank, в которой хранятся известные гены, уже имеет общую длину более 1010 нуклеотидов и продолжает стремительно расти. Сейчас для поиска обычно используется программа BLAST, при создании которой понадобились и алгоритмические трюки, и биологическая интуиция.
2. При секвенировании ДНК (DNA sequencing), то есть определении последовательности символов, обычно разрезают молекулу на куски (подстроки) длиной 500––700 нуклеотидов и все их «читают». Допустим, мы нашли миллиарды таких случайно рассеянных по всей строке фрагментов, но как восстановить исходную последовательность? Ведь ни для одного из этих кусочков мы не знаем, с какой позиции он идёт. Это надо определить, склеивая перекрывающиеся фрагменты, и это была непростая задача. Первые «черновики» полной ДНК человека появились в 2001 году у двух групп: «Human Genome Consortium» (с государственным финансированием) и «Celera Genomics» (частная компания).
3. Когда некий ген найден у нескольких видов, можно ли использовать эту информацию для выяснения происхождения видов?
Мы рассмотрим эти вопросы в упражнениях в конце главы.
либо нет:
K[w, j] = maxfK[w wj , j 1] + vj , K[w, j 1]g
(первый член берётся, только если wj ¶ w.) Другими словами, можно выразить K[w, j] через результаты подзадач K[ , j 1].
Алгоритм заполняет двумерный массив из W + 1 строки и n + 1 столбца. Каждая ячейка заполняется за время O(1). Поэтому несмотря на гораз-

6.5. Произведение матриц |
167 |
до больший размер таблицы по сравнению с предыдущим алгоритмом общее время работы остаётся прежним: O(nW ).
для всех j, w: |
K[0, j] |
0; K[w, 0] 0 |
|
для j от 1 |
до n: |
|
|
для w от 1 до W : |
K[w, j 1] |
||
если wj > w: |
K[w, j] |
||
иначе: |
K[w, j] maxfK[w, j 1], K[w wj , j 1] + vj g |
||
вернуть K[W, n] |
|
|
|
6.5. Произведение матриц
Пусть нам необходимо вычислить произведение A B C D четырёх матриц размеров 50 20, 20 1, 1 10 и 10 100 (рис. 6.6). Для этого нужно умножать матрицы попарно в каком-то порядке. Как известно, матричное
Рис. 6.6. A B C D = (A (B C)) D.
(a) |
|
|
|
|
|
|
|
(b) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
B 1 10 |
|
|
|
|
|
B C |
|
|
|
||||||
|
A |
D |
|
A |
D |
|
||||||||||||
50 20 20 1 |
10 100 |
50 20 20 10 |
10 100 |
|
||||||||||||||
(c) |
|
|
|
|
|
|
|
(d) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A (B C) |
|
|
|
|
|
|
|
|
|||||||||
|
D |
|
|
|
|
(A (B C)) D |
|
|||||||||||
|
|
50 10 |
10 100 |
|
|
|
|
|
50 100 |
|
||||||||
умножение не является коммутативным (в общем случае A B 6= B A), но является ассоциативным (A (B C) = (A B) C). Таким образом, мы можем выбирать, в каком порядке перемножать матрицы (или, что то же самое, как расставить скобки). Важен ли тут порядок?
Обычная формула для произведения матриц m n и n p использует O(mnp) арифметических операций. Считая, что нужно ровно mnp операций, сравним несколько разных способов вычисления A B C D:
Порядок |
Подсчёт количества операций |
|
Количество операций |
|
|||
A ((B C) D) |
20 1 10 + 20 10 100 + 50 20 100 |
|
120200 |
(A (B C)) D |
20 1 10 + 50 20 10 + 50 10 100 |
|
60200 |
DRAFT(A B) (C D) 50 20 1 + 1 10 100 + 50 1 100 |
|
7000 |
|
Видно, что порядок умножения сильно влияет на итоговое количество операций. Более того, жадный алгоритм (выбирающий каждый раз две матрицы,

168 Глава 6. Динамическое программирование
Запоминание
Мы начинали с рекуррентной формулы, выражающей задачи большего размера через меньшие. Она использовалась для заполнения таблицы решений снизу вверх, от подзадач меньшего размера к большим´.
Как мы уже говорили, рекурсивный алгоритм, соответствующий рекуррентной формуле, может быть неэффективным, так как одни и те же подзадачи будут решаться снова и снова. Но его можно усовершенствовать, запоминая результаты предыдущих рекурсивных вызовов и используя их
DRAFTпри повторных вызовах с тем же входом.
В случае задачи о рюкзаке (с повторениями) такой алгоритм мог бы использовать хеш-таблицу (см. раздел 1.5) для хранения вычисленных ранее значений K[ ]. При запросе значения K[w] сначала проверялось бы, не присутствует ли оно уже в таблице, и только при его отсутствии производилось бы вычисление. Такой приём называется запоминанием (memoization).
{В хеш-таблицу помещаются значения K[w] (w –– в роли индекса).}
{Изначально таблица пуста.} функция Knapsack(w)
если w содержится в хеш-таблице:
вернуть K[w]
K[w] max{Knapsack(w wi ) + vi : wi ¶ w} добавить K[w] в хеш-таблицу с ключом w
вернуть K[w]
Этот алгоритм никогда не решает дважды одну подзадачу. Его время работы O(nW ), как и при использовании динамического программирования без запоминания. Но постоянный множитель, скрытый в O( ), при использовании рекурсии больше, чем в случае динамического программирования (из-за дополнительных проверок и накладных расходов при реализации рекурсии).
В некоторых случаях, однако, запоминание себя оправдывает. И вот почему: при динамическом программировании решаются все подзадачи, которые потенциально могли бы понадобиться, а при запоминании –– только те, которые реально понадобились. Например, пусть W и все веса wi кратны 100. Тогда подзадача K[w] бесполезна, если w не делится на 100. Рекурсивный алгоритм с запоминанием даже не будет рассматривать эти лишние клетки в таблице.
которые дешевле всего перемножить), приведёт нас ко второму варианту, далёкому от оптимума.
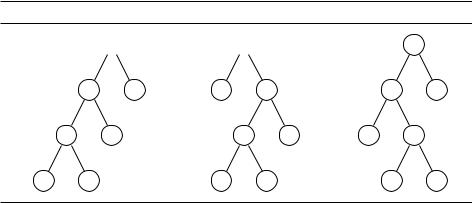
Как же найти оптимальный порядок перемножения матриц A1, A2, , An размеров m0 m1, m1 m2, , mn 1 mn соответственно? Порядок операций можно изобразить двоичным деревом, листьям которого будут соответствовать исходные матрицы, корню –– результат, а внутренним вершинам (у них
6.5. Произведение матриц |
169 |
два ребёнка) –– промежуточные результаты (рис. 6.7). Количество таких деревьев с n листьями зависит от n экспоненциально (упражнение 2.13), поэтому их перебирать долго.
Рис. 6.7. (a) ((A B) C) D. (b) A ((B C) D). (c) (A (B C)) D.
(a)  (b)
(b)  (c)
(c)
DRAFT |
D |
|||
D |
A |
|
|
|
C |
|
|
D A |
|
A B |
B |
C |
B C |
|
Вспомним, что поддеревья оптимального дерева оптимальны. Какие подзадачи соответствуют поддеревьям? Ими оказываются произведения Ai Ai+1 Aj . Следуя этой схеме, для 1 ¶ i ¶ j ¶ n положим
C[i, j] = минимальная стоимость вычисления Ai Ai+1 Aj .
Размер подзадачи –– это количество матричных операций, то есть j i. При i = j перемножать ничего не надо: C[i, i] = 0. При j > i рассмотрим оптимальное поддерево для вычисления C[i, j]. В двух его поддеревьях вычисляются
Ai Ak и Ak+1 Aj |
для некоторого k между i и j. Стоимость всего |
||||||||||||||||||
поддерева –– это сумма стоимостей двух частичных произведений и стоимо- |
|||||||||||||||||||
сти их перемножения: C[i, k] + C[k + 1, j] + mi 1 |
mk |
mj . Нам остаётся най- |
|||||||||||||||||
ти k, для которого эта стоимость окажется минимальной: |
|
j g |
|
||||||||||||||||
|
C[i, j] = i¶k<jf |
C |
[ |
i, k |
] + |
C |
[ |
k |
+ |
1, j |
] + |
m |
i 1 |
|
m |
k |
m |
. |
|
|
min |
|
|
|
|
|
|
|
|
|
|||||||||
Получаем такой алгоритм (в котором s –– размер подзадачи): |
|||||||||||||||||||
для i |
от 1 до n: C(i, i) |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для s |
от 1 до n 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для i от 1 до n s: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
i + s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C[i, j] minfC[i, k] + C[k + 1, j] + mi 1 mk mj : i ¶ k < jg
вернуть C[1, n]
Все подзадачи образуют двумерную таблицу. Вычисление значения каждой ячейки требует времени O(n). Поэтому общее время работы алгоритма есть O(n3).
170 |
Глава 6. Динамическое программирование |
6.6. Кратчайшие пути
Мы начали эту главу с простого алгоритма поиска кратчайшего пути в ориентированном ациклическом графе в качестве примера. Динамическое программирование полезно и в более сложных вариантах поиска кратчайших путей.
Кратчайшие надёжные пути
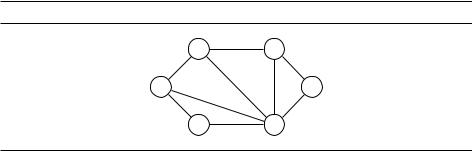
В практических задачах часто появляются разные дополнительные требования: супердешёвый маршрут с большим числом пересадок вряд ли нужен; пакет байтов, проходящий через большое число маршрутизаторов (даже очень быстрых), может потеряться. В таких ситуациях нужны пути, которые одновременно имеют малую длину (сумму длин рёбер) и малое количество рёбер. Скажем, в графе на рис. 6.8 кратчайший путь из вершины S в T состоит из
Рис. 6.8. Пути из S в T : длина и число рёбер.
A |
2 |
B |
|
|
|||
1 |
|
4 |
|
S |
5 |
1 T |
|
5 |
|||
2 |
1 |
||
|
|||
C |
3 |
D |
|
|
|
четырёх рёбер, в то время как существует немного более длинный путь, проходящий всего по двум рёбрам (и на практике он может быть лучше). Приходим к такой задаче:
Дан взвешенный граф G, вершины s и t и число k. Нужно найти кратчайший путь из s в t, проходящий не более чем по k рёбрам.
Можно ли приспособить алгоритм Дейкстры для этой задачи? Сложность в том, что алгоритм Дейкстры сосредоточен на длине кратчайшего пути и не заботится о числе рёбер.
Используя динамическое программирование, мы должны изобрести такие подзадачи, чтобы вся важная информация сохранилась для следующих этапов. В данном случае для каждой вершины v и каждого числа i ¶ k определим dist[v, i] как длину кратчайшего пути из s в v, проходящего не более чем по i рёбрам. Начальные значения dist[v, 0] бесконечны для всех вершин, кроме s, для которой dist[s, 0] = 0. Рекуррентная формула очевидна:
min |
u, i |
|
1 |
] + |
l u, v |
)g |
. |
dist[v, i] = (u,v)2Efdist[ |
|
|
( |
|
|||
Кратчайшие пути между всеми парами вершин |
|
|
|
||||
DRAFT |
|||||||
Пусть мы хотим найти кратчайшие пути не только между вершинами s и t, |
|||||||
а между всеми парами вершин. Можно запустить общий алгоритм нахождения кратчайших путей из пункта 4.6.1 (мы допускаем отрицательные рёбра)
