
Дасгупты, Пападимитриу, Вазирани «Алгоритмы»
.pdf
3.3. Поиск в глубину в ориентированных графах |
91 |
Тип ребра можно узнать по pre- и post-значениям его концов. Легко видеть, что вершина u является предком v тогда и только тогда, когда v была обнаружена во время вызова Explore(u). В этом случае pre[u] < pre[v] < < post[v] < post[u], то есть отрезок обработки v вложен в отрезок обработки u. Для обратных рёбер: u –– потомок v тогда и только тогда, когда v –– предок u; для перекрёстных рёбер u–v отрезки не пересекаются (и v-отрезок предшествует u-отрезку):
pre/post-отрезки для (u, v) |
типы рёбер |
|||
DRAFT |
||||
u |
v |
v |
u |
древесное/прямое |
v |
u |
u |
v |
обратное |
v |
v |
u |
u |
перекрёстное |
Понятно ли, почему не бывает других случаев расположения отрезков?
3.3.2. Ориентированные ациклические графы
Циклом (cycle) в ориентированном графе называется путь v0 ! v1 ! v2 ! ! vk ! v0 из некоторой вершины в неё же (по рёбрам). Скажем, в графе рис. 3.7 есть цикл B ! E ! F ! B и несколько других. Граф без циклов называется ациклическим (acyclic). Наличие циклов в ориентированном графе легко проверить с помощью одного вызова поиска в глубину.
Свойство. Ориентированный граф содержит цикл тогда и только тогда, когда при поиске в глубину обнаруживается обратное ребро.
Доказательство. Ясно, что если (u, v) –– обратное ребро, то путь в дереве поиска в глубину от v к u и само ребро (u, v) образуют цикл.
Обратно: пусть граф содержит цикл v0 ! v1 ! ! vk ! v0 и пусть vi –– вершина этого цикла, которая была обнаружена первой (то есть вершина цикла с минимальным pre[vi ]). Все оставшиеся вершины цикла достижимы из vi , и поэтому в дереве поиска в глубину они будут потомками vi . Тогда ребро vi 1 ! vi (или же vk ! v0, если i = 0) ведёт из вершины в её предка, то есть является обратным ребром. 

С помощью ориентированных ациклических графов (по-английски их называют directed acyclic graphs или сокращённо dags) удобно представлять временные и иерархические отношения, а также причинно-следственные связи. Допустим, к примеру, что необходимо сделать несколько вещей, причём есть ограничения на порядок (сначала надо проснуться и лишь потом встать с кровати; душ надо принять после того, как встал с кровати, но до того, как оделся). Как выбрать правильный порядок дел?

92 |
Глава 3. Декомпозиция графов |
Ограничения представим как ориентированный граф: каждому делу соответствует вершина; ребро из u в v означает, что u должно быть выполнено до v. Если в этом графе есть цикл, то правильного порядка не существует вовсе. Если же граф ациклический, то есть надежда его линеаризовать (linearize) или, как ещё говорят, топологически упорядочить (topologically sort) –– так упорядочить вершины, чтобы каждое ребро вело от более ранней вершины к более поздней. Например, для графа рис. 3.8 один из допустимых порядков таков: B, A, D, C, E, F. (Видите ли вы ещё три порядка?)
DRAFTКакие же ориентированные ациклические графы можно топологически упорядочить? Оказывается, что все, и это можно сделать с помощью поиска в глубину, расположив вершины в порядке убывания их post-значений. Ведь post(u) < post(v) только для обратных рёбер (u, v) (см. таблицу на c. 91), а мы уже знаем, что в ациклическом графе обратных рёбер быть не может:
Рис. 3.8. Ориентированный граф с одним источником, двумя стоками и четырьмя возможными линеаризациями.
A |
C |
E |
B |
D |
F |
Свойство. В ориентированном ациклическом графе каждое ребро идёт из вершины с б´ольшим post-значением в вершину с меньшим post-значением.
Посмотрим на первую и последнюю вершину после топологической сортировки. Из последней вершины рёбра не выходят: как говорят, она является стоком (sink). Напротив, в первую вершину рёбра не входят: как говорят, она является истоком (source). В частности, мы доказали такое утверждение:
Свойство. У каждого ациклического ориентированного графа есть хотя бы один исток и хотя бы один сток.
Это свойство (которое несложно доказать и без поиска в глубину) можно использовать для линеаризации: пока в графе есть вершины, надо искать исток, печатать его и удалять из графа. Понятно ли вам, почему такой алгоритм работает? Что будет, если в графе есть цикл? Как реализовать такой алгоритм за линейное время (упражнение 3.14)?
3.4. Компоненты сильной связности
3.4.1. Связность для ориентированных графов
Что означает связность для ориентированного графа? Тут надо быть аккуратным. Несвязный неориентированный граф можно разбить на связные компо-
3.4. Компоненты сильной связности |
93 |
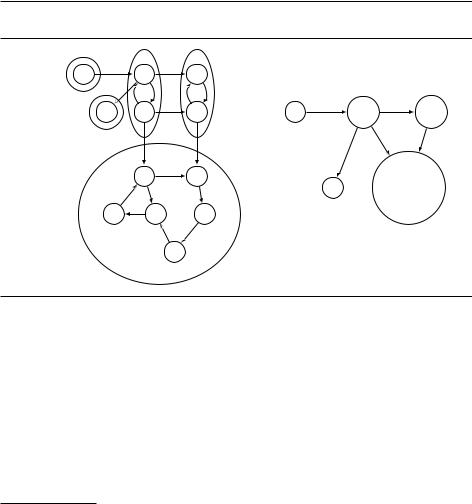
ненты, не соединённые друг с другом. С ориентированными графами ситуация сложнее. Граф рис. 3.9 нельзя разбить на две части, не соединённые друг с другом. Но мы не будем называть этот граф связным, поскольку в нём нет пути из G в B или из F в A. Дадим такое определение:
Вершины u и v ориентированного графа называются связанными (connected), если в нём есть путь из u в v, а также путь из v в u.
Такое отношение на вершинах разбивает все множество вершин на непересекающиеся подмножества (упражнение 3.30), называемые компонентами сильной связности (strongly connected components). Граф рис. 3.9 имеет пять таких компонент.
DRAFTСтянем теперь каждую компоненту сильной связности в отдельную вершину (метавершину) и оставим только рёбра между метавершинами (см. рис. 3.9), удалив дубликаты. Полученный граф называется метаграфом (meta-graph) исходного.1 Он не содержит циклов: если бы несколько компонент образовали цикл, то вершины этих компонент были бы в исходном графе достижимы друг из друга и вошли бы в одну компоненту.
Рис. 3.9. (a) Ориентированный граф и его компоненты сильной связности. (b) Метаграф.
(a) |
|
C |
(b) |
|
|
A |
B |
|
|
|
|
D |
E |
F |
A |
B, E |
C, F |
|
G |
H |
|
D |
G, H, I, |
|
|
|
|
J, K, L |
|
|
|
|
|
|
|
I |
J |
K |
|
|
|
|
|
L |
|
|
|
Свойство. Метаграф любого ориентированного графа является ациклическим (и может быть топологически упорядочен).
Но как построить метаграф для данного графа?
1В русской литературе такой граф называется также графом компонент или конденсацией исходного графа. –– Прим. перев.
94 |
Глава 3. Декомпозиция графов |
3.4.2. Алгоритм построения метаграфа
Компоненты сильной связности и метаграф могут быть построены за линейное время. Сейчас мы увидим, как это делается (и нам пригодится поиск в глубину). Начнём с такого замечания (уже нам известного).
Свойство 1. Процедура Explore, вызванная для вершины u, заканчивает работу, когда посещены все вершины, достижимые из u.
DRAFTЗначит, если вызвать Explore для вершины, которая лежит в компонен- те-стоке метаграфа, то мы обойдём как раз все вершины этой компоненты. Например, граф рис. 3.9 имеет две такие компоненты, и вызов Explore для вершины K обойдёт большую´ из них.
Остаётся понять, (а) как найти вершину, которая гарантированно лежит в компоненте-стоке, и (б) что делать после нахождения компоненты-стока.
Для начала ответим на первый вопрос. Сначала покажем, как решать симметричную задачу: найти вершину в компоненте-истоке.
Свойство 2. Вершина, которой поиск в глубину присваивает максимальное post-значение, лежит в компоненте-истоке.
Это вытекает из следующего более общего факта.
Свойство 3. Пусть C и C0 –– компоненты сильной связности графа и в графе есть ориентированное ребро из C в C0. Тогда максимальное post-значение вершин в C больше, чем максимальное post-значение вершин в C0.
Доказательство. Дождёмся момента, когда при поиске в глубину впервые появится вершина v из C или C0. Если v 2 C, то вызов Explore(v) не завершится, пока не будут обработаны все вершины обеих компонент (см. свойство 1). Поэтому post[v] будет больше, чем у всех вершин из C0. Если же v 2 C0, то вызов Explore(v) обойдёт все вершины C0, но до C дело ещё не дойдёт –– и максимальное post-значение в C тоже будет больше. 
Свойство 3 можно переформулировать так: компоненты сильной связности можно топологически упорядочить, расположив их по убыванию максимальных post-значений вершин в них. Это наблюдение обобщает рассмотренный нами алгоритм топологической сортировки ориентированных ациклических графов (в таких графах каждая компонента сильной связности состоит из одной вершины).
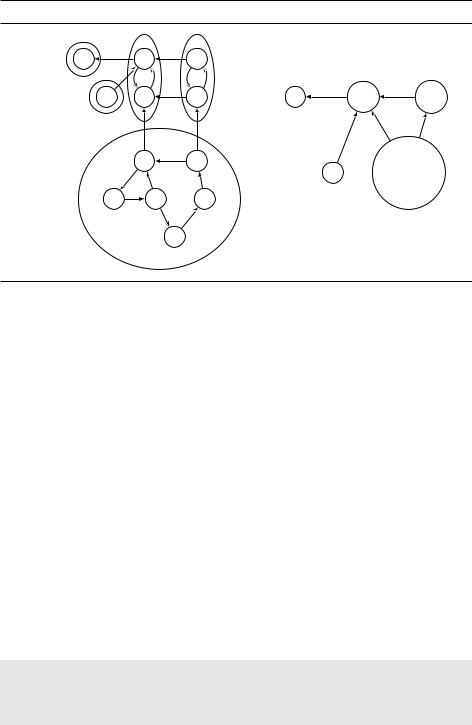
Свойство 2 позволяет найти нам вершину в компоненте-истоке графа, но нам хотелось бы иметь вершину в компоненте-стоке. Поэтому мы рассмотрим обращённый (reverse) граф GR, получаемый из G изменением направлений всех рёбер (см. рис. 3.10). У GR будут те же компоненты сильной связности, как и у G (почему?). Поиск в глубину на GR даст максимальное post-зна- чение для вершины из компоненты-истока графа GR, то есть для вершины из компоненты-стока графа G. Мы, таким образом, ответили на вопрос (а).
3.4. Компоненты сильной связности |
|
|
95 |
||
Рис. 3.10. Обращённый граф рис. 3.9. |
|
|
|
||
(a) |
|
C |
(b) |
|
|
A |
B |
|
|
|
|
D |
E |
F |
A |
B, E |
C, F |
DRAFT |
|||||
|
G |
H |
|
D |
G, H, I, |
|
|
|
|
|
J, K, L |
I |
J |
K |
|
|
|
L
Перейдём к вопросу (б). Как же находить следующую компоненту, когда компонента-сток уже найдена? В этом нам опять поможет свойство 3. Когда компонента вершины с максимальным post-значением найдена и удалена из графа, вершина с максимальным post-значением среди оставшихся вершин (имеются в виду уже вычисленные значения, мы не запускаем поиск повторно!) будет опять принадлежать компоненте-стоку в оставшемся графе, и так далее. Итоговый алгоритм прост:
1. Вызвать поиск в глубину для GR.
2. Вызвать алгоритм нахождения компонент связности в неориентированных графах (см. п. 3.2.3), перебирая в поиске в глубину вершины в порядке убывания их post-значений, найденных на первом шаге.
Время работы приведённого алгоритма линейно; он примерно вдвое медленнее поиска в глубину. (Разберитесь, как строить списки смежности графа GR и как упорядочить вершины по убыванию post-значений за линейное время.)
Опробуем этот алгоритм на графе рис. 3.9. Если на первом шаге вершины перебираются в алфавитном порядке, то убывание post-значений при поиске в глубину на GR идёт так: G, I, J, L, K, H, D, C, F, B, E, A. Второй шаг обнаруживает компоненты в таком порядке: fG, H, I, J, K, Lg, fDg, fC, Fg,
fB, Eg, fAg.
Быстрый обход веб-страниц
В этой главе мы предполагали, что граф дан нам в удобном виде: вершины пронумерованы от 1 до n, рёбра хранятся в списках смежности. Для веб-

96 Глава 3. Декомпозиция графов
графа всё гораздо сложнее: вершины заранее не известны, они обнаруживаются одна за другой в процессе поиска. И рекурсию использовать, конечно же, нельзя (глубина рекурсии будет слишком большой). Тем не менее для обхода веб-страниц используют алгоритмы, очень похожие на поиск в глубину. Поддерживается стек, содержащий все вершины, которые обнаружены (упоминаются в просмотренных ссылках), но пока не обработаны. В действительности это не совсем стек, поскольку первыми из него
достаются не те вершины, которые были помещены позже всех (и даже DRAFTне вершины, которые попали туда раньше всех, как при поиске в ширину,
см. главу 4). Первыми обрабатываются вершины, которые выглядят наиболее «интересными» (по каким-то эвристическим критериям). Это нужно, чтобы стек не переполнялся и чтобы в худшем случае необработанными остались только вершины, которые вряд ли бы привели к существенному расширению просмотренной области.
Обход веб-страниц обычно осуществляется несколькими компьютерами, вызывающими Explore параллельно: каждый из них снимает вершину со стека, скачивает соответствующую страницу и ищет в ней гиперссылки. Когда по ссылке находится новая страница, вместо рекурсивного вызова новая вершина просто помещается в стек (общий для всех компьютеров).
Один момент по-прежнему остаётся непонятным: когда находится новая страница, откуда мы знаем, что она действительно новая и что мы ещё не обрабатывали её? И какое имя мы даём ей (добавляем в стек и запоминаем как обработанное)? Это делается с помощью хеширования.
Кстати, оказалось, что алгоритмы нахождения сильно связанных компонент выявляют интересные свойства веб-графа.
Упражнения
3.1. Примените алгоритм поиска в глубину к данному графу, перебирая вершины в алфавитном порядке. Пометьте каждое ребро как древесное или обратное, а также вычислите pre- и post-значения для каждой вершины.
A B C
D E F
G H I
3.2. Примените алгоритм поиска в глубину к двум приведённым ниже графам, перебирая вершины в алфавитном порядке. Пометьте каждое ребро как древесное, прямое, обратное или перекрёстное, а также вычислите pre- и post-значения для каждой вершины.
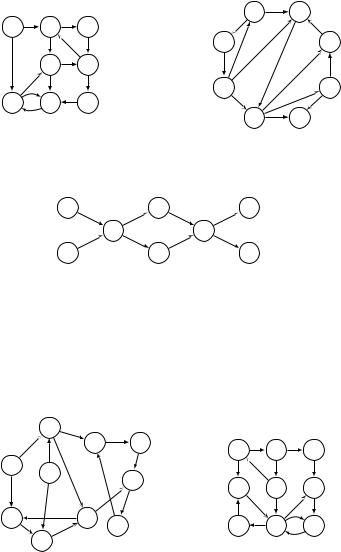
Упражнения |
97 |
(a) (b) |
A B |
A B C |
C |
H |
|
E D |
|
G |
D |
F G H |
F E |
|
|
DRAFT |
|
3.3. Примените алгоритм топологической сортировки, основанный на поиске в глубину, к следующему графу. Каждый раз в качестве следующей выбирайте первую в алфавитном порядке вершину.
A D G
C F
B E H
(a) Найдите pre- и post-значения всех вершин.
(b) Найдите все истоки и стоки графа.
(c) Какая линеаризация графа у вас получилась?
(d) Сколько различных линеаризаций есть у этого графа?
3.4. Примените алгоритм нахождения компонент сильной связности к следующим графам G. При поиске в глубину на GR в качестве следующей выбирайте первую в алфавитном порядке вершину.
(i) |
A |
|
|
|
(ii) |
|
|
|
C |
|
|
D |
A |
B |
C |
B |
|
|
|
|
|||
E |
|
F |
|
|
|
|
|
|
|
|
D |
E |
F |
||
|
|
|
|
||||
|
|
|
|
|
|||
G |
H |
J |
|
|
G |
H |
I |
|
|
|
|
I
(a)В каком порядке алгоритм находит компоненты сильной связности?
(b)Какие компоненты являются стоками и какие –– истоками?
(c)Нарисуйте метаграф (его вершинами являются компоненты сильной связности G).
(d)Какое минимальное число рёбер надо добавить, чтобы сделать граф сильно связным?
3.5. Обращённым графом для графа G = (V, E) называется граф GR = (V, ER) с теми же вершинами, рёбра которого получены изменением направления всех рёбер исходного графа: ER = f(v, u): (u, v) 2 Eg.
98 |
Глава 3. Декомпозиция графов |
|
Приведите линейный по времени алгоритм, который по заданному в виде |
списка смежности графу строит обращённый граф (тоже в виде списка смежности).
3.6. Степенью (degree) d(v) вершины v неориентированного графа G называется количество соседей v или, как говорят, инцидентных v рёбер. Для ори-
ентированных графов различают входящую степень (indegree) din(v) и исхо- |
||
дящую степень (outdegree) dout(v), то есть количество входящих в v и исходя- |
||
щих из v рёбер (соответственно). |
||
DRAFT |
||
|
|
(a) Докажите, что для неориентированного графа выполнено равенство |
u |
2 |
V d(u) = 2jEj. |
P (b) Выведите отсюда, что в неориентированном графе количество вершин |
||
нечётной степени чётно. |
||
|
|
(c) Верно ли это утверждение для вершин нечётной входящей степени в |
ориентированном графе? |
||
3.7. Граф G = (V, E) называется двудольным (bipartite), если множество его вершин можно разделить на две части (V = V1 [ V2 и V1 \ V2 = ?), так что все рёбра соединяют вершины из разных частей (например, если u, v 2 V1, то u и v не соединены ребром).
(a) Постройте линейный по времени алгоритм, определяющий, является ли входной граф двудольным.
(b) Определение двудольного графа можно давать разными способами. Например, граф является двудольным тогда и только тогда, когда его вершины можно корректно раскрасить в два цвета так, чтобы каждое ребро соединяло вершины разного цвета.
Докажите, что неориентированный граф является двудольным тогда и только тогда, когда в нём нет циклов нечётной длины.
(c) Сколько цветов понадобится, чтобы покрасить любой неориентированный граф, содержащий ровно один цикл нечётной длины?
3.8. Переливание воды. Есть три сосуда ёмкостью 10, 7 и 4 литров. Изначально первый сосуд пуст, а оставшиеся два полностью наполнены водой. За один ход разрешается переливать из одного сосуда воду в другой до тех пор, пока первый не станет пустым или же второй не заполнится до верха. Мы хотим проверить, существует ли последовательность ходов, в результате которой в одном из последних двух сосудов останется ровно два литра воды.
(a) Сформулируйте данную задачу как задачу о графах: определите соответствующий граф и переформулируйте вопрос в его терминах.
(b) Какой алгоритм нужно применить, чтобы ответить на данный вопрос?
(c) Найдите ответ, применив алгоритм.
3.9. Для вершины u неориентированного графа зададим twodegree[u] как сумму степеней соседей u. Покажите, как заполнить массив twodegree[ ] за линейное время для графа, заданного списком смежности.
Упражнения |
99 |
3.10. Перепишите процедуру Explore (рис. 3.3) без использования рекурсии. Процедуры Previsit и Postvisit должны вызываться в том же порядке, что в рекурсивной процедуре.
3.11. Укажите линейный алгоритм, который по данному ориентированному графу G и его ребру e определяет, есть ли в G цикл, содержащий e.
3.12. Докажите или опровергните: если fu, vg –– ребро неориентированного графа и post(u) < post(v), то v является предком u в дереве поиска в глубину.
DRAFT3.13. Связность неориентированных и ориентированных графов.
(a) Докажите, что в каждом связном неориентированном графе найдётся вершина, удаление которой оставляет граф связным. (Подсказка: рассмотрите дерево поиска в глубину графа.)
(b) Приведите пример сильно связного ориентированного графа, который перестаёт быть сильно связным при удалении любой вершины.
(c) Неориентированный граф, состоящий из двух компонент связности, всегда можно сделать связным, добавив одно ребро. Приведите пример ориентированного графа, состоящего из двух компонент сильной связности, из которого нельзя получить сильно связный граф добавлением одного ребра.
3.14. На с. 92 обсуждался альтернативный алгоритм топологической сортировки графа, который последовательно удаляет из графа истоки. Приведите линейную по времени реализацию такого алгоритма. (Подсказка: можно хранить входящие степени всех вершин и множество вершин нулевой входящей степени, корректируя эти данные по мере удаления вершин нулевой степени.)
3.15. (a) Власти сделали все дороги города односторонними и утверждают, что от любого перекрёстка по-прежнему можно добраться до любого другого, не нарушая правила. Как быстро их разоблачить? Сформулируйте данную задачу на языке графов и покажите, как её можно решить за линейное время.
(b) В ответ на претензии власти заявили, что имели в виду другое: куда бы ни поехать от мэрии по правилам, можно будет вернуться, не нарушая правил. Как проверить это утверждение за линейное время?
3.16. Магистерская программа по информатике состоит из n семестровых курсов. Граф G отражает зависимости: вершины графа соответствуют курсам, из v идёт ориентированное ребро в w, если w можно изучать только после v. Постройте линейный по времени алгоритм, который по G определяет минимальное количество семестров, необходимое для изучения всей программы (в одном семестре может быть сколько угодно курсов).
3.17. Бесконечные пути. Пусть дан ориентированный граф G = (V, E) с выделенной «начальной» вершиной s 2 V , а также множествами «хороших» вершин VG V и «плохих» вершин VB V . Бесконечным путём (infinite trace) в графе G называется бесконечная последовательность v0 v1 v2 вершин, в ко-
100 |
Глава 3. Декомпозиция графов |
торой v0 = s и (vi , vi+1) 2 E для всех i ¾ 0. В некоторых вершинах такой путь побывает бесконечно много раз.
(a) Через Inf(p) V обозначим те вершины бесконечного пути p, по которым путь проходит бесконечное число раз. Покажите, что Inf(p) целиком попадает в одну из компонент сильной связности графа G.
(b) Постройте алгоритм, определяющий, есть ли в G бесконечный путь.
(c) Постройте алгоритм, определяющий, есть ли в G бесконечный путь, проходящий через хорошие вершины бесконечно много раз.
DRAFT(d) Наконец, постройте алгоритм, проверяющий, существует ли бесконечный путь, который проходит бесконечное количество раз хотя бы по одной хорошей вершине, но по всем плохим вершинам проходит лишь конечное число раз.
3.18. Пусть двоичное дерево T = (V, E) задано списком смежности и указан корень дерева r 2 V . Напомним, что вершина дерева u называется предком вершины v, если путь от r до v в T проходит через u.
Мы хотим выполнить линейную предобработку дерева так, чтобы после этого была возможность отвечать на вопросы типа «является ли u предком v?» за время O(1). Возможно ли это?
3.19. Пусть опять дано дерево T = (V, E) с выделенным корнем, а также массив x[ ], содержащий по числу для каждой вершины дерева. Определим новый массив z[ ]:
z[u] = максимальное значение массива x на потомках u. Покажите, как заполнить такой массив за линейное время.
3.20. Дано дерево T = (V, E) с выделенным корнем r 2 V . Родителем вершины дерева v называется предпоследняя вершина на пути из r в v. Считаем также, что p(r) = r. Пусть p1(v) = p(v) и pk(v) = pk 1(p(v)) при k > 1. Другими словами, pk(v) –– это предок v в k-м поколении. Пусть также каждая вершина дерева v помечена положительным целым числом l[v]. Приведите линейный алгоритм, находящий новые метки lnew(v) = l(pl(v)(v)).
3.21.Постройте линейный алгоритм нахождения цикла нечётной длины в ориентированном графе. (Подсказка: рассмотрите сначала случай сильно связного графа.)
3.22.Постройте эффективный алгоритм, который определяет, есть ли в данном ориентированном графе вершина, из которой достижимы все вершины графа.
3.23.Постройте эффективный алгоритм, который по двум вершинам s, t 2 V ориентированного ациклического графа G = (V, E) находит количество различных путей из s в t.
3.24.Постройте линейный алгоритм, который проверяет, есть ли в данном
ориентированном ациклическом графе путь, проходящий через каждую вершину ровно один раз.
