
Дасгупты, Пападимитриу, Вазирани «Алгоритмы»
.pdf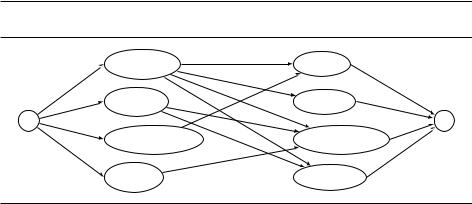
7.4. Принцип двойственности |
201 |
графе слева направо (рис. 7.8) и присвоим каждому ребру пропускную способность 1. Совершенное паросочетание существует тогда и только тогда, когда в этой сети имеется поток, размер которого равен числу пар. Понятно ли, почему? Можете ли вы найти такой поток в нашем примере?
Рис. 7.8. Сеть для поиска паросочетания. Пропускная способность каждого ребра равна единице.
DRAFT |
|
|
Андрей |
Анна |
|
Борис |
Белла |
|
s |
Вероника |
t |
Владимир |
|
|
Георг |
Галина |
|
Заметили ли вы тонкий момент в сказанном? Паросочетанию соответствует максимальный поток, но в обратную сторону нужен не просто поток, а целочисленный поток. (Вряд ли Анна может танцевать с Андреем на 70% и с Владимиром на 30%!)
К счастью, если все пропускные способности рёбер целочисленные, то найденный нашим алгоритмом оптимальный поток будет целочисленным. В самом деле, если все рёбра имеют целочисленную пропускную способность, то нецелым числам неоткуда взяться.
Это верно для любой сети: если пропускные способности рёбер целые, то оптимальное решение можно искать среди целочисленных (и наш алгоритм это делает). К сожалению, для задач линейного программирования это скорее исключение, чем правило: часто бывает, что для задачи с целочисленными ограничениями оптимум достигается только на нецелочисленных решениях. А если мы ограничимся только целочисленными решениями, то (как мы увидим в главе 8) поиск оптимального среди них –– и даже хоть какогонибудь целочисленного решения –– становится очень сложной задачей.
7.4. Принцип двойственности
Мы видели, что в сетях любой поток не превосходит любого разреза, и есть совпадающая пара (величина потока равна пропускной способности разреза). Найдя такую пару, мы тем самым убеждаемся, что в сети нет ни большего потока, ни меньшего разреза. Оказывается, что подобная удивительная вещь происходит вообще со всеми задачами линейного программирования: любая задача максимизации имеет двойственную задачу минимизации, и они связаны друг с другом примерно так же, как потоки и разрезы.
202 Глава 7. Линейное программирование
Чтобы понять, что это за двойственность, вспомним нашу первую линейную программу с двумя сортами шоколада:
x1 + 6x2 |
! max |
x1 |
¶ 200 |
x2 |
¶ 300 |
x1 + x2 |
¶ 400 |
DRAFT |
|
x1, x2 |
¾ 0 |
Симплекс-метод находит оптимальную точку (x1, x2) = (100, 300) со значением целевой функции 1900. Сразу же ясно, что этот вариант не так далёк от оптимума: сложив два первых неравенства (второе –– с коэффициентом 6), мы получим
x1 + 6x2 ¶ 2000,
так что выручка больше 2000 не получится. Можно ли сложить ограничения с другими коэффициентами (добавив пока не использованные, если надо) и получить лучшую оценку? Методом проб и ошибок можно найти, что сложение второго и третьего неравенств с коэффициентами 5 и 1 соответственно даёт
x1 + 6x2 ¶ 1900.
Таким образом, 1900 действительно оптимум! Этот магический приём подтверждения оптимальности мы уже обсуждали –– но по-прежнему неясно, всегда ли такое возможно, и если возможно, то как искать коэффициенты?
Чтобы ответить на этот вопрос, представим себе, что мы ещё не знаем этих коэффициентов, и обозначим эти неизвестные коэффициенты (при пер-
вых трёх неравенствах) через y1, y2, y3: |
|
|
Множитель |
Неравенство |
|
y1 |
x1 |
¶ 200 |
y2 |
x2 |
¶ 300 |
y3 |
x1 + x2 |
¶ 400 |
Во-первых, эти yi должны быть неотрицательными, иначе неравенство поменяло бы знак. Если это так, то мы получаем оценку
(y1 + y3)x1 + (y2 + y3)x2 ¶ 200 y1 + 300 y2 + 400 y3.
Во-вторых, мы хотим, чтобы левая часть совпала бы с целевой функцией x1 + 6x2, и тогда правая часть будет верхней оценкой для оптимального решения. Другими словами, нужно получить y1 + y3 = 1 и y2 + y3 = 6. Достаточно даже y1 + y3 ¾ 1 и y2 + y3 ¾ 6, поскольку тогда мы получим более сильное
7.4. Принцип двойственности |
|
|
203 |
неравенство.1 В итоге мы имеем оценку сверху: |
8 y1 |
|
|
x1 + 6x2 ¶ 200 y1 + 300 y2 + 400 y3 при |
+ y3 |
¾ 1 |
|
|
y1 |
, y2, |
y3 ¾ 0 |
|
< y2 |
+ y3 ¾ 6 |
|
|
: |
|
|
Как найти подходящие yi ? Можно попросту взять их достаточно большими, скажем, положить (y1, y2, y3) = (5, 3, 6). Но тогда оценка получится плохой (в нашем случае 200 5 + 300 3 + 400 6 = 4300). Чтобы оценка была как можно более точной, мы должны минимизировать 200 y1 +300 y2 +400 y3 при соблюдении указанных выше неравенств. Снова приходим к задаче линейного программирования:
DRAFTНа самом деле это не чудо, а закономерность –– подобную вещь можно проделать для любой задачи линейного программирования. Для удобства будем считать, что в ней используются только неотрицательные переменные,
200 y1 + 300 y2 + 400 y3 ! min
y1 + y3 |
¾ 1 |
y2 + y3 |
¾ 6 |
y1, y2, y3 |
¾ 0 |
Из построения следует, что всякое решение этой двойственной задачи даёт некоторую оценку сверху для исходной (прямой) задачи. Так что если мы ка- ким-то чудом нашли пару решений для той и другой задачи с совпадающими значениям, то оба они будут оптимальными. Вот такая пара для задачи про шоколад:
прямая: (x1, x2) = (100, 300); двойственная: (y1, y2, y3) = (0, 5, 1).
В обоих случаях получается 1900, так что оба решения оптимальны. Симво-
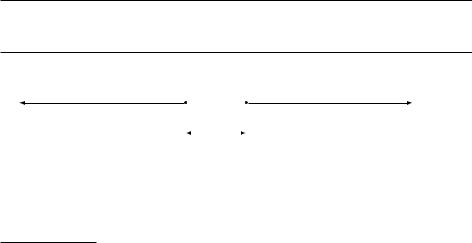
лически это изображено на рис. 7.9.
Рис. 7.9. Все значения для прямой задачи не превосходят значений для двойственной, так что первое множество лежит слева от второго. Вопрос только в том, есть ли между ними зазор –– и теорема о двойственности говорит, что нет.
оптимум |
оптимум |
|
|||||||
прямой |
двойственной |
значение |
|||||||
задачи |
задачи |
||||||||
целевой |
|||||||||
значения прямой задачи |
|
|
|
значения двойственной задачи |
|||||
|
|
|
функции |
||||||
|
|
|
|
|
|
||||
зазор (на |
|
|
|
|
|
|
нулевой) |
|
|
самом деле |
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1Это соответствует добавлению остававшихся без дела неравенств y1 ¶ 0 и y2 ¶ 0.

204 |
Глава 7. Линейное программирование |
а ограничения имеют вид неравенств. Вот как тогда строится двойственная задача:
ffВводим неопределённый коэффициент yj для каждого неравенства в прямой задаче; это будут (неотрицательные) переменные двойственной задачи.
ffДля каждой переменной xi в прямой задаче пишем неравенство (ограничение на yj ): при сложении неравенств прямой задачи (с множителями yj ) при xi должен получаться коэффициент, не меньший коэффициента в целевой функции прямой задачи.
ffЦелевой функцией двойственной задачи будет линейная комбинация коэффициентов yi , получающаяся в правой части при сложении неравенств прямой задачи с этими коэффициентами.
Поначалу это описание выглядит запутанным, но в матричной записи всё выглядит совсем просто (рис. 7.10). Более общий случай, когда среди условий есть и равенства, показан на рис. 7.11. Если прямая задача имеет огра- ничение-равенство, то соответствующий множитель (двойственная переменная) не обязан быть неотрицательным: равенства можно умножать на любые числа. Всё это выглядит довольно симметрично: в матрице A = (ai j ) каждому прямому ограничению соответствует строка, а каждому двойственному ––
столбец.
Рис. 7.10. Стандартная задача линейного программирования в матричной форме и её двойственная.
Прямая задача: |
Двойственная задача: |
|||||
|
T |
x ! max |
yT b |
min |
||
c |
|
y |
T ! |
|
T |
|
|
|
Ax ¶ b |
A ¾ c |
|
||
|
|
x ¾ 0 |
|
y ¾ 0 |
|
|
Рис. 7.11. В общем случае ограничения прямой задачи состоят из линейных неравенств (при i 2 I) и уравнений (при i 2 E), всего m = jIj+ jEj ограничений. Некоторые из n переменных x j (при j 2 N) обязаны быть неотрицательными. В двойственной задаче будет m = jIj+ jEj переменных. Те из них, которые соответствуют неравенствам, должны быть неотрицательными; остальные могут быть любыми.
Прямая задача: |
Двойственная задача: |
c1 x1 + + cn xn ! max |
b1 y1 + + bm ym ! min |
ai1 x1 + + ain xn ¶ bi для i 2 I |
a1 j y1 + + am j ym ¾ cj для j 2 N |
DRAFTai1 x1 + + ain xn = bi для i 2 E ai j y1 + + am j ym = cj для j 62N |
|
x j ¾ 0 для j 2 N |
yi ¾ 0 для i 2 I |

7.5. Игры с нулевой суммой |
205 |
Визуализация двойственности
Задачу о кратчайшем пути в неориентированном графе можно решать с помощью физической модели. Свяжем вершины графа верёвками по рёбрам, причём длину верёвки возьмём равной длине соответствующего ребра. Теперь для поиска кратчайшего пути из s в t достаточно потянуть за s и t в разные стороны: интуиция подсказывает, что натянутым окажется кратчайший путь из s в t.
DRAFT7.5. Игры с нулевой суммой |
|
B |
S A |
D |
C T |
Хотя этот процесс нагляден, в нём есть одна странность: задача о кратчайшем пути вообще-то является задачей минимизации, а в физической модели мы максимизируем расстояние между s и t. Отчего такая разница? Ответ: оттягивая s от t, мы решаем задачу, двойственную к задаче о кратчайшем пути! Эта двойственная задача имеет очень простой вид (упражнение 7.28) и использует по одной переменной xu на каждую вершину u:
xs xt ! max,
jxu xv j ¶ wuv для всех рёбер fu, vg.
Целевая функция соответствует желанию отдалить s от t, а ограничения соответствуют верёвкам, не дающим расстоянию между u и v превысить wuv .
По построению, каждое допустимое решение двойственной задачи даёт верхнюю оценку для всякого допустимого решения прямой. Оказывается, что их оптимумы совпадают!
Теорема о двойственности. Если линейная программа имеет ограниченный оптимум, то двойственная программа также имеет ограниченный оптимум, и они равны.
Мы не приводим доказательство этой теоремы. Скажем только, что если прямая программа описывает задачу о максимальном потоке, то двойственную линейную программу можно интерпретировать как задачу о минимальном разрезе (упражнение 7.25). Подобно тому, как алгоритм поиска максимального потока одновременно находил и минимальный разрез (и устанавливал их равенство), симплекс-метод может найти совпадающие оптимальные значения для прямой и двойственной задач, тем самым доказав утверждение теоремы.
Различные конфликтные ситуации из реальной жизни можно представить в виде матричных игр. Например, всем известная игра «камень-ножницы-бу-

7.5. Игры с нулевой суммой |
207 |
Мы видим, что если Строка следует выбранной стратегии, то ожидаемый платёж будет нулевым независимо от стратегии Столбца, так что у Строки есть гарантированный способ (в среднем) не проиграть. Для Столбца ситуация аналогична: равновероятная стратегия гарантирует ему нулевой ожидаемый платёж.
Что ж тут интересного –– ведь с самого начала было ясно, что игра в «ка- мень-ножницы-бумагу» симметрична? На самом деле мы доказали нечто большее. Представим себе, что Строка сначала объявляет свою стратегию, и Столбец знает об этом, делая свои ходы. Это, казалось бы, даёт ему преимущество по сравнению с вариантом, когда он сам объявляет свою стратегию (и Строка выбирает ответную стратегию после этого). Наш анализ показы-
DRAFTПусть Строка объявляет, что она будет использовать смешанную стратегию x = (1=2, 1=2). Что может сделать Столбец? Ход Н приведёт к ожидаемой потере 1=2, а ход С приведёт к ожидаемой потере 0. Таким образом, наилучшим ответным ходом Столбца будем чистая стратегия y = (0, 1).
вает, тем не менее, что такого преимущества для смешанных стратегий нет.
Это удивительное свойство верно для произвольных матриц платежей: оно следует из принципа двойственности в линейном программировании (на самом деле, эквивалентно ему). В качестве примера рассмотрим несимметричную игру. Представьте себе президентские выборы, в которых имеются два кандидата на пост, и каждый из них должен выбрать главную тему предвыборной кампании из двух вариантов (буквы обозначают экономику, общество, нравственность, снижение налогов). Элементы платёжной матрицы –– это миллионы голосов, теряемые Столбцом. (Мы предполагаем, что выбор те-
мы осуществляется до начала кампании и изменён быть не может.)
|
|
|
|
G = |
|
Н |
С |
Э |
3 |
1 |
|
|
О |
2 |
1 |
В общем случае, если фиксирована стратегия Строки x = (x1, x2), то всегда найдётся чистая стратегия, которая оптимальна для Столбца: либо делать ход Н с ожидаемым платежом 3x1 2x2, либо ход С с платежом x1 + x2, смотря по тому, какой меньше. Всякая смешанная стратегия y является взвешенным средним этих двух чистых стратегий, и поэтому не может побить лучшую из них.
Таким образом, если Строка должна объявить x до того, как сыграет Столбец, и рассчитывает на самый худший случай, в котором ожидаемый платёж равен minf3x1 2x2, x1 + x2g, то возникает такая оптимизационная задача:
выбрать (x1, x2), максимизирующее minf3x1 2x2, x1 + x2g
Этот выбор вероятностей xi даёт Строке лучшую из возможных гарантий ожидаемого платежа. Эту задачу можно записать в виде линейной программы, заметив, что для фиксированных x1 и x2 величину
z = minf3x1 2x2, x1 + x2g

208 |
Глава 7. Линейное программирование |
можно описать как максимальное значение в такой оптимизационной задаче:
z ! max
z¶ 3x1 2x2
z¶ x1 + x2
Вспоминая, что мы должны выбрать x1 и x2 так, чтобы максимизировать это z, получаем такую задачу:
DRAFTz ! max
3x1 + 2x2 + z ¶ 0 x1 x2 + z ¶ 0 x1 + x2 = 1 x1, x2 ¾ 0
Аналогично, если Столбец должен объявить первым о своей стратегии, то лучшее, что он может сделать, –– это выбрать смешанную стратегию y, минимизирующую его потери при лучшем ответе Строки. Другими словами, он
должен
выбрать (y1, y2), минимизирующее maxf3 y1 y2, 2 y1 + y2g .
| |
для неё |
{z |
} |
|
выигрыш Строки при наилучшем |
||||
В виде ЛП: |
|
|
ответе на y |
|
|
|
|
|
|
w ! min |
|
|
|
|
3 y1 + y2 + w ¾ 0 |
|
|
|
|
2 y1 y2 + w ¾ 0 |
|
|
|
|
y1 + y2 |
= 1 |
|
|
|
y1, y2 |
¾ 0 |
|
|
|
Теперь ключевым наблюдением является то, что эти две задачи являются двойственными друг для друга (см. рисунок 7.11)! Таким образом, они имеют одинаковый оптимум, назовём его V .
Что же у нас получилось? При помощи решения некоторой задачи линейного программирования Строка (максимизатор) может найти стратегию, которая гарантирует ей ожидаемый выигрыш не менее V , что бы ни делал Столбец. А при помощи решения двойственной ЛП Столбец (минимизатор) может гарантировать ожидаемый платёж не более V , что бы ни делала Строка. Такое значение V называется ценой (value) игры. В нашем случае цена игры равна 1=7, и она достигается смешанной стратегией (3=7, 4=7) для Строки, а также смешанной стратегией (2=7, 5=7) для Столбца.
Конкретный вид матрицы (и её размер) не играет роли –– мы фактически доказали (вывели из принципа двойственности в линейном программировании) фундаментальный результат теории игр, доказанный фон Нейманом и

7.6. Симплекс-метод |
209 |
называемый принципом минимакса (min-max theorem). Его можно записать в виде следующего равенства:
XX
max min |
Gi j xi yj = min max |
Gi j xi yj . |
x y |
y x |
i, j |
i, j |
|
Он показывает, что в случае смешанных стратегий открытое объявление используемой стратегии (в левой части это делает Строка, в правой –– Столбец) не даёт противнику преимущества: принцип двойственности (как и в случае максимальных потоков и минимальных разрезов) делает обе части равными.
DRAFT7.6. Симплекс-метод
Мы уже несколько раз упоминали «симплекс-метод» решения задач линейного программирования. Что же это такое?
Симплекс-метод получает набор линейных неравенств и линейную целевую функцию и находит оптимальную допустимую точку при помощи следующей стратегии:
v произвольная вершина допустимой области
пока у v есть сосед v0 с лучшим значением целевой функции: v v0
Слова «вершина» и «сосед» были понятны в наших двумерных и трёхмерных примерах (рис. 7.1 и 7.2). Что означают они для случая n переменных
x1, , xn?
Набор значений xi задаёт точку в векторном пространстве Rn. Линейное уравнение с n переменными x1, , xn задаёт гиперплоскость, разделяющую пространство на две части, а соответствующее линейное неравенство задаёт одну из этих частей –– полупространство (включая саму гиперплоскость, так как неравенства нестрогие). Наконец, множество допустимых решений линейной программы задаётся набором неравенств и поэтому представляет собой пересечение соответствующих полупространств –– выпуклый многогранник.1
Но что в нашем общем случае означают понятия вершина и сосед?
7.6.1. Вершины и соседи в n-мерном пространстве
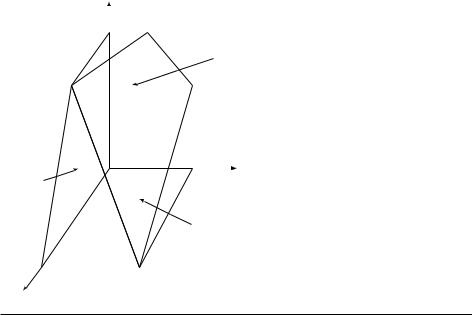
На рисунке 7.12 мы возвращаемся к уже встречавшемуся примеру. Если посмотреть на него внимательно, то мы видим, что каждая вершина может быть задана как единственная точка пересечения некоторого набора гиперплоскостей. Например, вершина A –– это единственная точка, в которой ограничения ○2 , ○3 и ○7 обращаются в равенства. С другой стороны, гиперплоскости, соответствующие неравенствам ○3 и ○6 , не задают (сами по себе, без третьей гиперплоскости) какую-либо вершину, так как их пересечение –– это не одна точка, а целая прямая.
1Точнее было бы говорить о выпуклой многогранной области: она может быть неограниченной (уходить в бесконечность), и такие пересечения полупространств обычно не считают многогранниками.
210 |
|
|
|
|
|
Глава 7. Линейное программирование |
|||||
|
|
|
|
|
|
|
|
|
|||
Рис. 7.12. Многогранник, заданный семью неравенствами. |
|
|
|
|
|||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
○2 |
|
7 |
|
x1 + 6x2 + 13x3 ! max |
|
||||
|
|
|
|
|
○ |
|
x1 |
¶ 200 |
○1 |
||
|
|
|
|
|
|
|
|||||
|
B |
|
|
C |
|
x2 |
¶ 300 |
○2 |
|||
|
|
|
|||||||||
|
|
|
|
|
|
|
x1 + x2 + x3 |
¶ 400 |
○3 |
||
|
|
|
3 |
|
|
x2 + 3x3 |
¶ 600 |
○4 |
|||
|
|
|
○ |
|
|
x1 |
¾ 0 |
○5 |
|||
|
|
|
|
○1 |
|
|
|||||
|
|
|
|
|
|
x |
|
¾ |
0 |
6 |
|
○5 |
|
|
|
x1 |
|
2 |
|
○ |
|||
|
|
|
|
|
|||||||
|
|
|
|
x3 |
¾ 0 |
○7 |
|||||
|
○4 |
|
|
○6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x3
Давайте превратим это в чёткое определение.
Выберем некоторое подмножество неравенств. Если существует единственная точка, в которой они обращаются в равенства, и эта точка допустима, то она называется вершиной.
Сколько уравнений требуется, чтобы однозначно задать точку? Когда имеется n переменных, нам нужно по крайней мере n линейных уравнений, если требуется единственное решение. С другой стороны, если уравнений больше n, то по крайней мере одно из них является линейной комбинацией других, а поэтому может не учитываться. Подытожим:
Каждая вершина задаётся множеством из n неравенств, обращающихся в ней в равенства.1
Теперь можно определить соседство.
Две вершины называются соседними, если они имеют n 1 общих определяющих неравенств.
Например, на рисунке 7.12 вершины A и C имеют общие определяющие неравенства {○3 ,○7 }, и поэтому они соседние.
|
1 |
|
|
|
DRAFTЗдесь есть тонкость: одна и та же вершина может порождаться различными подмножества- |
||||
ми неравенств. На рисунке 7.12 вершина |
B |
порождается подмножеством {○,○,○}, но также и |
||
|
|
|
2 3 4 |
|
{○2 ,○4 ,○5 }. Такие вершины называются вырожденными и требуют особого подхода. Мы рассмотрим эту ситуацию позже, а пока давайте считать, что вырожденных вершин в нашей задаче нет.
