Дасгупты, Пападимитриу, Вазирани «Алгоритмы»

ffМатериал 3 имеет плотность 3 тонны на кубический метр, всего доступно 20 кубических метров, доход –– 12000 руб. за кубический метр.

Напишите линейную программу, которая оптимизирует доход при имеющихся ограничениях.

7.4. Буфетчик решает, сколько «классического» и «крепкого» пива закупать в месяц. Классическое пиво обходится ему по десять рублей за литр, а продаёт он его по двадцать рублей за литр. Крепкое пиво обходится ему в пятнадцать рублей за литр, а продаётся по тридцать. Однако поставщик капризничает и DRAFTпродаёт литр крепкого только вместе с двумя литрами классического в нагрузку, и к тому же почему-то отказывается продавать больше 3000 литров (всего) в месяц. Как действовать буфетчику с наибольшей выгодой? (Раскупят в любом случае всё.) Составьте линейную программу и решите её геометрически.

7.5. Компания «Белый клык» предлагает два вида еды для собак: «Борзой щенок» и «Гончие псы», сделанные из смеси каши и мяса. На пакет «Борзого щенка» уходит 1 килограмм каши и 1,5 килограмма мяса; он продаётся за 70 рублей. Пакет «Гончих псов» использует 2 килограмма каши и 1 килограмм мяса и продаётся за 60 рублей. Каша стоит 10 рублей за килограмм, а мясо стоит 20 рублей за килограмм. Производственные расходы: 14 рублей на пакет «Борзого щенка» и 6 рублей на пакет «Гончих псов». Всего в месяц можно получить до 240 тонн каши и 180 тонн мяса. Покупают всё произведённое. На производстве есть «узкое место» –– за месяц фабрика может упаковать только 110000 пачек «Борзого щенка». Естественно, руководство желает максимизировать доход.

(a) Сформулируйте задачу в виде линейной программы с двумя переменными.

(b) Изобразите множество допустимых решений, запишите координаты каждой вершины и отметьте вершину с максимумом дохода. Чему равен этот максимум?

7.6. Приведите пример линейной программы с двумя переменными, у которой область допустимых значений бесконечна, но имеется оптимальное решение (с конечным значением целевой функции).

7.7. Укажите все пары вещественных чисел a, b, при которых линейная программа

x + y ! max ax + b y ¶ 1 x, y ¾ 0

(a) несовместна;

(b) не ограничена;

(c) имеет единственное оптимальное решение.

7.8. Даны следующие точки на плоскости:

(1, 3), (2, 5), (3, 7), (5, 11), (7, 14), (8, 15), (10, 19).

Вам нужно найти прямую ax + b y = c, которая приблизительно проходит через эти точки (никакая прямая в точности не подойдёт). Напишите линейную программу (решать её не нужно) для поиска прямой, минимизирующей

максимальное абсолютное отклонение (maximum absolute error)

7.9. Задача квадратичного программирования состоит в максимизации квадратичной целевой функции (с членами вроде 3x2 или 5x1 x2) с учётом набо-

1

ра линейных ограничений на переменные. Приведите пример такой задачи с двумя переменными x1, x2, для которой допустимая область значений переменных непуста и ограничена, но никакие вершины этой области не оптимизируют (квадратичную) целевую функцию.

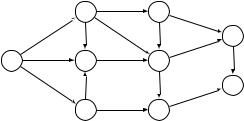
7.10. Для следующей сети с указанными пропускными способностями рёбер найдите максимальный поток из S в T , а также соответствующий разрез.

7.11.Рассмотрим такую задачу линейного программирования: x + y ! max

2x + y ¶ 3

x+ 3 y ¶ 5 x, y ¾ 0

Какая задача будет к ней двойственной? Найдите оптимальные решения для прямой и для двойственной задач.

7.12.Для линейной программы

x1 2x3 ! max x1 x2 ¶ 1

2x2 x3 ¶ 1 x1, x2, x3 ¾ 0

докажите, что решение (x1, x2, x3) = (3=2, 1=2, 0) оптимально.

7.13. Орлянка. В этой игре с двумя участниками один из игроков зажимает рублёвую монету в кулак орлом или решкой вверх, а второй пытается отгадать, орёл сверху или решка. Если отгадал, он забирает монету, а если нет –– платит рубль штрафа.

(a) Представьте платежи в виде матрицы размера 2 2.

(b) Какова цена этой игры и каковы оптимальные стратегии для каждого из игроков?

ют со следующей недели разные новшества. Джонни предполагает либо понизить цены, либо увеличить порции. У Тони есть три варианта: начать выпускать пиццу лучшего качества, поставить столики на улице или предлагать газировку бесплатно. Комбинации этих вариантов приведут к таким результатам (указан выигрыш Джонни, равный убытку Тони):

Какова цена этой игры и каковы оптимальные стратегии для игроков? 7.15. Найдите цену игры, заданной следующей матрицей платежей:

(Подсказка: рассмотрите смешанные стратегии (1=3, 0, 0, 1=2, 1=6, 0, 0, 0) и (2=3, 0, 0, 1=3).)

7.16. В салат входят (1) помидоры, (2) салат-латук, (3) шпинат, (4) морковь,

(5) масло. Каждая порция салата должна содержать (A) по крайней мере 15 г белков, (B) не менее 2 г и не более 6 г жиров, (C) по крайней мере 4 г углеводов, (D) не более 100 мг натрия. Содержание этих веществ (в расчёте на 100 г продукта) приведено в таблице. Кроме того, (E) ваш салат не должен содержать больше 50% зелени (салата-латука и шпината) от общей массы.

Найдите в интернете программу для решения задач линейного программирования и используйте её, чтобы найти вариант с наименьшим количеством калорий при заданных ограничениях. Объясните, как вы составляли линейную программу и каково оптимальное решение (количество каждого ингредиента и значение калорийности). Укажите использованные источники.

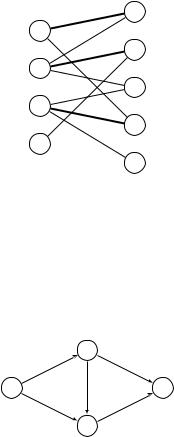
7.17. Рассмотрите следующую сеть (числа обозначают пропускные способности рёбер).

ми его рёбер). На этой остаточной сети отметьте вершины, достижимые из S, и вершины, из которых достижима T .

(c) Ребро сети называется узким местом (bottleneck edge), если увеличение его пропускной способности приводит к увеличению максимального потока. Перечислите все узкие места для сети выше.

(d) Приведите простой пример (не больше четырёх вершин) сети без узких мест.

(e) Приведите эффективный алгоритм поиска всех узких мест в сети. (Подсказка: начните с запуска обычного алгоритма поиска максимального потока, а затем исследуйте остаточную сеть.)

7.18. Известно много вариаций задачи о максимальном потоке. Вот четыре

(a)Имеется несколько истоков и несколько стоков, и нам нужно максимизировать общий поток из всех истоков во все стоки.

(b)Каждая вершина также имеет пропускную способность –– максимальный поток, который может в неё входить.

(c)Каждое ребро имеет не только пропускную способность, но и нижнюю оценку на проходящий через него поток.

(d)Исходящий поток из каждой вершины u не совпадает с входящим, а получается из него умножением на (1 "u), где "u –– коэффициент потерь для вершины u.

Укажите эффективные алгоритмы для этих задач, сведя (a) и (b) к обычной задаче о максимальном потоке, а (c) и (d) –– к задаче линейного программирования.

7.19. Пусть кто-то утверждает, что нашёл максимальный поток в некоторой сети. Постройте линейный по времени алгоритм, проверяющий, действительно ли данный поток максимален.

7.20. Рассмотрим следующее обобщение задачи о максимальном потоке. Дана ориентированная сеть G = (V, E) с пропускными способностями рё-

бер fceg. Вместо одного истока и одного стока даны несколько пар (s1, t1), (s2, t2), ‌, (sk, tk), где si –– это истоки, а ti –– стоки. Также дано k чисел d1, ‌ ‌, dk. Нужно найти k потоков f (1), ‌, f (k) со следующими свойствами:

ff f (i) является потоком из si в ti .

ffДля каждого ребра e суммарный поток fe(1) + fe(2) + ‌ + fe(k) не превосходит пропускную способность ce.

ff Величина каждого потока f (i) не меньше di .

ff Величина общего потока (суммы потоков) максимальна. Как бы вы решали эту задачу?

7.21.Ребро в сети называется критическим, если уменьшение его пропускной способности приводит к уменьшению максимального потока. Приведите эффективный алгоритм, который находит в сети какое-нибудь критическое ребро.

7.22.В сети G = (V, E), рёбра которой имеют целочисленные пропускные способности ce, мы уже нашли максимальный поток f из вершины s в вершину t. Однако только что мы узнали, что одно из использованных значений пропускной способности было неверным: для ребра (u, v) мы использовали cuv , хотя надо было cuv 1. Это досадно, потому что поток f использовал именно это ребро на полную мощность: fuv = cuv .

Можно было бы повторить заново всё вычисление потока, но есть более быстрый метод. Покажите, как новый оптимальный поток можно вычислить за время O(jV j + jEj).

7.23.Вершинным покрытием неориентированного графа G =(V, E) называется множество его вершин, которое покрывает каждое ребро, то есть подмножество S V с таким свойством: для каждого ребра fu, vg 2 E хотя бы один из его концов u, v лежит в S.

Покажите, что задача нахождения минимального вершинного покрытия в двудольном графе сводится к задаче о максимальном потоке. (Подсказка: можете ли вы как-то связать минимальное вершинное покрытие с минимальным разрезом в некоторой сети?)

7.24.Алгоритм для двудольного паросочетания без сведения к потоку. Мы уже знаем, как искать максимальное паросочетание в двудольном графе при помощи сведения к задаче о максимальном потоке. Теперь мы разработаемDRAFT

прямой алгоритм.

Пусть G = (V1 [ V2, E) –– двудольный граф (рёбра идут между V1 и V2), и пусть M E –– некоторое паросочетание в G (то есть множество рёбер, не имеющих общих концов). Вершина называется покрытой паросочетанием M, если она является концом одного из рёбер M. Чередующимся путём (alternating path) называется путь нечётной длины, который начинается и заканчивается в непокрытых вершинах и рёбра которого поочерёдно принадлежат M и E M.

двойственное решение, стоимость которого в точности равна пропускной способности этого разреза.

7.26. В совместной системе линейных неравенств

a11 x1 + ‌ + a1n xn ¶ b1,

. . . . . . . . . . . . . . . . . . . . . . . . .

am1 x1 + ‌ + amn xn ¶ bm

мы называем j-е неравенство вынужденным равенством (forced-equal), если оно обращается в равенство для всякого допустимого решения x =(x1, ‌, xn). Другими словами, P aji xi ¶ bj не является вынужденным равенством, если

существует некотороеi x, которое удовлетворяет всем ограничениям, и при этом P aji xi < bj .

i

Например, в случае

x1 + x2 ¶ 2,

x1 x2 ¶ 2, x1 ¶ 1,

x2 ¶ 0

первые два неравенства являются вынужденными равенствами, а третье и четвёртое –– нет.

Решение x системы неравенств называется характеристическим (characteristic), если для всякого неравенства I, не являющегося вынужденным равенством, x удовлетворяет I, не обращаясь в равенство. В примере выше таким решением является (x1, x2) = ( 1, 3), для которого x1 < 1 и x2 < 0, в то время как x1 + x2 = 2 и x1 x2 = 2.

(a) Покажите, что всякая совместная система имеет характеристическое решение.

(b) Покажите, как при помощи линейного программирования можно узнать, какие неравенства в данной совместной системе являются вынужденными равенствами, и найти характеристическое решение.

7.27. Покажите, что задача о размене монет (упражнение 6.17) может быть сформулирована как целочисленная линейная программа. Можем ли мы решать соответствующую задачу линейного программирования, будучи уверенными, что решение окажется целочисленным (как в случае двудольного паросочетания)? Докажите это или приведите контрпример.

7.28. Линейная программа для кратчайшего пути. Пусть мы хотим найти

(b) Запишите задачу о кратчайшем пути в виде линейной программы.

(c) Покажите, что двойственную линейную программу можно записать в виде

xs xt ! max

xu xv ¶ luv для всех (u, v) 2 E.

(d) Мы уже обсуждали двойственную программу для задачи о кратчайшем пути на с. 205. В чём разница между теперешней двойственной программой и тогдашней?

7.29. Голливуд. Кинопродюсер ищет актёров и инвесторов для своего нового фильма. Есть n актёров; i-й актёр согласен сниматься за si долларов. Есть также m инвесторов; j-й инвестор предоставляет pj долларов, но с условием, что все актёры из определённого множества Lj f1, 2, ‌, ng будут сниматься в фильме.

Выручка продюсера –– это сумма выплат инвесторов минус выплаты актёрам. Цель всякого продюсера –– максимизировать выручку.

(a) Сформулируйте это в виде задачи целочисленного программирования, в которой переменные принимают значения из множества f0, 1g. (Введите переменную xi для участия i-го актёра и переменную yj для участия j-го спонсора. Как записать условия с помощью неравенств вида yj ¶ xi ?)

(b) Покажите, что возникающая линейная программа в действительности имеет целочисленное оптимальное решение (как и в случае с максимальным потоком и паросочетанием в двудольном графе), и что нецелое оптимальное решение (найденное с помощью линейного программирования) легко преобразовать в целое. (Подсказка: те переменные, которые не равны нулю или единице, можно все вместе сдвигать, пока одна из них не упрётся в край, так мы уменьшаем число нецелых значений, сохраняя оптимальность.)

7.30. Теорема Холла. Возвратимся к танцам из раздела 7.3. Предположим, что у нас имеется двудольный граф с каким-то количеством мальчиков слева и таким же количеством девочек справа. Теорема Холла утверждает, что совершенное паросочетание существует тогда и только тогда, когда для любых k мальчиков есть по крайней мере k девочек, соединённых с кем-то из выбранных k мальчиков.

Докажите эту теорему. (Подсказка: можно воспользоваться теоремой Фор- да––Фалкерсона.)

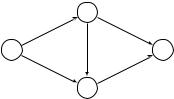
7.31. Рассмотрите следующую простую сеть с указанными пропускными способностями рёбер.

(a) Покажите, что если запустить для этого графа алгоритм Форда––Фал- керсона, то неразумный выбор путей в остаточной сети может привести к тысяче итераций! (Представьте себе, что было бы, если бы пропускные способности были равны миллиону.)

Сейчас мы укажем способ выбирать пути, при котором алгоритм гарантированно останавливается за разумное число итераций.

Рассмотрим произвольную ориентированную сеть G = (V, E), s, t, fceg, в которой мы хотим найти максимальный поток. Предположим, что все про- DRAFTпускные способности рёбер –– целые числа, не меньшие 1, и назовём пропускной способностью пути из s в t наименьшую пропускную способность рёбер этого пути. Самым широким (fattest) путём из s в t назовём путь с наибольшей пропускной способностью.

(b) Покажите, что самый широкий путь из s в t можно найти с помощью (модифицированного) алгоритма Дейкстры.

(c) Покажите, что максимальный поток в G есть сумма отдельных потоков вдоль не более чем jEj путей из s в t.

(d) Теперь покажите, что если мы всегда увеличиваем поток вдоль самого широкого пути в остаточной сети, то алгоритм Форда––Фалкерсона нахождения максимального потока остановится не более чем за O(jEj log F) итераций, где F –– размер максимального потока. (Подсказка: полезно вспомнить доказательство теоремы о жадном покрытии множествами в разделе 5.4.)

На самом деле, ещё более простой подход –– построение пути в остаточном графе при помощи поиска в ширину –– гарантирует, что потребуется не более O(jV j jEj) итераций.

Глава 8

NP-полные задачи

DRAFT8.1. Задачи поиска

В семи предыдущих главах мы рассмотрели алгоритмы поиска кратчайших путей и минимальных покрывающих деревьев, паросочетаний в двудольных графах, максимальных возрастающих последовательностей, максимальных потоков в сетях и так далее. Все эти алгоритмы эффективны в том смысле, что с ростом длины входа (n) время работы растёт не быстрее, чем полином (скажем, n, n2 или n3) от n.

Чтобы понять, в чём тут достижение, заметим, что во всех этих задачах решение (путь, дерево, последовательность) ищется среди экспоненциального числа кандидатов. Действительно, есть n! способов разбить n девочек и n мальчиков на пары, в полном графе с n вершинами есть nn 2 покрывающих деревьев, в графе обычно есть экспоненциальное число путей из s в t. Поэтому если просто пробовать все варианты, то получится алгоритм с экспоненциальным временем работы, скорее всего бесполезный на практике (см. следующую врезку). Эффективному алгоритму, таким образом, необходимо каким-то хитрым способом избежать такого полного перебора, используя свойства решаемой задачи.

Мы уже рассмотрели приёмы, позволяющие в некоторых случаях избежать экспоненциального перебора: жадные алгоритмы, динамическое программирование, линейное программирование (а вот метод «разделяй и властвуй», как правило, лишь ускоряет решение задач, которые и без него

От Сиссы до Мура

Легенда говорит, что брамин Сисса, придумав шахматы, показал их начальству (королю) –– которое игру одобрило и предложило выбрать награду. Брамин скромно попросил положить одну рисинку на первую клетку доски, две –– на вторую, четыре –– на третью и так далее, удваивая количество вплоть до шестьдесят четвёртой клетки. Король неосторожно согласился и вошёл в историю как первая жертва экспоненциального роста («комбинаторного взрыва»): запрошенное количество риса, 264 1 = 18 446 744 073 709 551 615 зёрен, в тысячи раз превосходит годовой урожай риса во всей Индии! Это не просто байки: скажем, бактерии (при отсутствии ограничений) тоже размножаются экспоненциально. В 1798 году английский философ Томас Роберт Мальтус предсказал, в со-