
Дасгупты, Пападимитриу, Вазирани «Алгоритмы»
.pdf
5.1. Покрывающие деревья |
131 |
Рис. 5.3. В неориентированном графе (a) выбрано множество рёбер X (b) и некоторый разрез (c), который не пересекают рёбра из X . Ребро e –– одно из минимальных рёбер, пересекающих этот разрез. Не всякое минимальное покрывающее дерево T , содержащее X , содержит e –– но в T можно заменить одно из рёбер на e, получив минимальное покрывающее дерево T 0, содержащее X [ feg.
(a) |
1 |
3 |
|
A |
|||
C |
E |
DRAFT |
|
||||||||
|
|
2 |
|
2 |
|
2 |
3 |
2 |
|
|
|
|
B |
1 |
D |
|
4 |
F |
|
(b) |
C |
|
|
|
|
|
|
C |
|
A |
|
|
E |
|
|
A |
E |
||
рёбра X : |
|
|
|
|
|
T : |
|
|
|
B |
D |
|
|
F |
|
|
B |
D |
F |
(c) |
C |
|
|
|
|
|
|
C |
|
A |
|
|
E |
|
|
A |
E |
||
разрез: |
|
e |
|
|
|
T 0: |
|
|
|
B |
D |
|
|
F |
|
|
B |
D |
F |
|
S |
|
V S |
|
|
|
|
|
|
Для этого используется система непересекающихся множеств (disjoint sets); эти множества будут компонентами связности текущего графа. Изначально каждая вершина составляет отдельную компоненту, и мы создаём соответствующие множества с помощью операции
MakeSet(x): создать одноэлементное множество fxg.
Мы проверяем, лежат ли множества в одной компоненте, сравнивая коды соответствующих компонент; эти коды даёт нам процедура
Find(x): какое множество содержит x?
При добавлении ребра, связывающего вершины x и y, мы объединяем две компоненты с помощью процедуры
Union(x, y): объединить множества, содержащие x и y.
Если нам позволено обращаться к структуре данных, реализующей такие операции, то алгоритм Крускала записать легко (рис. 5.4). Он использует jV j операций MakeSet, 2jEj операций Find и jV j 1 операцию Union.
132 |
Глава 5. Жадные алгоритмы |
Рис. 5.4. Алгоритм Крускала построения минимального покрывающего дерева.
процедура Kruskal(G, w)
{Вход: связный неориентированный граф G = (V, E)
с весами рёбер we.}
{Выход: X –– минимальное покрывающее дерево (множество рёбер).}
для всех вершин u 2 V :
MakeSet(u)
DRAFTПомимо родительского указателя каждая вершина также имеет ранг, о котором позже.
X fg
упорядочить рёбра множества E по весу
для всех рёбер fu, vg 2 E в этом порядке: если Find(u) 6= Find(v):
добавить ребро fu, vg к X
Union(u, v)
5.1.4. Непересекающиеся множества: реализация
Объединение по рангу
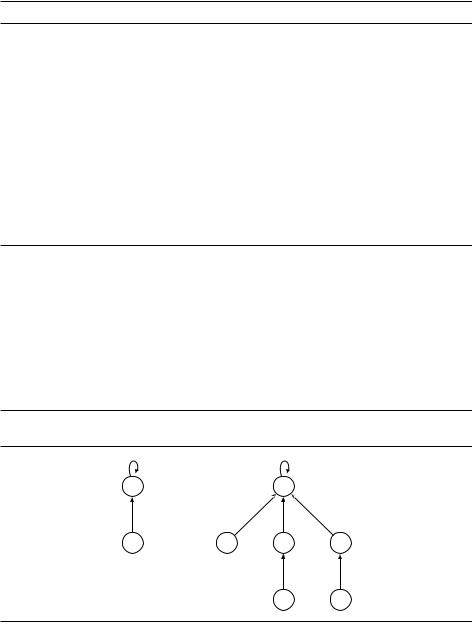
Один из способов хранения множества –– ориентированное дерево (рис. 5.5). Вершины этого дерева –– элементы множества. Каждая вершина, кроме корня, хранит также указатель на родителя; корень хранит указатель на самого себя. Корень дерева можно рассматривать как код, или представитель (representative), соответствующего множества.
Рис. 5.5. Представление множеств fB, Eg и fA, C, D, F, G, Hg в виде ориентированных деревьев.
E |
|
H |
|
B |
C |
D |
F |
|
|
G |
A |
процедура MakeSet(x)
(x) x rank(x) 0

5.1. Покрывающие деревья |
133 |
функция Find(x)
пока x 6= (x): x (x)
вернуть x
Как и следовало ожидать, операция MakeSet занимает время O(1). А операция Find проходит по родительским указателям к корню, поэтому занимает время, пропорциональное высоте дерева. Строится дерево в ходе опера-
ции Union, которую надо спроектировать так, чтобы по возможности избегать высоких деревьев.
DRAFTПример использования этих операций показан на рис. 5.6.
Чтобы объединить два множества (два дерева), можно найти их корни и
в одном из них поставить ссылку на другой. Тут есть произвол (какой из корней выбрать). Чтобы высота росла медленнее, логично подвешивать более низкое дерево к более высокому. В этом случае высота увеличивается, только если объединяемые деревья имеют одинаковую высоту. Но как узнать высоту? Её можно хранить (и поддерживать при операции соединения) в корне, в поле rank. Этот подход называется объединением по рангу (union by rank).1
процедура Union(x, y) |
|
|
||
rx |
Find(x) |
|
|
|
ry |
Find(y) |
|
|
|
если |
rx = ry : |
ничего делать не надо, выходим |
||
если rank(rx ) > rank(ry ): |
|
|
||
(ry ) rx |
{объявляем rx |
родителем |
ry } |
|
иначе: |
|
|
|
|
(rx ) ry |
{иначе наоборот} |
|
||
если rank(rx ) = rank(ry ): |
rank(rx ) |
rank(ry ) + 1 |
||
Последние две строки алгоритма корректируют информацию о высотах поддеревьев, когда это необходимо (когда соединяются деревья одинаковой высоты). По индукции легко проверить, что в поле ранга rank всегда будет храниться высота поддерева, растущего из этой вершины. В частности, при подъёме к корневой вершине значения ранга возрастают:
Свойство 1. Если x 6= (x), то rank(x) < rank( (x)).
Дерево с рангом k получается только при объединении двух деревьев ранга k 1. По индукции отсюда следует (проверьте):
Свойство 2. Каждая корневая вершина ранга k имеет по меньшей мере 2k вершин в своём дереве.
Это верно и для внутренних (не корневых) вершин: вершина ранга k имеет по меньшей мере 2k потомков (считая её саму). Действительно, при соеди-
1На самом деле нам будет полезно иметь такое поле не только для корней, но и для всех вершин. Видно, что в процедуре Union в её нынешнем варианте в каждой вершине в поле rank остаётся высота поддерева, висящего под ней –– которая перестаёт меняться, как только вершина перестала быть корнем. –– Прим. ред.
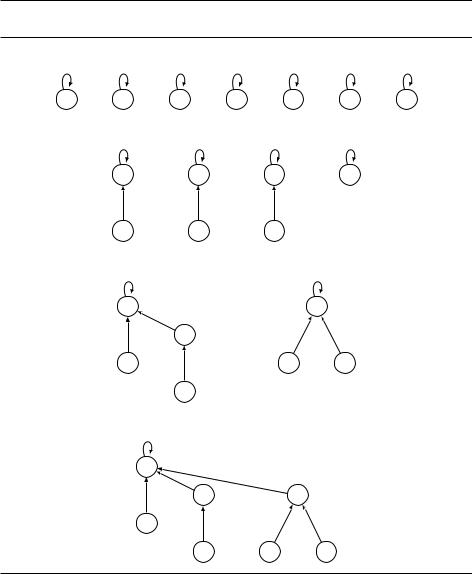
134 Глава 5. Жадные алгоритмы
Рис. 5.6. Последовательность операций для системы непересекающихся множеств. Ранги обозначены верхними индексами.
После MakeSet(A), MakeSet(B), , MakeSet(G):
A0 |
B0 |
C0 |
D0 |
E0 |
F0 |
G0 |
После Union(A, D), Union(B, E), Union(C, F): |
|
|
||||
DRAFT |
||||||
|
D1 |
|
E1 |
F1 |
G0 |
|
|
A0 |
|
B0 |
C0 |
|
|
После Union(C, G), Union(E, A): |
|
|
D2 |
|
F1 |
E1 |
|
|
A0 |
C0 |
G0 |
B0 |
|
|
После Union(B, G): |
|
|
D2 |
|
|
E1 |
F1 |
|
A0 |
|
|
B0 |
C0 |
G0 |
нении двух деревьев у их внутренних вершин не меняются ни ранги, ни потомки, а для корня, становящегося внутренней вершиной, это свойство мы уже знаем. Заметим ещё, что различные вершины ранга k не могут иметь общих потомков, потому что по свойству 1 всякий элемент имеет не более одного предшественника ранга k.
Свойство 3. Если всего элементов n, то имеется не более n=2k элементов
ранга k.
5.1. Покрывающие деревья |
135 |
В частности, ранг любой вершины не больше log2 n. Таким образом, все деревья имеют высоту не более log2 n, и получается оценка сверху на время работы Find и Union.
Сжатие путей
Теперь мы можем оценить время работы алгоритма Крускала. Сортировка
рёбер |
займёт время O( E |
j |
log |
j |
V |
) (напомним, что log |
j |
E |
j |
= O(log |
j |
V |
), так как |
|
2 |
j |
|
j |
|
|
|
j |
|
||||||
jEj ¶ jV j |
). Столько же уйдёт на объединение и поиск в оставшейся части ал- |
|||||||||||||
горитма. Казалось бы, нет смысла улучшать нашу структуру данных. |
||||||||||||||
DRAFT |
||||||||||||||
Однако это всё же может иметь смысл. Представим себе, что данные нам рёбра уже упорядочены по весу и на это тратить время не надо. Или, допустим, все веса невелики (например, O(jEj)), и тогда сортировку можно сделать за линейное время. В таких случаях «узким местом» становится структура данных, и полезно задуматься об улучшении её производительности, тем более что это совсем несложно, а наша структура данных полезна и в других ситуациях.
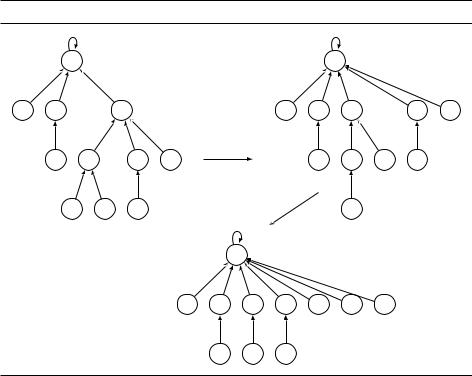
В чём состоит улучшение? Как по ходу дела упростить себе будущую работу? В ходе каждого вызова Find мы проходим от вершины к корню –– так почему бы нам тут же не прицепить все эти вершины к корню, чтобы не повторять путь в следующий раз? Этот трюк со сжатием путей (path compression)
показан на рис. 5.7; |
он лишь немного увеличивает время работы операции |
|||||||
Рис. 5.7. Сжатие путей. Показаны результаты вызовов Find(I) и Find(K). |
||||||||
A3 |
|
|
|
|
|
|
A3 |
|
B0 C1 |
E2 |
|
|
|
B0 |
C1 |
E2 |
F1 I0 |
D0 |
F1 |
G1 |
H0 |
|
|
D0 |
G1 |
H0 J0 |
I0 |
J0 |
K0 |
|
|
|
|
K0 |
|
|
|
|
|
A3 |
|
|
|
|
|
|
|
B0 C1 |
E2 |
F1 |
I0 |
K0 |
G1 |
|
|
|
D0 |
H0 |
J0 |
|
|
|

136 Глава 5. Жадные алгоритмы
Find и легко программируется с помощью рекурсивной процедуры
функция Find(x)
если x 6= (x):
(x) Find( (x))
вернуть (x)
Преимущество этой простой модификации проявляется в долгосрочной перспективе, а не мгновенно, поэтому требует особого анализа: мы долж-
DRAFTны рассмотреть последовательности операций Find и Union. Эта амортизированная стоимость (amortized cost) оказывается немногим больше O(1) и значительно улучшает нашу предыдущую оценку O(log n).
Почему на каждый запрос в среднем (почти) хватает одной операции? Ведь некоторые операции Find вполне могут быть долгими? Выполняя такую операцию, мы заодно перевешиваем все проходимые нами вершины сразу под корень, так что второй раз долгой операции с ними не будет. Значит, количество действий, посвящённых данной вершине, будет небольшим. (Тут есть тонкость: вершина, подвешенная к корню, впоследствии может оказаться в глубине дерева, когда этот корень будет соединён с другими корнями, и снова получится долгая операция. Но это, как мы сейчас увидим, бывает редко и на среднее влияет мало.)
Выделим в нашей структуре «верхний уровень», состоящий из корней деревьев, и «нижний уровень», состоящий из внутренних вершин. Существует разделение труда: операции Find (со сжатием путей или без него) затрагивают только внутренние вершины деревьев, в то время как операции Union (после того как мы уже нашли корни соединяемых деревьев с помощью Find) обращаются только к верхнему уровню. Таким образом, сжатие путей никак не влияет на набор корней и на то, какие вершины подчинены данному корню.
Сжатие путей не меняет ранги, но меняет деревья, так что ранг уже не обязан совпадать с высотой поддерева. Заметим, что как только некоторая вершина перестаёт быть корнем, она навсегда остаётся внутренней и её ранг зафиксирован. Таким образом, ранги всех вершин не меняются при сжатии путей, хоть эти числа больше не могут быть интерпретированы как высоты поддеревьев. В частности, свойства 1––3 (с. 133) остаются в силе.1
Если имеется n элементов, их ранги лежат в отрезке от 0 до log n по свойству 3. Разделим ненулевую часть этого интервала на некоторые специально подобранные части (из соображений, которые станут ясны позже):
f1g, f2g, f3, 4g, f5, 6, , 16g, f17, 18, , 216 =65536g, f65537, , 265536g,
Каждая из этих частей имеет вид fk + 1, k + 2, , 2kg, где k –– степень двойки. Количество частей равно log n, то есть числу последовательных операций log, которые необходимо применить к n, чтобы получить число, не пре-
1Тут надо быть аккуратным. Свойство 2 теперь верно лишь для корневых вершин ранга k (они образуются, когда соединяются две вершины ранга k 1). В дальнейшем вершина ранга k может стать внутренней, и при сжатии путей потерять кого-то из своих детей. Но в любом случае эти дети не используются при образовании новых вершин ранга k, так что свойство 3 остаётся в силе. –– Прим. ред.

5.1. Покрывающие деревья |
137 |
Вероятностный алгоритм для задачи о минимальном разрезе
Мы уже говорили о связи между покрывающими деревьями и разрезами. Вот другой пример. Удалим последнее ребро, которое алгоритм Крускала
добавляет к покрывающему дереву; дерево разделится на две компоненты и получится разрез ( , ¯). Что можно сказать про этот разрез? Пред-
S S
положим, что все веса рёбер одинаковые, а порядок рёбер (в алгоритме
Крускала) случайный. Тогда с вероятностью по крайней мере 1=jV j2 разрез ( , ¯) является минимальным (минимально число рёбер, проходящих
DRAFTвосходящее единицы. Например, log 1000 =4, так как log log log log 1000 ¶1. На практике будут использоваться только первые пять из указанных интервалов; больше требуется только при n ¾ 265536, то есть никогда.
S S
¯ |
2 |
между S и S). Повторив это O(jV j ) раз (каждый раз выбирая порядок рё- |
|
бер случайно) и взяв минимальный из найденных разрезов, мы с большой вероятностью (скажем, 99%, или любой другой, если взять подходя-
щую константу в O(jV j2)) получим минимальный разрез в G. Тем самым получается вероятностный алгоритм со временем работы O(jEjjV j2 log jV j)
для невзвешенных минимальных разрезов. Улучшенный вариант этого алгоритма, имеющий время работы O(jV j2 log jV j), построил Дэвид Каргер (David Karger), и это самый быстрый из известных сейчас алгоритмов.
Почему разрез последнего шага будет минимальным с вероятностью по меньшей мере 1=jV j2? На каждом шаге множество вершин разбито на компоненты связности. Вершины, добавляемые к дереву, соединяют разные компоненты. Количество рёбер, инцидентных каждой компоненте, не меньше C (размера минимального разреза в G), поскольку они соответствуют другому разрезу. Когда осталось k компонент, число пригодных к добавлению рёбер не меньше kC=2 (из каждой из k компонент исходит по меньшей мере C рёбер, но надо учесть двойной подсчёт каждого ребра). Можно считать, что на каждом шаге алгоритма мы выбираем случайное ещё не рассмотренное ребро, так что следующее возможное ребро из списка будет входить в минимальный разрез с вероятностью не более C=(kC=2) = 2=k. Таким образом, с вероятностью 1 2=k = (k 2)=k выбор и на следующем шаге не затронет минимального разреза. Поэтому вероятность того, что алгоритм Крускала так и не затронет минимальный разрез
вплоть до последнего ребра покрывающего дерева, по меньшей мере
jV j 2 |
|
jV j 3 |
|
jV j 4 |
|
|
|
2 |
|
1 |
= |
2 |
. |
|
jV j |
jV j 1 |
jV j 2 |
|
4 |
3 |
|
|
jV j(jV j 1) |
|
|||||
Разные вызовы операции Find занимают разное время. Мы оценим среднее время работы при помощи хитрой бухгалтерии. А именно, каждой вершине мы дадим определённое количество денег, так что в сумме окажется роздано не более n log n рублей. Затем мы покажем, что каждый вызов Find занимает O(log n) шагов плюс некоторое дополнительное время, которое можно «оплатить» деньгами задействованных вершин, по рублю за единицу времени. Таким образом, среднее время для m вызовов Find рав-

138 |
Глава 5. Жадные алгоритмы |
но O(m log n) (непосредственно учтённое) плюс не более O(n log n) за счёт вершин.
Более точно, вершина получает свои деньги, как только она перестаёт быть корнем; в этот момент её ранг фиксируется. Если этот ранг попадает в интервал fk + 1, , 2kg, то вершина получает 2k рублей. По свойству 3 количество вершин ранга больше k не превышает
n + n + ¶ n .
2k+1 2k+2 2k
DRAFTПопулярной альтернативой алгоритму Крускала является алгоритм Прима, в котором X является множеством рёбер некоторого поддерева, а S –– множество вершин рёбер из X .
Таким образом, общая сумма, выданная вершинам из данного интервала, не превышает n рублей, и так как всего интервалов log n, то общая розданная
сумма ¶ n log n.
Время выполнения операции Find пропорционально (для простоты считаем –– равно) количеству переходов от сына к отцу. При этом ранги возрастают, и в какие-то моменты переходят из группы в группу по нашей классификации. Таких переходов границы не более log n (понимаете, почему это так?). Эти переходы и дают O(log n) шагов, а остальные нужно оплатить за
счёт вершин.
При переходе процедуры Find от ребёнка к родителю (если их ранги в одной группе, см. выше) ребёнок платит рубль. При той же операции Find происходит сжатие путей, так что этот ребёнок переусыновляется родителем более высокого ранга. Так может повторяться несколько раз для одного и того же ребёнка –– но хватит ли у него денег? Пока ранг родителя будет оставаться
в той же группе, что ранг ребёнка, хватит: внутри группы fk + 1, , 2kg будет меньше 2k шагов. А после этого (когда родители будут из старших групп) за
переходы денег у вершин не берут по правилам оплаты.
Это завершает доказательство оценки O(log n) для среднего времени вы-
полнения последовательности операций в расчёте на одну операцию.
5.1.5. Алгоритм Прима
Вернёмся к обсуждению алгоритмов для минимального покрывающего дерева. Свойство разреза показывает, что достаточно следовать такой (жадной) стратегии:
X fg {выбранные на данный момент рёбра} повторять:
выбрать множество S V , для которого X не имеет рёбер
между S и V S
e 2 E |
ребро минимального веса между S и V S |
X |
X [ feg |
пока jX j ¶ jV j 1 |
|
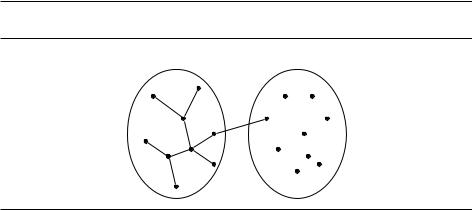
На каждом шаге к дереву добавляется одно ребро, а именно, ребро наименьшего веса среди рёбер, соединяющих S и его дополнение (рисунок 5.8).
5.2. Кодирование Хаффмана |
139 |
Рис. 5.8. Алгоритм Прима: рёбра множества X образуют дерево, а множество S состоит из вершин этого дерева.
S |
V S |
|
X |
e |
|
DRAFT |
||
Другими словами, на каждом шаге к S добавляется вершина v 62S |
минималь- |
|
ной стоимости в смысле такого определения:
cost(v) = min w(u, v).
u2S
Это сильно напоминает алгоритм Дейкстры, и на самом деле псевдокод (рисунок 5.9) практически тот же. Единственное различие в том, как задаются приоритеты в очереди. В алгоритме Прима приоритет вершины v определяется значением cost[v], то есть минимальным весом ребра из S в v, в то время как в алгоритме Дейкстры мы сравнивали полные длины путей, а не только их последние рёбра. Но на времени работы это не сказывается (оно зависит от выбранной реализации очереди с приоритетами).
На рисунке 5.9 показана работа алгоритма Прима на маленьком графе с шестью вершинами. Результирующее дерево задаётся массивом указателей на родителя (prev).
5.2. Кодирование Хаффмана
Как получаются mp3-файлы?
1. Звуковой сигнал (точнее, соответствующий электрический сигнал) измеряется через фиксированные промежутки времени. В идеале эти измерения можно считать последовательностью вещественных чисел s1, s2, , sT . (Например, при частоте 44100 измерений в секунду, как это принято для ком- пакт-дисков, 50-минутная симфония требует T = 50 60 44100 130 миллионов измерений. Реально большинство записей происходят в режиме «стерео» и два канала дают вдвое больше измерений.)
2. Точность измерения ограничена, так что st квантуется (quantize) и получается число из некоторого конечного множества . (Желательно выбирать это множество аккуратно, чтобы на слух воспроизведённый сигнал был похож на исходный).
3. Полученная последовательность длины T из элементов кодируется битами.
140 |
Глава 5. Жадные алгоритмы |
Рис. 5.9. Вверху: алгоритм Прима для построения минимального покрывающего дерева. Внизу: пример работы алгоритма, запущенного из вершины A. Показаны значения массивов cost/prev и построенное дерево.
процедура Prim(G, w)
{Вход: связный неориентированный граф G = (V, E) с весами рёбер we.} {Выход: минимальное покрывающее дерево, заданное массивом prev.}
для всех вершин u 2 V : |
|
|
|
|
|
|
|
|
|
|||||||||||
DRAFT |
|
|
||||||||||||||||||
cost[u] |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
prev[u] nil |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
выбрать произвольную начальную вершину u0 |
|
|
|
|
|
|
||||||||||||||
cost[u0] |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
H MakeQueue(V ) {в качестве ключей используются значения cost} |
|
|||||||||||||||||||
пока H не пусто: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
v DeleteMin(H) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
для всех рёбер fv, zg 2 E: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
если z 2 H и cost[v] > w(v, z): |
|
|
|
|
|
|
|
|||||||||||
|
|
|
cost[z] w(v, z) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
prev[v] v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
DecreaseKey(H, z, cost[z]) |
|
|
|
|
|
|
|
||||||||||
|
A |
|
6 |
|
C |
|
|
|
5 |
|
|
E |
A |
|
|
C |
|
|
E |
|
5 |
|
4 |
1 |
|
|
2 |
3 |
|
4 |
|
|
|
|
|
|
|
||||
|
B |
|
2 |
|
D |
|
|
|
4 |
|
|
F |
B |
|
|
D |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Множество S |
|
|
|
A |
|
B |
C |
D |
|
E |
|
F |
|
|||||
|
|
|
|
{} |
|
|
|
|
|
0/nil |
|
1/nil |
1/nil |
1/nil |
1/nil |
1/nil |
|
|||
|
|
|
|
A |
|
|
|
|
|
|
5=A |
6=A |
4=A |
1/nil |
1/nil |
|
||||
|
|
|
A, D |
|
|
|
|
|
|
2=D |
2=D |
|
1/nil |
4=D |
|
|||||
|
|
|
A, D, B |
|
|
|
|
|
|
|
|
1=B |
|
1/nil |
4=D |
|
||||
|
|
|
A, D, B, C |
|
|
|
|
|
|
|
|
|
|
|
5=C |
3=C |
|
|||
|
|
|
A, D, B, C, F |
|
|
|
|
|
|
|
|
|
|
|
4=F |
|
|
|
||
|
|
A, D, B, C, F, E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
||||||||||||||||||
|
|
На последнем шаге используется кодирование Хаффмана. Объясним его |
||||||||||||||||||
на простом примере. Пусть, скажем, надо закодировать слово из 130 миллионов букв алфавита = fA, B, C, Dg. Можно каждую букву кодировать двумя битами (A как 00, , D как 11) –– понадобится 260 мегабитов. А короче нельзя?
