2.2. Марковские процессы.

Однородные цепи Маркова представляют собой частный случай марковских процессов, а именно – марковские процессы с дискретным временем. В этом пункте мы изучим основные свойства марковских процессов с непрерывным временем.

Определение. Случайный процесс ξ(t) называется марковским, если для любого момента времени t₁ при известном значении ξ(t₁) случайные величины ξ(t) с t > t₁ не зависят от случайных величин ξ(s) c s < t₁ . Таким образом, марковские процессы (процессы без последействия) характеризуются тем, что вероятностные свойства процесса в момент t ≥ t₁ определяются состоянием в момент t₁ и не зависят от состояний процесса до момента t₁.

Рассмотрим вначале марковские процессы с непрерывным временем и с конечным или счётным множеством состояний X = {x₁, x₂, …}. Подробнее всего рассмотрим случай конечного множества состояний, так как он отличается от цепей Маркова лишь тем, что здесь время изменяется непрерывно и переход системы из одного состояния x_i в другое x_j происходит в любой момент времени. Введём вероятности перехода p_{i j} (s, t):

p_{i j} (s, t) = P{ ξ(t) = x_j | ξ(s) = x_i}, p_{i j} (s, t) ≥ 0. (2.2.1)

Очевидно,

, s ≤ t, p_{i i} (t, t) = 1, p_{i j} (t, t) = 0, i ≠ j. (2.2.2)

Обозначим через a_i начальное распределение вероятностей, t = t₀,

a_i ≥ 0 , , (2.2.3)

а через p _j (t) – абсолютную вероятность, т. е. вероятность того, что система будет в состоянии x_j в момент t, t ≥ t₀ . В силу формулы полной вероятности очевидны следующие равенства:

p _j (t) = , (2.2.4)

p_{i j} (s, t) = . (2.2.5)

Теорема 2.1. Пусть переходные вероятности p_{i j} (s, t) имеют частные производные по t и s. Тогда при s ≤ t

(2.2.6)

(2.2.7)

где

A_{i k} (t) = A_{i k} (t) ≥ 0, i ≠ k, A_{k k} (t) ≤ 0,

. (2.2.8)

Уравнения (2.2.6) и (2.2.7) называются прямой, а уравнения (2.2.8) обратной системой уравнений Колмогорова.

Физический смысл величин A_{i j} (t)dt есть вероятность перехода из состо-яния x_i в состояние x_j за время от t до t +dt. Если функции A_{i j} (t) непрерывны, то функции p_{i j} (s, t) представляют единственное решение системы уравнений (2.2.6), удовлетворяющее начальным условиям p_{i i} (s, s) = 1, p_{i j} (s, s) = 0, i ≠ j. Таким образом, рассматриваемый марковский процесс полностью определяется заданием функций A_{i j} (t). Нетрудно показать также, что если заданы любые непрерывные функции A_{i j} (t), удовлетворяющие условиям, налагаемым на них в (2.2.8), то решение p_{i j} (s, t) системы (2.2.6) при начальных условиях p_{i i} (s, s) = 1, p_{i j} (s, s) = 0, i ≠ j, будет неотрицательным (p_{i j} (s, t) ≥ 0), справедливо равенство (2.2.5), так что p_{i j} (s, t) будут определять некоторый марковский процесс.

Основываясь на прямой системе уравнений Колмогорова, получим дифференциальные уравнения для абсолютных вероятностей p_i (t). Если a_i, задаваемые (2.2.3) – начальное распределение вероятностей, то заменяя в (2.2.4) j на i и дифференцируя это соотношение по t, используя (2.2.6), а затем снова преобразованное (2.2.4), получаем систему уравнений

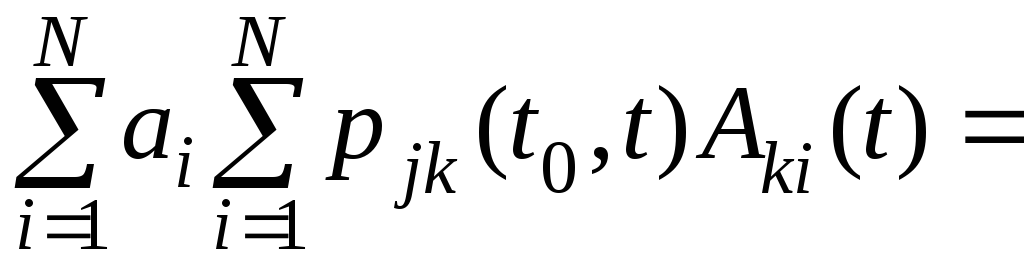
. (2.2.9)

Начальные условия для этой системы таковы: p_i (t₀) = a_i, i = 1, …, N.

Для однородного марковского процесса вероятности перехода p_{i j} (s, t) зависят лишь от разности t – s. В этом случае, согласно определению (2.2.8) A_{i j} – константы, и система уравнений (2.2.6) приобретает вид

(2.2.10)

Замечание 2.5. В случае счётного числа состояний X =(x₁, x₂, …) прямая и обратная системы уравнений Колмогорова (2.2.6) – (2.2.8) остаются справедливыми, но для их обоснования надо дополнительно требовать равномерной сходимости соответствующих рядов.

П р и м е р ы.

1. Двусторонняя реакция. Система может находится в двух состояниях: x₁ – нераспавшаяся частица, x₂ – распавшаяся частица. Возможен как процесс распада с вероятностью α dt, так и процесс восстановления с вероятностью βdt время dt. В этом случае A₁₂ = α, A₂₁ = β, а тогда A₁₁ = – α, A₂₂ = – β. Уравнения (2.2.9) дают

(2.2.11)

Пусть задано начальное распределение вероятностей состояний, например

a₁ = 1, a₂ = 0. (2.2.12)

Тогда легко получить решения системы уравнений (2.2.11) и показать, что при t → ∞ существуют предельные, не зависящие от времени вероятности p₁(t) → β/( α + β), p₂(t) → α /(α + β), т. е. процесс эргодичен.

2. Пуассоновский поток требований. Пусть на некоторую систему обслуживания поступают требования так, что ξ(t) – число требований за время t – образует однородный марковский процесс со счётным числом состояний x_i = 0, 1, 2, … . Из состояния i система непосредственно может перейти только в состояние i+1, i = 0, 1, 2, … . Таким образом, A_i,i+1 = α, остальные A_{i j} = 0 при i ≠ j и согласно (2.2.8) A_{i i} = – α. Для абсолютных вероятностей p_j (t), то есть вероятностей того, что за время t поступит j требований, имеем бесконечную систему уравнений (2.2.9)

(2.2.13)

с начальными условиями

p₀(0) = 1, p_i (0) = 0, i = 1, 2, … . (2.2.14)

Перепишем систему (2.2.13) подробнее:

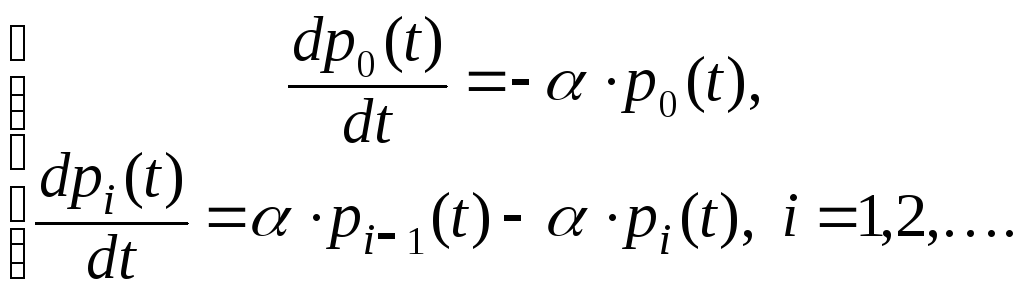(2.2.15)

Эта система легко решается и при заданных начальных условиях её решения:

(2.2.16)

то есть рассмотренный поток требований является пуассоновским.

3. Пусть однородный марковский процесс обладает свойством эргодичности: p_{i j} (t) → p_j при t → ∞. Тогда, как видно из системы уравнений (2.2.13), стационарные вероятности p_j удовлетворяют системе уравнений

= 0, k = 1, 2, …, (2.2.17)

кроме того выполнено условие нормировки .

Пусть, например, A_{i,i +1} = A, A_{i +1, i} = B, B > A, A₁₁ = – A, A_{i i} = – (A + B), i > 1, A_{i j} = 0 для других i и j. Тогда указанная выше система уравнений имеет вид

Bp₂ – Ap₁ = 1, k = 1,

Bp_{k +1} – Ap_k = Bp_k – Ap_{k –1}, k = 2, 3, … . (2.2.18)

Отсюда получаем p_k = (A/B)^{k –1}p₁, а условие нормировки даёт p₁ = 1 – A/B. Таким образом, стационарные вероятности в этом случае равны

p_k = (2.2.19)

Теперь рассмотрим марковские процессы ξ(t) с непрерывным множеством состояний.

Наиболее интересным и важным с точки зрения приложений является случай процессов, у которых n-мерная функция распределения с любым n имеет плотность распределения вероятностей. Конкретнее: пусть ξ(t) – случайный процесс, t T, и пусть при каждом наборе моментов времени t₁, t₂, …, t_n  T n-мерная случайная величина (ξ(t₁), ξ(t₂), …, ξ(t_n)) имеет n-мерную плотность вероятности p_n (t₁, x₁; t₂, x₂; …, t_n, x_n). Эта плотность обладает двумя очевидными свойствами:

1) p_n (t₁, x₁; t₂, x₂; …, t_n, x_n) симметрична относительно перестановок любых пар аргументов (t_i, x_i), ибо p_n (t₁, x₁; t₂, x₂; …, t_n, x_n)dx₁…dx_n выражает вероятность совместного осуществления событий x_i ≤ ξ(t_i) ≤ x_i + dx_i , i = 1, …, n и стало быть не зависит от порядка их перечисления;

2) все конечномерные плотности p_n для различных n должны бы согласованы в том смысле, что плотность любого k-мерного распределения при k < n определяется с помощью n-мерного распределения:

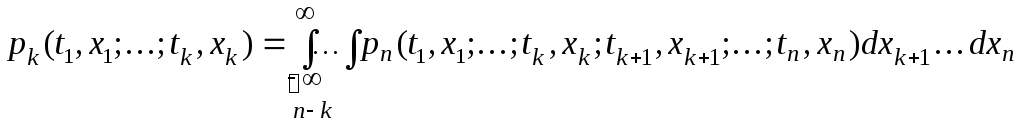.(2.2.20)

Согласно определению плотности условной вероятности (см. §2 ч.I Практикума) p_n (t₁, x₁; t₂, x₂; …, t_n, x_n) =

= p_{n –1} (t₁, x₁; t₂, x₂; …, t_{n –1} , x_{n –1} ) q_n (t_n, x_n | t₁, x₁; t₂, x₂; …, t_{n –1} , x_{n –1} ).

Так как свойство марковости процесса означает, что вероятностные свойства процесса в момент t_n определяются состоянием в момент t_{n –1} и не зависят от протекания процесса в предшествующие моменты времени, то

q_n (t_n, x_n | t₁, x₁; t₂, x₂; …, t_{n –1} , x_{n –1} ) = q_n (t_n, x_n | t_{n –1} , x_{n –1} ). (2.2.21)

Условную вероятность q (t, x | τ , y ) называют переходной плотностью вероятности.

Подставляя (2.2.21) в определение плотности условной вероятности, получаем

p_n (t₁, x₁; t₂, x₂; …, t_n, x_n) = p_{n –1} (t₁, x₁; t₂, x₂; …, t_{n –1} , x_{n –1} ) q_n (t_n, x_n | t_{n –1} , x_{n –1} ).

Применяя эту формулу последовательно для n, n – 1, …, 2 получим

p_n (t₁, x₁; t₂, x₂; …, t_n, x_n) = p₁(t₁, x₁)q(t₂, x₂ | t₁, x₁)… q_n (t_n, x_n | t_{n –1} , x_{n –1} ). (2.2.22)

Полученное равенство означает, что для задания n-мерной плотности вероятности марковского процесса достаточно знать лишь две функции: одномерную плотность p₁(t₁, x₁) и переходную плотность вероятности q (t, x | τ , y ).

Основным в теории непрерывных марковских процессов является уравнение Смолуховского (оно также называется уравнением Колмогорова – Чепмена – см. (2.1.6) и замечание 2.4):

q (t, x | t₀ , x₀ ) = (2.2.23)

для любых трёх моментов времени t₀ < τ < t, t₀, τ, t  T.

Для однородного марковского процесса переходная плотность вероятности зависит лишь от разности моментов времени q (t, x |τ , y ) = q (x |t –τ , y ).

Уравнение Смолуховского в этом случае принимает вид

q (x |t – t₀ , x₀ ) = . (2.2.24)

В теории марковских процессов многие результаты можно и удобно получать при рассмотрении математической модели, описывающей блуждание частицы под действием случайных толчков (размерность пространства при этом может широко варьироваться). Поскольку такая модель (с определёнными дополнениями и изменениями) имеет широкое применение в физических и технических приложениях, ограничимся в дальнейшем её рассмотрением.

В уравнении Смолуховского промежуточный момент времени τ может быть выбран между t и t₀ произвольным образом. Возьмём его весьма близким к t, положив τ = t – Δ , и сделаем предположения о существовании следующих пределов.

Во-первых, предполагаем, что

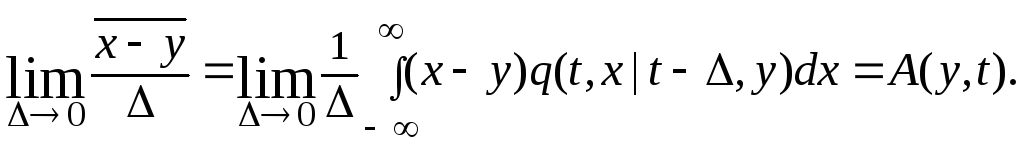(2.2.25)

Смысл этого выражения очевиден: –это условное среднее значения перемещения за время Δ из фиксированной точки y, так что A(y, t) – это средняя скорость изменения состояния в момент t в точке y (так называемый коэффициент сноса).

Во-вторых, допускаем, что

= B(y, t). (2.2.26)

Величина есть мера разброса возможных конечных точек x относительно фиксированной исходной точки y. Предполагается таким образом, что этот разброс при удалении от момента t – Δ на Δ растёт по диффузионному

Условия (2.2.25) и (2.2.26) задают т. н. диффузионное приближение, которого достаточно для описания марковского процесса с непрерывным множеством возможных состояний с помощью упрощённого приёма: время t и множество состояний x разбиваются на весьма малые промежутки Δ t и Δ x, составляются уравнения для марковской последовательности, а затем делается переход к пределу при Δ t → 0 и Δ x → 0. Коэффициент B(y, t), точнее B/2, называется коэффициентом диффузии (и таковым и является в физических приложениях).

Возвращаясь к заявленной в начале этого подраздела модели случайных блужданий под действием случайных толчков, что является частным проявлением движения рассматриваемой системы под действием случайной силы, можно показать, что B(y, t) характеризует интенсивность толчков.

В-третьих, предположим, что

= 0. (2.2.27)

Таким образом, предполагается, что вероятность больших изменений |x – y | достаточно быстро стремится к нулю при Δ → 0, так быстро, что убывает быстрее Δ. Именно это требование и позволяет рассматривать x в системе, подвергающейся действию случайных толчков, как непрерывно меняющуюся величину, т. е. как среднее за время, гораздо большее промежутка между двумя толчками. Эти выводы неприменимы, следовательно, к промежуткам времени, малым по сравнению со временем между толчками.

Н а п р и м е р, вероятность соударения молекул газа за время τ, малое по сравнению со временем свободного пробега θ, есть 1 – e ^–τ/θ ≈ τ/θ . При соударении скорость молекулы u (которая и представляет собой в этом случае величину x, описывающую состояние молекулы) меняется в среднем на конечную величину Δu = ± a. Следовательно, для τ « θ и условие не выполнено.

Принимая условие (2.2.27), мы ограничиваемся марковскими процессами, у которых непрерывно не только множество возможных значений, но и само протекание процесса во времени, т. е. смена состояний происходит непрерывно (в вероятностном смысле), без скачков. Такие марковские процессы часто называют диффузионными.

Для таких марковских процессов, преобразуя, с учётом предположений (2.2.25) – (2.2.27), уравнение Смолуховского (2.2.23), получаем

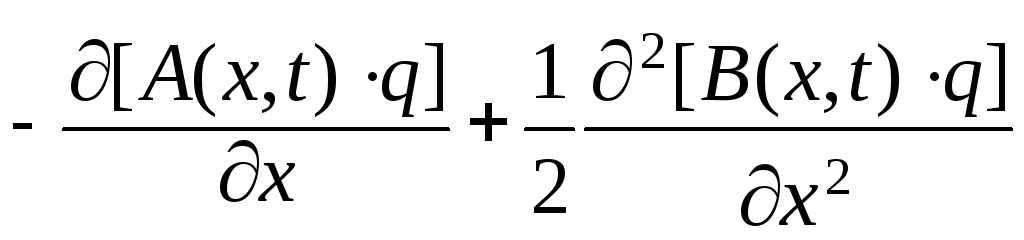=. (2.2.28)

Это параболическое уравнение (типа диффузионного) называют уравнением Эйнштейна – Фоккера – Планка или прямым (первым) уравнением Колмогорова. По самому смыслу переходной вероятности, решение этого уравнения должно быть не отрицательным (q (t, x | t₀ , x₀ ) ≥ 0) и нормированным на единицу (и) и удовлетворять начальному условию

q (t, x | t₀ , x₀ = δ(x – x₀). (2.2.29)

Однако, это же решение q (t, x | t₀ , x₀ ), удовлетворяющее тем же вышеприведённым условиям, удовлетворяет ещё одному уравнению

=, (2.2.30)

называемому обратным (вторым) уравнением Колмогорова. Уравнение (2.2.30) следует решать в обратную сторону по времени, для t₀ ≤ t.

Замечание 2.6. Наглядно уравнение (2.2.28) можно истолковать следующим образом. В момент t₀ из точки x₀ выходит большое число (ансамбль) частиц, движущихся независимо друг от друга. Их концентрация (относительная «частота») в точке x в момент t будет q (t, x | t₀ , x₀). Поток частиц Q складывается из систематического («гидродинамического») потока Aq, где A – скорость систематического движения в точке x в момент t, и из диффузионного потока –, гдеB/2 – коэффициент диффузии: Q = Aq – .

Тогда уравнение Фоккера – Планка – это просто уравнение непрерывности:

,

выражающее сохранения числа частиц.

Пусть в начальный момент t₀ задана плотность распределения вероятности p(t₀, x) случайной величины ξ(t₀). Тогда двумерная плотность распределения вероятности для произвольного момента времени t ≥ t₀ и начального момента t₀ равна

p₂(t, x; t₀, x₀) = p(t₀, x₀) q (t, x | t₀ , x₀), (2.2.31)

а одномерная плотность случайного процесса ξ(t) для момента t равна

p₁(t, x) = . (2.2.32)

Если теперь уравнение (2.2.28) Эйнштейна – Фоккера – Планка умножить на p(t₀, x₀) и проинтегрировать по x₀, то в силу (2.2.32) найдём, что плотность p₁(t, x) удовлетворяет тому же уравнению

=. (2.2.33)

Решение этого уравнения должно удовлетворять условиям

p₁(t, x) ≥ 0; ;p₁(t, x= p(t₀, x).

П р и м е р ы.

1. Пусть марковский процесс однороден по времени, т. е. q (t, x | t₀ , x₀) = = q (x | t – t₀ , x₀). В этом случае в условиях (2.2.25), (2.2.26) функции A и B не зависят от t. Пусть, кроме того, одномерная плотность p₁ также не зависит от времени (стационарный марковский процесс). Тогда уравнение (2.2.33) записывается в виде

d/dx{A(x)p₁(x) – 1/2∙ d/dx[B(x) p₁(x)]} = 0. (2.2.34)

Если на границах изменения x (т. е. в области значений процесса ξ(t)) поток Ap₁ – 1/2∙ d/dx(B p₁) равен нулю, то в силу (2.2.34) он равен нулю всюду

A(x)p₁(x) – 1/2∙ d/dx[B(x) p₁(x)] = 0. (2.2.35)

Интегрируя это дифференциальное уравнение (для этого полагаем υ = B p₁), получим

p₁(x) = (2.2.36)

где C – постоянная определяемая из условий нормировки плотности.

Физическим примером, в котором существует стационарное распределение p₁(x), является броуновское движение частиц над отражающей границей при наличии силы тяжести. Здесь A = – mg. Ясно, что на отражающей границе выполнено условие обращения потока в нуль, так что уравнение (2.2.35) имеет место. Выражение (2.2.36) с постоянными A и B даёт

p₁(x) ==

т. е. получили барометрическую формулу, причём B = 2kT, k – постоянная Больцмана, T – абсолютная температура.

2. Рассмотрим марковский процесс, однородный по координате, т. е. q(t, x | t₀ , x₀) = q(t, x – x₀ | t₀). В этом случае в условиях (2.2.25), (2.2.26) функции A и B зависят лишь от t и уравнение (2.2.33) имеет вид

. (2.2.37)

С помощью замены переменных (t, x) → (τ, y) по формулам

y = x – x₀ – , τ =,

приходим к уравнению теплопроводности

.

Его решение, удовлетворяющее условиям нормировки и начальным условиям (2.2.29), имеет вид

q(τ, y) = (2πτ) ^{– 1/2}exp(– y²/2τ),

или в старых переменных

q(t, x – x₀ | t₀) = (2π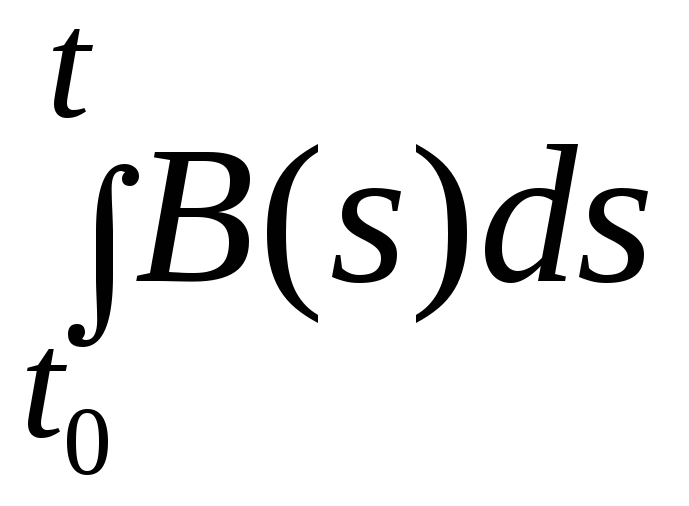) ^{– 1/2}exp{– ( x – x₀ – )²/2}. (2.2.38)

Пусть, в частности, A(t) = 0, а B(t) = B – const. Тогда

q(t, x – x₀ | t₀) = .

Отсюда среднее смещение частицы в броуновском движении равно нулю, а средний квадрат смещения равен B(t – t₀), то есть растёт пропорционально времени (результат впервые получен Эйнштейном).

И в заключение этого раздела немного о скачкообразных марковских процессах, т. е. процессах, для которых не выполняется ограничение (2.2.27), но и цепями Маркова они считаться не могут. Пример такого процесса приводился ранее: при столкновении молекул газа скорость отдельной молекулы меняется скачком, но множество возможных значений скорости после удара непрерывно. Кроме соударений микрочастиц (молекул, атомов, электронов и т. д.) в эту схему укладываются и квантовые переходы, и некоторые импульсные процессы.

Обозначим a(t, x) – вероятность скачка (из состояния x в начальный момент скачка t) и φ(z | t, x) – плотность условной вероятности значений z, принимаемых в результате скачка (зависимость этих величин не только от предшествующего значения x, но и от времени t, делает процесс ξ(t) уже нестационарным).

Потребуем также выполнения, с точностью до первого порядка относительно Δt соотношения

q(t + Δt, z|t, x) ≈ [1 – a(t, x) Δt]δ(z – x) + a(t, x) Δt∙ φ(z | t, x). (2.2.39)

В предположении (2.2.39) и при некоторых дополнительных требованиях (непрерывности a и φ как функций t и ограниченности a на любом конечном интервале t) из уравнения Смолуховского вытекает прямое интегро-дифференциальное уравнение Колмогорова – Феллера

= – a(t, x)∙q(t, x | t₀, x₀) + ∫a(t, y)∙φ(x | t, y)∙q(t, y | t₀, x₀)dy. ( 2.2.40)

Справедливо и обратное (t₀ > t) уравнение Колмогорова – Феллера

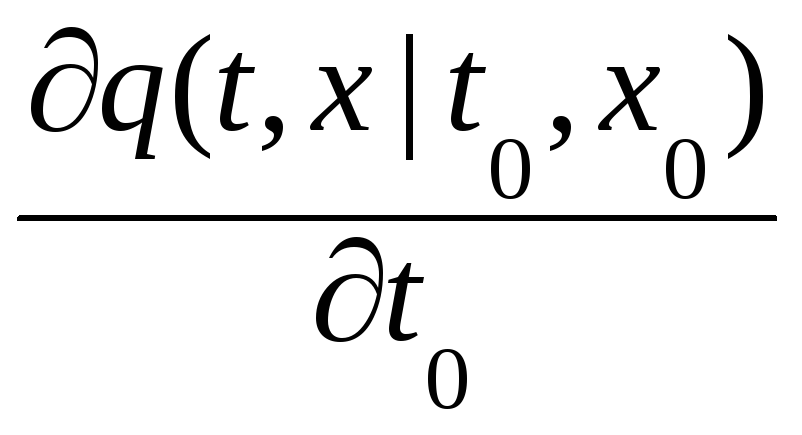= a(t₀, x₀)[ q(t, x | t₀, x₀) – ∫φ(y |t₀, x₀)∙q(t, x| t₀, y)dy]. (2.2.41)

При начальном условии

q(t₀, x | t₀, x₀) = δ(x – x₀)

оба уравнения имеют единственное решение, причём одно и то же.

В общем случае сочетания в едином процессе диффузионной и скачкообразной составляющих интегро-дифференциальные уравнения Колмогорова – Феллера по прежнему верны, но к их правой части добавляется правая часть первого или второго уравнений Колмогорова (Фоккера – Планка).

Уравнение Колмогорова – Феллера ( 2.2.40) можно записать также в виде классического кинетического уравнения Больцмана, основного уравнения кинетической теории газов. Введём плотность вероятностей скачка в момент времени t из состояния y в состояние x:

u (y | t, x) = a(t, y)∙φ(x | t, y). (2.2.42)

Справедливость этого равенства вытекает из следующего ряда соображений: a(t, y)∙dt – вероятность скачка из y куда-нибудь (то есть вероятность того, что в интервале времени от t до t +dt в y был скачок), а φ(x | t, y)dx – условная вероятность того, что при наличии скачка процесс перешёл в (x, x + dx). Произведение этих вероятностей представляет собой условную вероятность u, как она определена выше. Интегрируя (2.2.42) по всем x, учитывая при этом, что ∫φ(x | t, y)∙d x = 1, и меняя местами переменные (x ↔ y), получаем

∫u (y | t, x)dy = a(t, x). (2.2.43)

Если подставить (2.2.43) в первый член правой части (2.2.40), а (2.2.42) – во второй, то уравнение (2.2.40) примет вид

= – q(t, x |t₀, x₀) ∫u (y |t, x)dy + ∫q(t, y |t₀, x₀)u (y |t, x)dy. (2.2.43)

Это и есть уравнение Больцмана (для одномерного процесса). Из него хорошо видно, что это, по существу, уравнение баланса: скорость изменения q (например, концентрации частиц в точке x) равна разности двух обусловленых скачками ежесекундных потоков – из x в какое либо другое состояние и из всех других состояний в x.