4. Стационарность и однородность случайных функций;

эргодичность

Стационарность случайных процессов

Случайный процесс ξ(t) называют стационарным в узком (строгом) смысле, если все конечномерные функции распределения вероятностей любого порядка инвариантны относительно сдвига по времени, т. е. при любых n и t₀ справедливо равенство

F_n (x₁, …, x_n; t₁ – t₀, …, t_n – t₀) = F_n (x₁, …, x_n; t₁, …, t_n). (1.4.1)

У стационарного в узком смысле процесса математическое ожидание и дисперсия – постоянные, т. е. m_ξ (t) = m_ξ = const; D_ξ = K_ξ (t, t) = const, а корреляционная функция зависит лишь от разности своих аргументов: K_ξ (t, t') =

= K_ξ (τ), где τ = t' – t.

Если для процесса ξ(t) выполняются лишь перечисленные условия, а равенство (1.4.1), начиная с некоторого значения n, не выполняется, то этот случайный процесс называют стационарным в широком смысле.

Из стационарности в узком смысле, очевидно, следует стационарность в широком смысле, но не наоборот. Для нормальных стационарных процессов оба понятия стационарности совпадают. Следует также отметить, что сумма двух нестационарных процессов может оказаться стационарным процессом.

Для стационарного в широком смысле процесса ξ(t) справедливо:

K_ξ(–τ) = K_ξ(τ); K_ξ(0) = D_ξ ; | K_ξ(τ) |≤ K_ξ(0); . (1.4.2)

Два случайных процесса ξ(t) и η(t) называются совместно стационарно связанными в узком смысле, если их совместные функции распределения вероятностей любого порядка инвариантны относительно сдвига по времени:

F_n (x₁, …, x_n; y₁, …, y_m; t₁ – t₀, …, t_n – t₀; t'₁ – t₀, …, t'_m – t₀) =

= F_n (x₁, …, x_n; y₁, …, y_m; t₁, …, t_n; t₁, …, t_m). (1.4.3)

Надо отметить, что если каждый из процессов ξ(t) и η(t) является стационарным, то отсюда вовсе не следует, что они будут стационарно связанными в узком смысле.

Два случайных процесса ξ(t) и η(t) называются стационарно связанными в широком смысле, если их взаимная ковариационная функция (т.е. и корреляционная функция тоже) инвариантна относительно сдвига по времени:

R_ξη (t₁, t₂) = M{ ξ(t₁)η(t₂)} = M{ ξ(t₁ – t₁)η(t₂ – t₁)} = R_ξη (τ), τ = t₂ – t₁. (1.4.4)

Отметим, что если каждый из процессов ξ(t) и η(t) является стационарным в широком смысле, то отсюда вовсе не следует, что они являются стационарно связанными в широком смысле.

Помимо указанных двух основных определений стационарности, встречаются и другие понятия стационарности:

• Случайный процесс ξ(t) называется стационарным порядка k, если равенство (1.4.1) выполняется не для любых n, а только при n ≤ k.

• Случайный процесс ξ(t) называется асимптотически стационарным в узком смысле, если  .

• Случайный процесс ξ(t) называется стационарным в узком смысле на конечном интервале, если равенство (1.4.1) выполняется только для всех временных точек этого интервала. Этот процесс будет стационарным в широком смысле на конечном интервале, если для всех временных точек этого интервала он имеет постоянное математическое ожидание и корреляционную функцию, инвариантную относительно сдвига по времени.

• Случайный процесс со стационарными в узком смысле приращениями – процесс, у которого приращения, т.е. разность ξ(t + τ) – ξ(t) для каждого фиксированного τ, есть стационарный в узком смысле процесс. Если эти приращения – стационарный в широком смысле процесс, то ξ(t) – случайный процесс со стационарными в широком смысле приращениями.

• Случайный процесс ξ(t) называется периодически стационарным или циклостационарным в узком смысле с периодом T, если равенство (1.4.1) выполняется только при t₀ = mT, m = 1, 2, … . Случайный процесс ξ(t) называется периодически стационарным в широком смысле с периодом T, если для любых целых чисел k и m выполняются равенства

M{ ξ(t + kT)} = M{ ξ(t)} = m_ξ(t), K_ξ (t + kT, t' + mT) = K_ξ (t, t'). (1.4.4)

При этом следует отметить, что несмотря на наличие термина «стационарный», три последние группы случайных процессов стационарными не являются.

Однородность случайных полей

Приведённые определения распространяются и на случайные поля. Однородность случайного поля является аналогом стационарности случайного процесса. Случайное поле ξ() называетсяоднородным, если его плотности вероятности любого порядка не меняются при произвольном сдвиге начала координат, т. е.

. (1.4.5)

Физически однородность поля указывает на то, что в любой точке пространства поле ведёт себя «в среднем» одинаково. Если равенство (1.4.5) не выполняется, то поле являетсянеоднородным.

В более общем случае поле определено как функция координат пространства и времениt, т. е. ξ(,t). В таком случае к полю применимо понятие стационарности: случайное поле называется стационарным (во времени) в узком смысле, если его плотности не меняются при изменении начала отсчета времени (что относится как к однородным, так и неоднородным полям). Для стационарного однородного поля должно выполняться

, (1.4.6)

где ;Δτ_j = t_j – t₀ , j = 1, …, n. В частности, поместив начало отсчёта в точку (₁, t₁), получаем для одномерной и двумерной плотности вероятности

(1.4.7)

(1.4.8)

где .

Случайное поле называется однородным в широком смысле слова, если его математическое ожидание не зависит от координат пространства, а пространственная корреляционная функция является функцией только разности аргументов, т. е. для случайного поля ξ()

, (1.4.9)

а для случайного поля ξ(,t) будем иметь . Стационарность в широком смысле неоднородного поля порождает корреляционную функцию , где τ = t₂ – t₁, а стационарность однородного поля –.

Если случайное поле однородно в узком смысле, то оно однородно и в широком смысле. Обратное утверждение в общем случае несправедливо. Лишь для гауссовских случайных полей понятие однородности в узком и широком смысле совпадают.

Для однородных полей имеем:

математическое ожидание однородного поля

m_ξ = , (1.4.10)

дисперсия однородного поля

D_ξ = , (1.4.11)

корреляционная функция однородного поля (при отсутствии временной зависимости)

. (1.4.12)

Для однородных нестационарных полей корреляционная функция зависит от моментов t₁ и t₂ замеров поля в точках и , т. е., а для однородных стационарных полей – только от разности этих моментов τ = t₂ – t₁: . Корреляционная функция в нуле во всех этих случаях не зависит от времени и равна дисперсии однородного поля: D_ξ =.

Замечание 1.4.1. Так как , то пространственная корреляционная функцияв отличии от корреляционной функцииK_ξ(τ) случайного процесса – функция многих переменных

Эргодичность случайных процессов и полей

Параметры и характеристики случайных функций, при наличии зависимости от времени, можно определять двояко: путём усреднения по большому числу реализаций, либо путём усреднения по отрезку времени достаточной продолжительности одной реализации. При совпадении каких-либо характеристик в результате таких методов определения, говорят об эргодичности случайных функций по этим характеристикам.

Оказывается, что нестационарные случайные функции свойством эргодичности не обладают, т. е. это свойство присуще только стационарным процессам и полям, причём не всем. Таким образом например, для стационарных эргодических случайных процессов справедливы следующие оценки основных характеристик:

математическое ожидание стационарного эргодического процесса ξ(t)

m_ξ =; (1.4.13)

дисперсия стационарного эргодического процесса ξ(t)

D_ξ = , (1.4.14)

корреляционная функция стационарного эргодического процесса ξ(t)

K_ξ (τ) =. (1.4.15)

На практике временной интервал осреднения T берут конечным, но по возможности большим.

Необходимым и достаточным условием зргодичности процесса ξ(t) является выполнение условия

. (1.4.16)

Достаточно условие K_ξ (t, t') → 0 при |t – t' | → ∞.

Аналогично обстоит дело и со случайными полями. Например, для однородного поля в соответствующих выражениях типа (13) – (15) осреднение по времени надо заменить осреднением по достаточно большой области пространства.

Итак, стационарный процесс ξ(t) называется эргодическим в строгом смысле, если с вероятностью единица все его вероятностные характеристики могут быть получены по одной реализации процесса. Это определение в полной мере относится и к однородному случайному полю ξ().

На практике часто интересуются не всеми, а только отдельными характеристиками случайных функций (в частности, математическим ожиданием, корреляционной функцией и одномерной функцией распределения или плотности вероятности). Ясно, что случайная функция может быть эргодической относительно одной характеристики (параметра) и неэргодическим для других. В вязи с этим введём понятие эргодичности отдельных основных параметров случайной функции. Сделаем это на более простом примере стационарной случайной функции, т. е. осреднение единственной реализации будет проводиться по времени, в соответствии с соотношениями (13) – (15). За основу определений эргодичности взят следующий факт: аналоги соответствующих характеристик процесса определяются временным осреднением реализации за конечный интервал времени [0, T] и затем устанавливаются условия, при которых дисперсия получающихся временных средних значений стремится к нулю при T → ∞.

Стационарный случайный процесс ξ(t) обладает эргодическим свойством относительно математического ожидания, т. е. M{ξ(t)} = m_ξ задаётся соотношением (1.4.13) тогда и только тогда, когда выполняется равенство

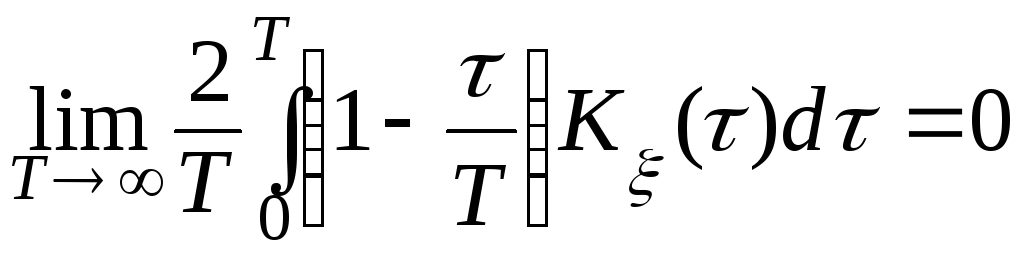. (1.4.17)

Стационарный случайный процесс ξ(t) обладает эргодическим свойством относительно корреляционной функции, т. е. K_ξ (τ) задаётся соотношением (1.4.15) тогда и только тогда, когда выполняется равенство

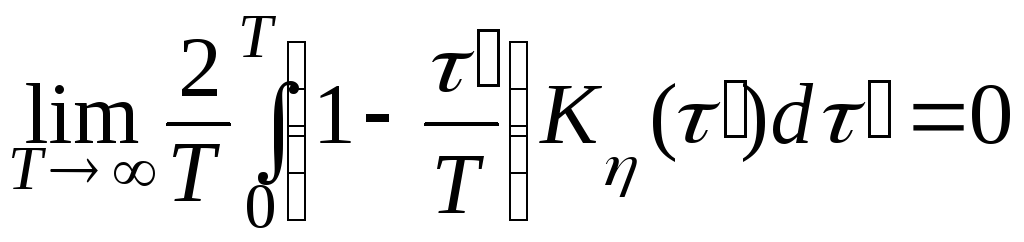, (1.4.18)

где K_η (τ') – корреляционная функция процесса η(t) = ξ(t + τ) ξ(t).

Стационарный случайный процесс ξ(t) обладает эргодическим свойством относительно одномерной функции распределения F₁(x), т. е.

F₁(x) = (1.4.19)

тогда и только тогда, когда выполняется равенство

. (1.4.20)

Заметим, что для выполнения равенства (1.4.17) необходима стационарность процесса ξ(t) лишь в широком смысле, а для выполнения соотношений (1.4.18) и (1.4.20) – стационарность в узком смысле.