3. Представления и преобразования случайных функций

и их характеристик

При выполнении различных преобразований со случайными функциями часто бывает удобно записывать их в комплексном виде.

Комплексной случайной функцией называется случайная функция вида

ζ(t) = ξ(t) + i η(t), (1.3.1)

где ξ(t) и η(t) – действительные случайные функции.

Математическое ожидание, корреляционная функция и дисперсия комплексной случайной функции определяются следующим образом:

m_ζ (t) = m_ξ (t) + i m_η (t); (1.3.2)

K_ζ (t, t’) = M[ξ⁰(t)·]; (1.3.3)

D_ζ (t) = K_ζ (t, t’) = M[|ξ⁰(t)|²]. (1.3.4)

При переходе к комплексным случайным величинам и функциям необходимо определять дисперсию как математическое ожидание квадрата модуля, а корреляционный момент (корреляционная функция) – как математическое ожидание произведения одной центрированной случайной величины (функции) на комплексную сопряжённую центрированной другой.

При прибавлении к случайной функции ξ(t) неслучайного слагаемого φ(t) то же неслучайное слагаемое прибавляется к её математическому ожиданию, а корреляционная функция не меняется.

При умножении случайной функции ξ(t) на неслучайный множитель φ(t) её математическое ожидание умножается на тот же множитель φ(t), а корреляционная функция – на φ(t) φ(t').

Если случайную функцию ξ(t) подвергают некоторому преобразованию A_t , то получается другая случайная функция η(t) = A_t{ξ(t)}.

Преобразование L_t⁽⁰⁾ называется линейным однородным, если

1) - преобразование к сумме может применяться почленно;

2) L_t⁽⁰⁾{c ξ(t)} = c L_t⁽⁰⁾{ξ(t)} – множитель c, не зависящий от аргумента t, по которому производится преобразование, можно вынести за знак преобразования.

Преобразование L_t называется линейным неоднородным, если

L_t{ξ(t)} = L_t⁽⁰⁾{ξ(t)} + φ(t),

где φ(t) – любая функция, никак не связанная с ξ(t).

Если случайная функция η(t) связана со случайной функции ξ(t) линейным преобразованием η(t) = L_t{ξ(t)} то её математическое ожидание m_η (t) получается из m_ξ (t) тем же линейным преобразованием

m_η (t) = L_t{m_ξ (t)}, (1.3.5)

а для нахождения корреляционной функции K_η (t, t') нужно дважды подвергнуть функцию K_ξ (t, t') соответствующему линейному однородному преобразованию, один раз по t, другой раз по t':

K_η (t, t') = L_t⁽⁰⁾{ L_t'⁽⁰⁾{ K_ξ (t, t') }}. (1.3.6)

Каноническим разложением случайной функции ξ(t) называется её представление в виде

ξ(t) = m_ξ (t) + 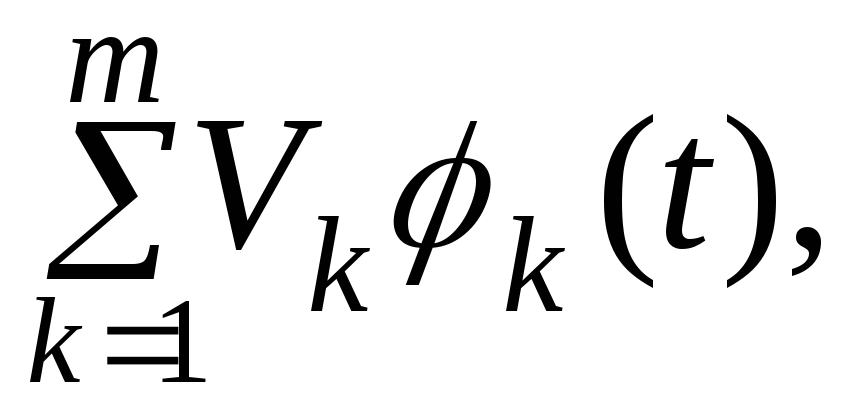(1.3.7)

где V_k (k =1, …, m) – центрированные некоррелированные случайные величины с дисперсиями D_k (k =1, …, m); φ(t) (k =1, …, m) – неслучайные функции (в том числе возможно m = ∞).

Случайные функции V_k (k =1, …, m) называются случайными коэффициентами и должны удовлетворять условиям: MV_k = 0, DV_k = D_k > 0, M(V_k V_j) = 0 при k ≠ j, а функции φ(t) (k =1, …, m) – координатными функциями канонического разложения.

Если случайная функция ξ(t) допускает каноническое разложение (7), то корреляционная функция K_ξ (t, t') выражается суммой вида

K_ξ (t, t') (1.3.8)

где случай а) соответствует каноническому разложению в действительной, а случай б) – в комплексной формах. Разложение вида (8) называется каноническим разложением корреляционной функции. При этом дисперсия случайной функции ξ(t) имеет каноническое разложение

D_ξ (t) = 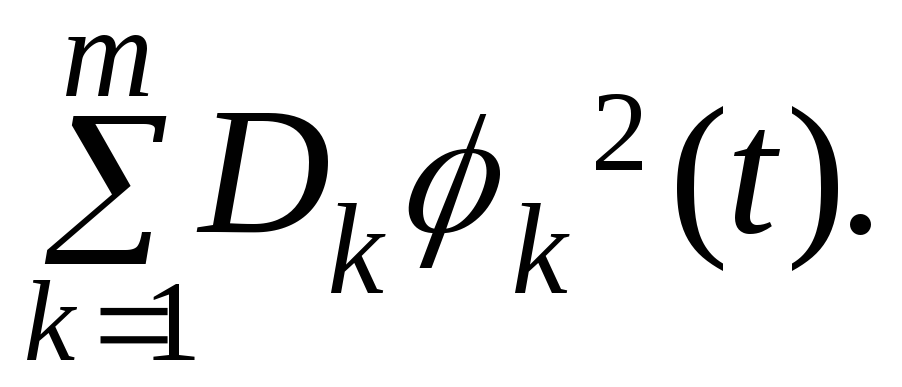(1.3.9)

Вообще, справедливо утверждение, что для существования каноническое разложение случайной функции (7) на некотором интервале (0, T) необходимо и достаточно, чтобы сходился (при m → ∞) на этом интервале положительный ряд (9). Коэффициенты D_k разложения (8) при этом являются дисперсиями случайных величин V_k ,представляющими собой коэффициенты разложения (7).

При линейном преобразовании случайной функции ξ(t), заданной каноническим разложением (7), получается случайная функция η(t) = L_t{ξ(t)} в виде канонического разложения

η(t) = m_η (t) + (1.3.10)

где m_η (t) = L_t{m_ξ (t)}; ψ_k (t) = L_t⁽⁰⁾{φ_k (t)}, т.е. при линейном преобразовании случайной функции, заданной каноническим разложением, её математическое ожидание подвергается тому же линейному преобразованию, а координатные функции – соответствующему линейному однородному.